強く相互作用する電子系の波動関数は電子相関の効果を強く受けている。超伝導相関関数も大きな効果を受けている。
一体問題の波動関数を ψ0 として、ハミルトニアンが H で与えられる系の基底状態の波動関数は、
定数 τ が十分大きいとすると e−τHψ0 と書くことができる。
H には相互作用項が含まれているため容易には扱うことができない。
この波動関数は H を一体の項と相互作用項に分けて H=K+V と書くと
e−ΔτKe−ΔτV … e−ΔτK
e−ΔτVψ0
と近似できる。しかし, この式は取り扱いが難しく負符号が現れる可能性もあるため, 次の波動関数を考える:
e−λmVe−δmK …
e−λ1Ve−δ1Kψ0.
ここで, λj, δj は変分パラメーターである。
我々はさらに近似して小さな m に対して計算を行う。1/m についての外挿を行うことを目標としている。
ψ0としてBCS波動関数を取ると,
BCSの波動関数に対する電子相関の効果を考えることができる。
強く相互作用する電子系における超伝導状態の波動関数として
ψ = e−λKPGψBCS
を考える。
図1 に電子対相関関数の距離依存性を示す [6]。ここで、d電子対の相関関数は次の式により定義される:
Dsc(ℓ) = 〈Δ†(i)Δ(i+ℓ)〉.
ここで, Δ(i) はd波電子対を表す。
図1 によると, 電子対相関関数は ℓ が大きくなってもほぼ一定であり、超伝導状態にあることを示している。
このように強相関電子系においても超伝導状態が存在する。
しかしながら、電子相関相互作用がないBCS関数と比べると大きく相関関数の値は減少している。
これは電子相関のある系における超伝導の特徴を表していると考えられる。
電子相関が超伝導の起源であるにもかかわらず、電子相関の効果により超伝導相関は減少することを表している。
すなわち, 電子相関は超伝導を引き起こすが, 同時に超伝導相関を抑える効果があることを示している。
ここに, 電子相関系における超伝導を考える際の難しさがある(特に数値的研究において)。
超伝導相関を抑える効果は, 主としてGutzwiller因子PGから来ている。
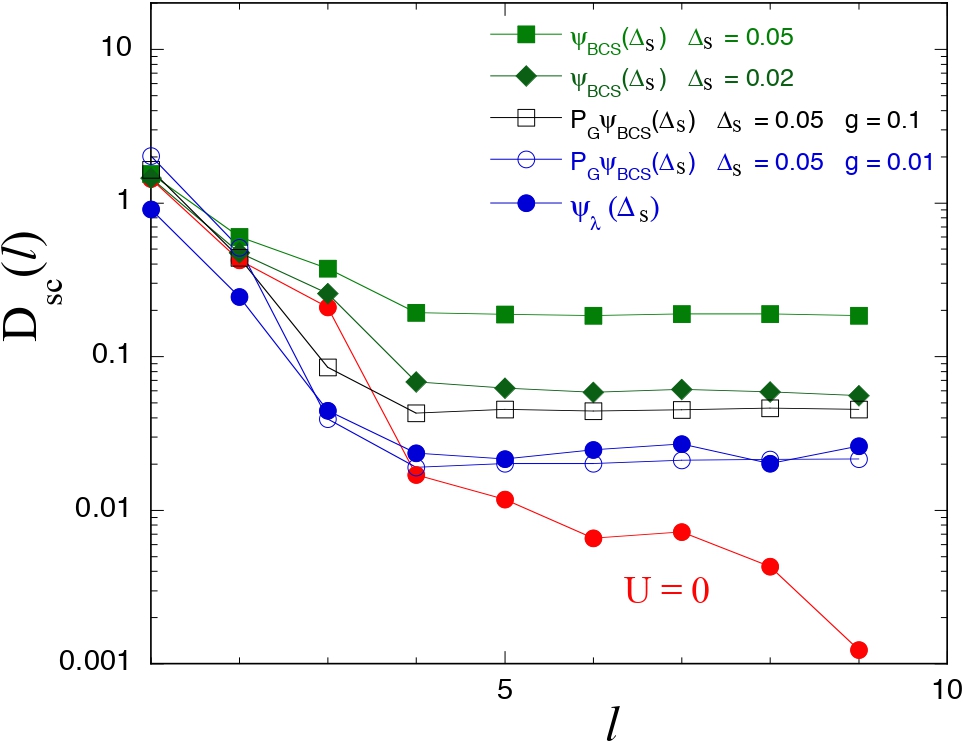
図1. 超伝導相関関数の距離依存性.
10 × 10 格子上におけるd波電子対の相関関数を格子サイトの関数として示した.
電子対をサイト i = (1,1) から ℓ = (1,1), (1,2), (1,3), (1,4), (1,5), (2,5), (3,5),
(4,5), (5,5) へ動かす時の相関関数を表している。
パラメーターは t' = 0, U/t = 18 としている。
参考文献
[1] T. Yanagisawa: J. Phys. Soc. Jpn. 85, 114707 (2016).
[2] T. Yanagisawa: S. Koike and K. Yamaji, J. Phys. Soc. Jpn. 67, 3867 (1998).
[3] T. Yanagisawa: J. Phys. Soc. Jpn. 88, 054702 (2019).
[4] T. Yanagisawa: Phys. Lett. A403, 127382 (2021).
[5] M. Miyazaki and T. Yanagisawa: Phys. Lett. A446, 128276 (2022).
[6] T. Yanagisawa: J. Phys. Soc. Jpn. 94, 074708 (2025).
[7] T. Yanagisawa: High Temperature Materials 1, 10004 (2024).
| |

