銅酸化物高温超伝導体の典型的な相図においては, 伝導のキャリアー数(ホール濃度)が小さい領域には反強磁性相が存在し,
ホール濃度が増えていくと超伝導相が現れ, 超伝導臨界温度が増大して最大となりその後に減少していく。
強相関電子系のモデルに基づいてこの相図を考察してみよう。
電子相関モデルとしては、二次元ハバードモデルを考察する。波動関数としては指数関数型の相関因子により最適化された波動関数を用いる。
この型の波動関数は他の波動関数と比較しても最良の波動関数であり、系統的に改良することができる利点がある。
この波動関数により得られる二次元ハバードモデルの相図を図1に示す。
図1は超伝導および反強磁性の凝縮エネルギーを
ホール濃度(キャリアー濃度)xの関数として示している。
低ドープ領域には反強磁性相が存在し、x < 0.05では反強磁性絶縁体になる。ホール濃度が増えると反強磁性と超伝導の共存状態になり,
ホール濃度が約10%を超えると(x > 0.09)、反強磁性秩序が消えて超伝導状態に移る。
反強磁性から超伝導に移る際には、理論的には反強磁性と超伝導の共存相が存在しうる。
この相図において重要なのは, ホール濃度がゼロの近くには反強磁性絶縁体相が存在することである。
この相においては, ホールが伝導を寄与できずに絶縁体状態となっている。この相が反強磁性絶縁体であるかあるいは
金属的な反強磁性体であるかは, モデルの次近接重なり積分t''の大きさに依存する。
t'= 0のときは反強磁性絶縁体であるが, t'が負である程度の値であると金属的反強磁性となる。
ここで, オンサイトクーロン相互作用Uを U=18t ととっているが, これはホールをドープした時に反強磁性が消えるように大きなUをとった。
ホールがドープされた領域では, Uが0から大きくなっていくと反強磁性相関も大きくなっていくが, Uがさらに大きくなっていくと
反強磁性相関は逆に減少し始める。Uが非常に大きくなると反強磁性秩序は消滅する。そのようなUの値としてU = 18tと取ったが,
波動関数を改良していくと反強磁性が消える臨界値Uの値は減少することがわかっている。
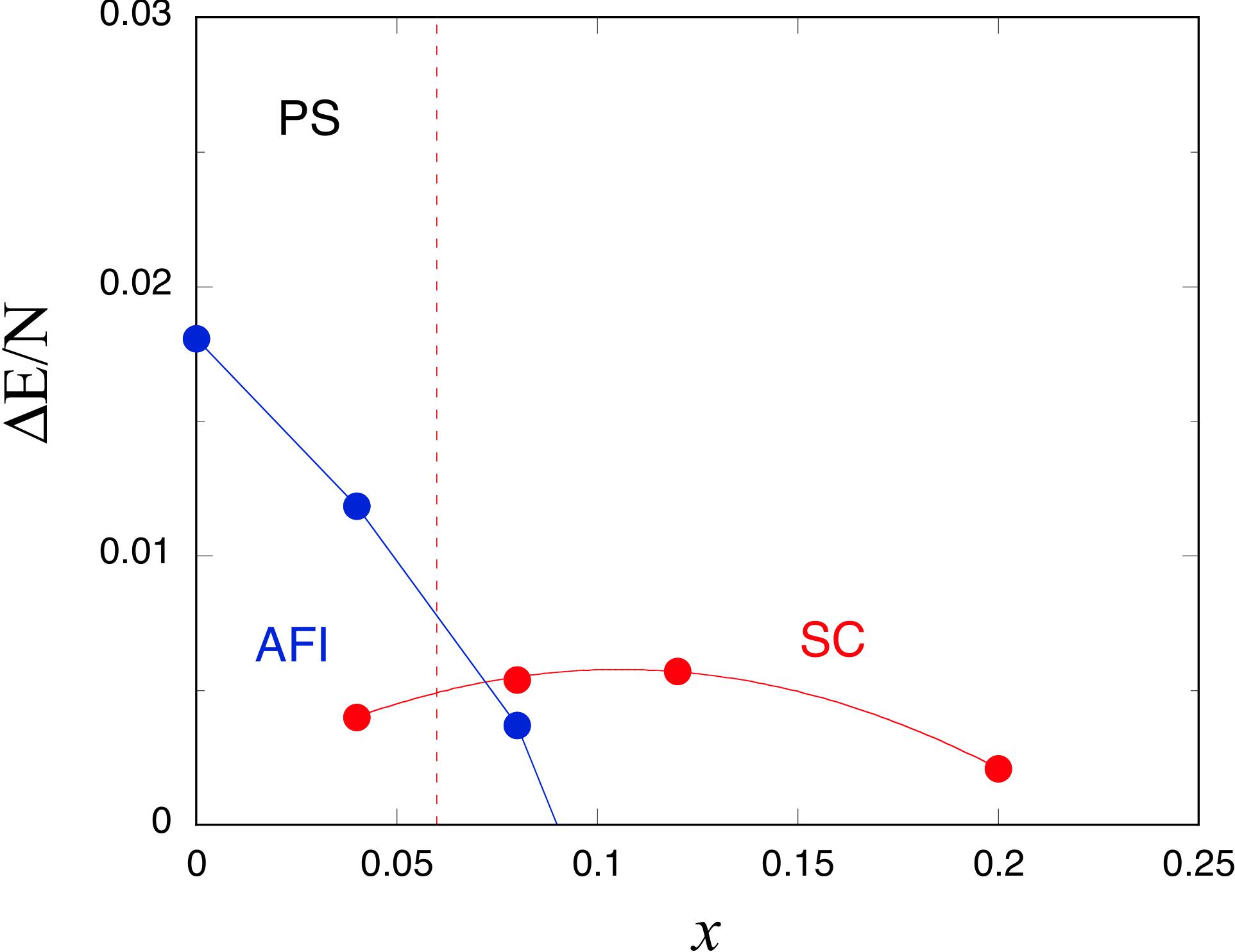
図1. 二次元ハバードモデルの相図.
横軸はホール濃度xを表し, 縦軸は反強磁性および超伝導状態の凝縮エネルギーを表す.
x = 0の近くには反強磁性絶縁体相が存在する。パラメーターはt' = 0, U/t = 18としている。'
超伝導状態の中の電子状態を考えてみよう。実験によると、x = 0.125の近くにはストライプ状の状態が存在すると報告されており、
電荷秩序の存在が以前から指摘されている。電荷秩序が異常金属相の存在と関係がある可能性がある。
ストライプ状態は反強磁性秩序と電荷秩序が共存した状態であるが、t' = 0 の場合は x < 0.1 において既に反強磁性相関が弱いために
電荷秩序のみを持った秩序相が存在するであろう。これはネマテック相であり、実際に電子相関によりこのような状態が安定となり
超伝導と共存すると考えられる。[5]
図2にd波超伝導と電荷秩序が共存する状態のエネルギーを超伝導オーダーパラメーター Δs の関数として示す。[5]
電荷秩序のパラメター ρ が有限の時に, エネルギーが最小になり純粋なd波超伝導よりも安定になる。
Δs がゼロの時の電荷秩序によるエネルギーの下りは小さいが、超伝導と共存することにより,
より凝縮エネルギーが増大して電荷秩序があるネマテック状態が安定化する。
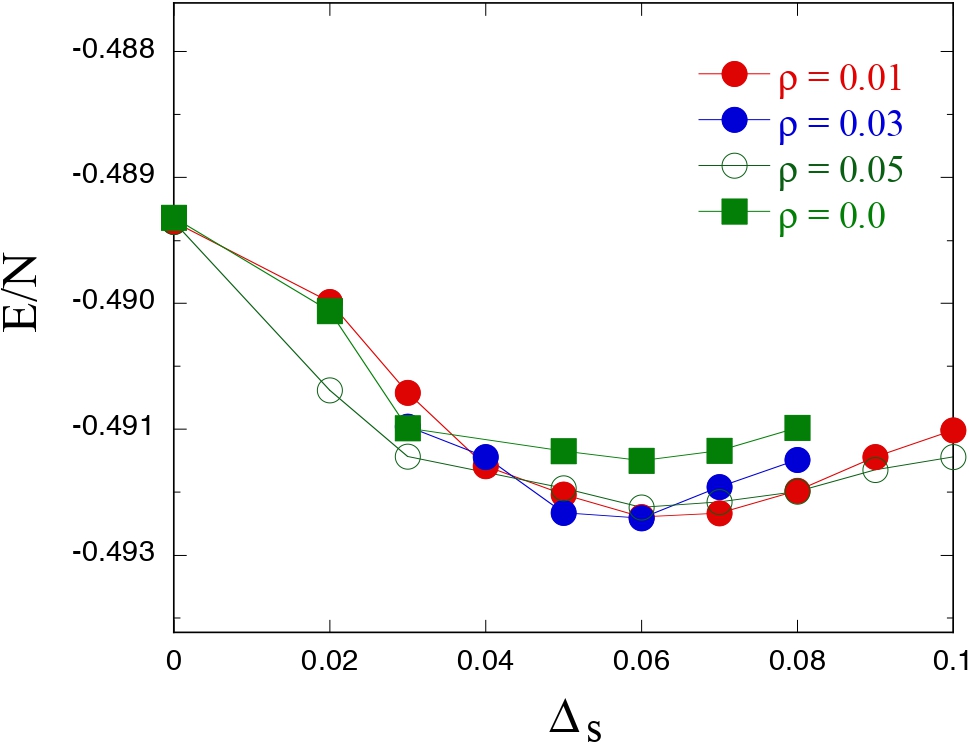
図2. d波と電荷秩序が共存した状態のエネルギー.
横軸は超伝導オーダーパラメーター Δs を表し, 縦軸は単位サイトあたりのエネルギーを表す.
Δ として, 0.0, 0.01, 0.03 および 0.05とした。計算は 16 × 16 格子上で, 電子数 Ne = 228 とおいた。
パラメーターは t' = 0, U/t = 18としている。
参考文献
[1] T. Yanagisawa, J. Phys. Soc. Jpn. 85, 114707 (2016).
[2] T. Yanagisawa, S. Koike and K. Yamaji, J. Phys. Soc. Jpn. 67, 3867 (1998).
[3] T. Yanagisawa: J. Phys. Soc. Jpn. 88, 054702 (2019).
[4] T. Yanagisawa: Phys. Lett. A403, 127382 (2021).
[5] T. Yanagisawa: J. Phys. Soc. Jpn. 94, 074708 (2025).
| |

