The many-body wave function is written in the form
ψ(1) = exp(−λK)PGψ0, where K denotes the kinetic energy part
(non-interacting part) of the Hamiltonian and PG is the Gutzwiller operator
to control the double occupancy with the variational parameter g.
ψ0 indicates a trial wave function which is usually taken as the
Fermi sea, the BCS wave function or the state with some magnetic (or
charge) orders.
We can improve the wave function systematically by multiplying by
operators PG and exp(−λK) repeatedly.
For example, we consider ψ(2) = exp(−λ'K)PG(g')ψ(1)
for different variational parameters λ' and g'.
This wave function is a very good many-body wave function because
the ground-state energy is lowered greatly and the ground-state
energy is lower than those that are evaluated by any other wave functions.
We also employ the Jastrow-type wave function which is written as
ψJ = PGPQPJψ0 where PJ indicates a nearest-neighbor number
correlation operator and PQ controls the nearest-neighbor doublon-holon correlation.
Why does the pairing state become stable?
We have shown that the superconducting phase exists in the strongly
correlated region of electronic models [3].
We investigated kinetic-energy effect in superconductivity in the
strongly correlated phase of the two-dimensional Hubbard model.
Let us examine why the superconducting state becomes stable in the
strongly correlated region.
The Gutzwiller-BCS state is stabilized as a potential energy driven
superconductivity because the Coulomb interaction energy is
lowered while the kinetic energy increases in this state.
In contrast,
we showed that in the ψλ-BCS wave function
ψλ-BCS = exp(−λK)PGψBCS, the Coulomb
energy increases and instead the kinetic energy is lowered
in the strongly correlated phase where the Coulomb repulsive interaction U is large.
The correlated superconducting state is realized as a kinetic energy driven pairing state and
this indicates the enhancement of superconductivity due to kinetic-energy effect.
We estimate the kinetic energy in the superconducting state
ψλ-BCS [6].
We define the SC condensation energy ΔEsc as a sum of
two contributions ΔEkin-sc and ΔEU-sc which originate from
the kinetic energy and the interaction energy, respectively.
We have
ΔEsc = ΔEkin-sc + ΔEU-sc.
The kinetic energy in ψλ-BCS is lower than the kinetic energy
in the normal state ψλ.
The Coulomb energy expectation value increases as Δsc increases.
The results show
ΔEkin-sc > 0, ΔEU-sc < 0,
for ψλ-BCS with U = 18t and the hole density x = 0.12.
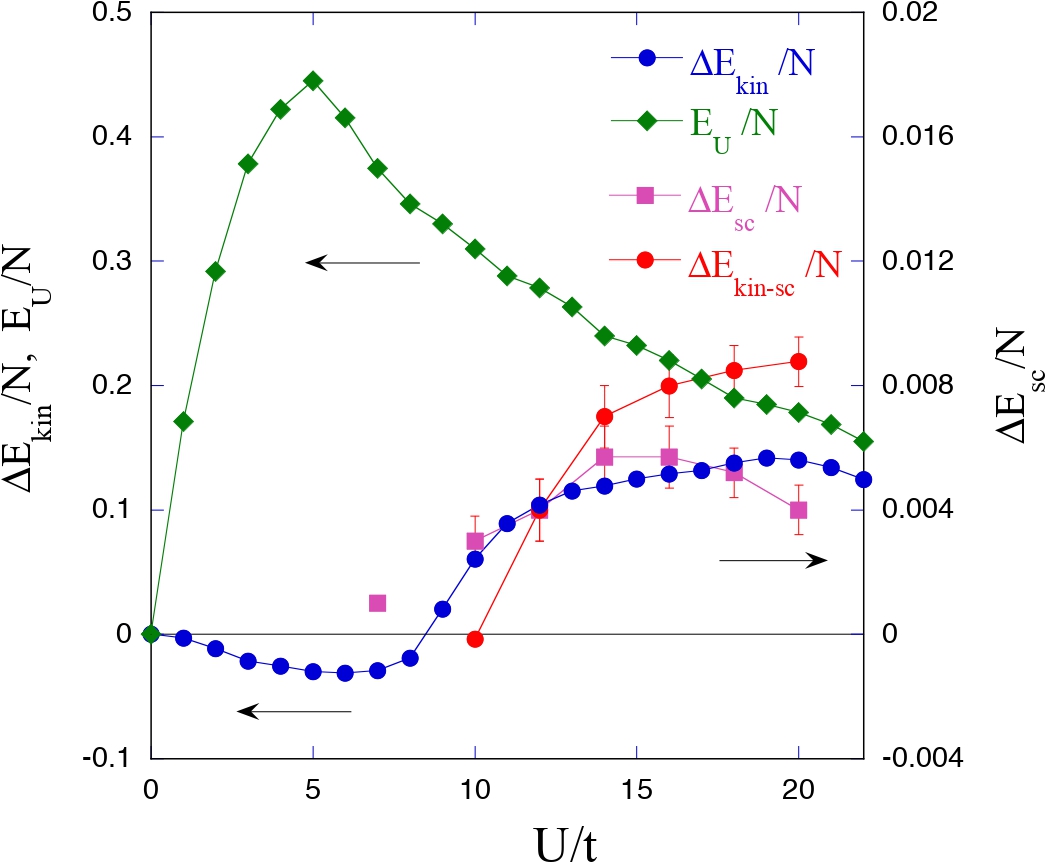
Fig. 1. Kinetic-energy difference ΔEkin/N and the kinetic-energy gain
ΔEkin-sc/N in the superconducting state ψλ-BCS
as a function of U on a 10 × 10 lattice where Ne = 88 and t'= 0.
The Coulomb energy EU/N for ψλ and the condensation
energy ΔEsc are also shown.
We use the periodic boundary condition in one direction and antiperiodic
one in the other direction.
The y axis on the right shows the superconducting condensation
energy ΔEsc and the kinetic condensation energy
ΔEkin-sc/N for ψλ.
We define the difference of the kinetic energy as
ΔEkin = Ekin(ψG) − Ekin(ψλ),
where Ekin(ψG) and Ekin(ψλ) indicate
the kinetic energy for ψG and ψλ respectively.
We can write ΔEkin = Ekin(λ = 0) − Ekin(λ)
for the optimized value of λ.
ΔEkin has the close relation with the SC condensation energy ΔEsc and its kinetic
part ΔEkin-sc.
We show ΔEkin/N in Fig. 1 for x = 0.12 where x is the hole doping rate.
The Coulomb energy EU/N and the superconducting condensation energy ΔEsc/N are also
shown in Fig. 1. ΔEkin begins to increase after the Coulomb energyEU reaches the peak
when U ≈ 8t.
The y axis on the right shows ΔEkin-sc/N in Fig. 1. ΔEkin-sc shows a similar behavior
to ΔEkin. ΔEkin-sc may change sign as a function of U, which is
consistent with the analysis for Bi2Sr2CaCu2O8 + δ [8].
This shows the kinetic-energy-driven enhancement of superconductivity.
References:
[1] T. Yanagisawa et al., J. Phys. Soc. Jpn. 67, 3867 (1998).
[2] T. Yanagisawa, Phys. Rev. B75, 224503 (2007) (arXiv: 0707.1929).
[3] T. Yanagisawa, J. Phys. Soc. Jpn. 85, 114707 (2016).
[4] T. Yanagisawa, J. Phys. Soc. Jpn. 88, 054702 (2019).
[5] T. Yanagisawa, Condensed Matter 4, 57 (2019).
[6] T. Yanagisawa, Phys. Lett. A403, 127382 (2021).
[7] T. Yanagisawa et al., EPL 134, 27004 (2021).
[8] G. Deutscher, A. F. Santander-Syro, N. Bontemps: Phys. Rev. B 72, 092504 (2005).
| |

