O(3)二次元非線型シグマモデルにインスタントン解が存在することは、Belavin-Polyakovにより最初に指摘された。
インスタントン解のまわりのゆらぎの効果は、Fateevらによって計算された（文献[2]）。この論文は非常に不思議な
難解な論文であり、いつかまとめて解説できたら面白いと思う。
There is a spin-vortex excitation in the two-dimensional ferromagnet.
This is desctibrf by an instanton solution of the nonlinear sigma model that
is obtained as a continuum limit of the ferromagnet.
The nonliner sigma model is given by the action:
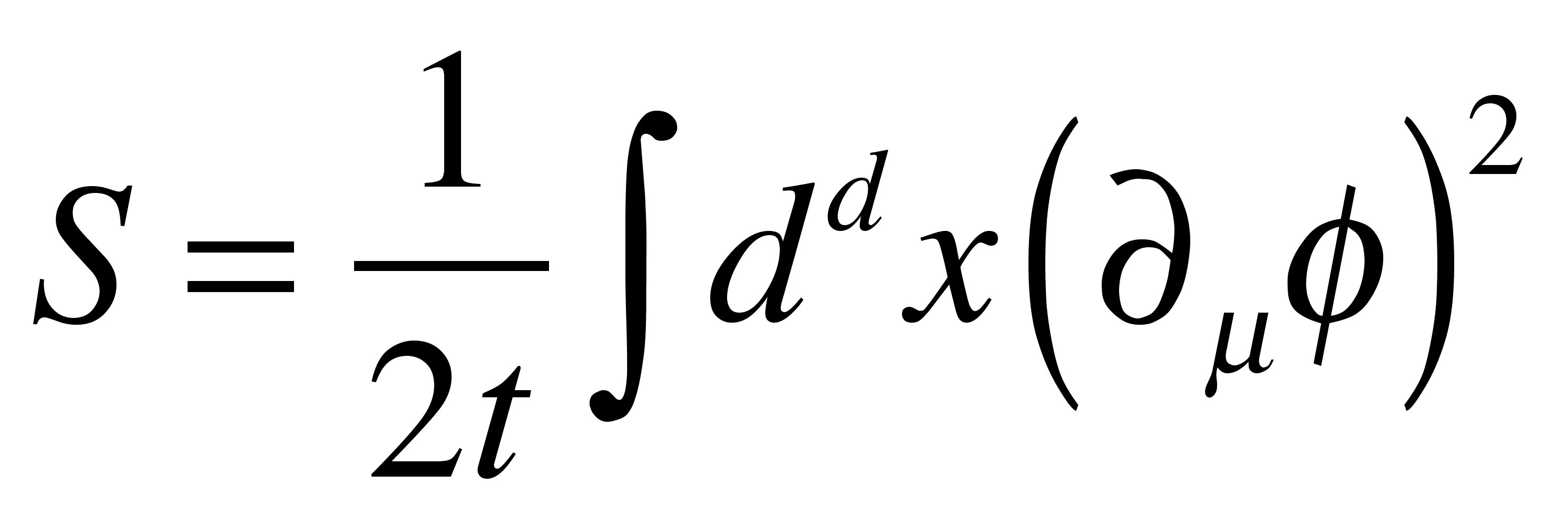
Here, &phi is an N-component scalar field satisfying &phi²=1.
It has been shown that this model has an instanton (or skyrmion) solution[1] which describes
an excitation of spin-vortex type.
It has been shown that quantum fluctuations of instantons are reduced to
the study of the Coulomb gas, and that the gas of
instantons of the 2D nonlinear sigma model is in the plasma phase [2].
The model of two-dimensional Heisenberg quantum antiferromagnet is mapped onto
the (2+1)D nonlinear sigma model.
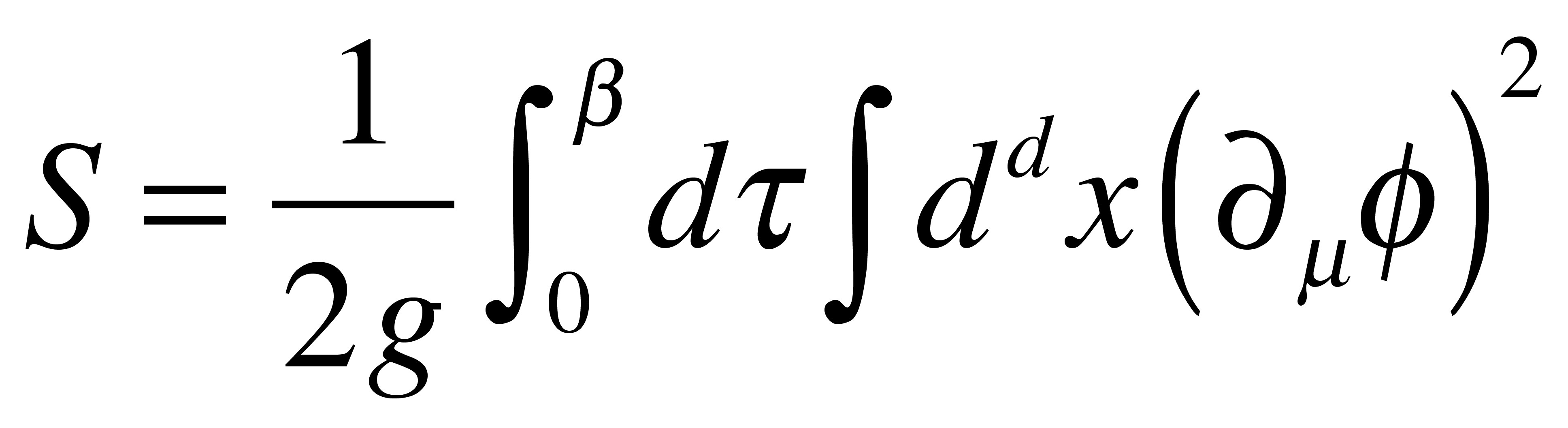
This model has also instanton solutions where we put
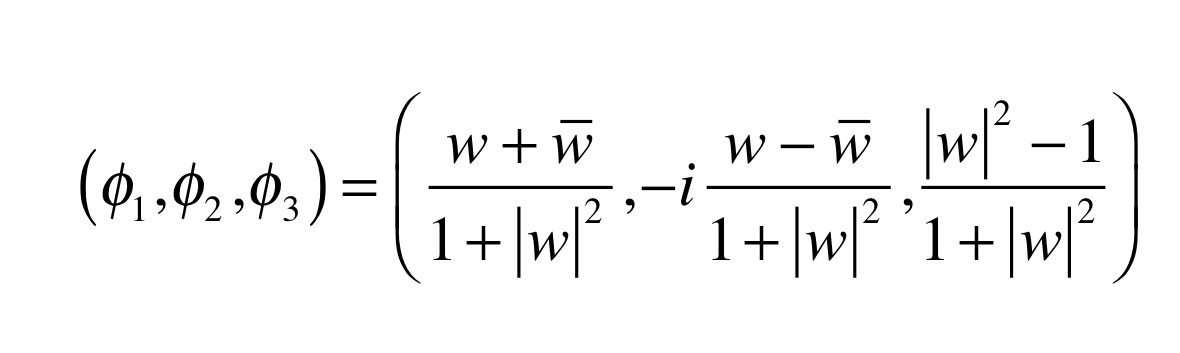The instanton solution is written as
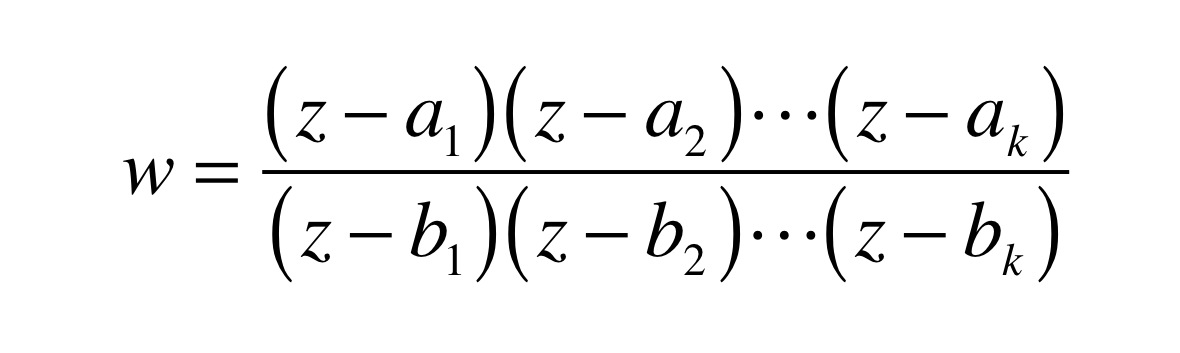We generalize the picture of instanton gas in 2D to the (2+1)D nonlinear sigma
model. We can show, using static approximation, that there is a Kosterlitz-Thouless
transition from
the plasma phase to the molecular phase as the temperature is lowered [3].
References:
[1] A.A. Belavin and A.M. Polyakov: JETP Lett. 22, 245 (1975).
[2] V.A. Fateev, I.V. Frolov, A.S. Schwarz: Nuclear Physics B154, 1 (1979).
[3] T. Yanagisawa: J. Phys. Conf. Series 428, 012040 (2013).
| |
