|
|
| |

Non-abelian sine-Gordon model
| |
|
|
|
| |
The sine-Gordon model has a universality and appears in various fields of physics [1-4].
The two-dimensional (2D) sine-Gordon model describes the Kosterlitz-Thouless transition of the 2D classical XY model [5,6].
The 2D sine-Gordon model is mapped to the Coulomb gas model with logarithmic interaction [7].
The Kondo problem also belongs to the same universality class where the scaling equations are given by those for the 2D sine-Gordon model [8].
The one-dimensional Hubbard model is also mapped onto the 2D sine-Gordon model by using a bosonization method [9,10].
The sine-Gordon model plays an important role in superconductors, especially multi-band superconductors including layered high-temperature superconductors [11,12].
Generalized sine-Gordon models have also been investigated.
The chiral model was generalized to the Wess-Zumino-Witten (WZW) model by including the Wess-Zumino term [13-15].
The WZW model gives a model of conformal field theory whose current algebra is realized by a Kac-Moody algebra.
The massive chiral model, which is the chiral Lagrangian [16,17] or the non-linear sigma model with the mass term, is also interesting as a
two-dimensional field theory.
The massive chiral model can be regarded as a generalization of the sine-Gordon model to the model for G-valued fields,
where we add the term of type Tr(g+g-1) for g ∈ G where G is a general gauge group (Lie group).
We believe that a family of non-abelian sine-Gordon models will describe the physics of the universe.
We investigated the chiral sine-Gordon model using the renormalization group method.
The chiral sine-Gordon model is a model for G-valued fields and describes a new class of phase transitions, where G is a compact Lie group.
We show that the model is renormalizable by means of a perturbation expansion and we derive beta functions of the renormalization group theory.
The coefficients of beta functions are represented by the Casimir invariants.
The model contains both asymptotically free and ultraviolet strong coupling regions.
The beta functions have a zero which is a bifurcation point that divides the parameter space into two regions; they are the weak coupling region and the strong coupling region.
A large-N model is also considered. This model is reduced to the conventional sine-Gordon model that describes the Kosterlitz-Thouless transition near the fixed point.
In the strong-coupling limit, the model is reduced to a U(N) matrix model.
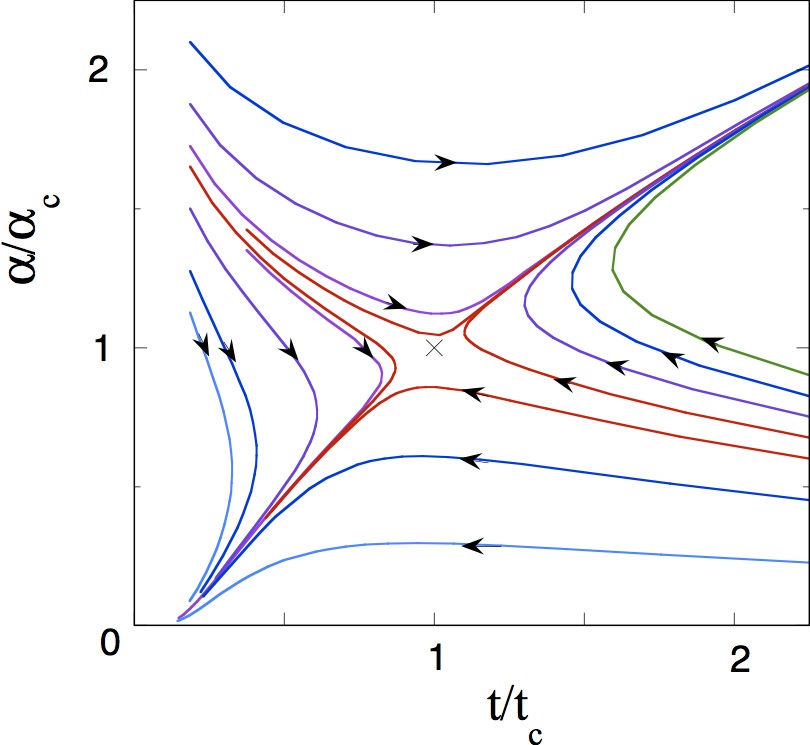
Fig. Renormalization group flow for the SU(N) sine-Gordon model [18].
References:
[1] R. F. Dashen et al., Phys. Rev. D11, 3424 (1975).
[2] A. B. Zamolodchikov and Al. B. Zamolodchikov, Ann. Phys. 120, 253 (1975).
[3] R. Rajaraman, Soliton and Instanton (North-Holland, Amsterdam, Netherlands, 1982).
[4] N. S. Manton and P. Sutcliffe, Topological Solitons (Cambridge University Press, Cambridge, 2004).
[5] J. M. Kosterlitz and D. Thouless, J. Phys. C6, 1181 (1973).
[6] J. M. Kosterlitz, J. Phys. C7, 1046 (1974).
[7] J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford Unviersity Press, Oxford, 1989).
[8] J. Kondo, The Physics of Dilute Magnetic Alloys (Cambridge University Press, Cambridge, 2012).
[9] J. Solyom, Adv. Phys. 28, 201 (1979).
[10] F. D. N. Haldane, J. Phys. C14, 2585 (1981).
[11] A. J. Leggett, Prog.Theor. Phys. 36, 901 (1966).
[12] T. Yanagisawa et al., J. Phys. Soc. Jpn. 81, 024712 (2012).
[13] J. Wess and B. Zumino, Phys. Lett. B37, 95 (1971).
[14] E. Witten, Nucl. Phys. B223, 422 (1983).
[15] E. Witten, Commun. Math. Phys. 92, 455 (1984).
[16] V. L. Golo and A. M. Perelomov, Phys. Lett. B79, 112 (1978).
[17] E. Brezin, C. Itzykson, J. Zinn-Justin and J. B. Zuber, Phys. Lett. B82, 442 (1979).
[18] T. Yanagisawa, EPL 113, 41001 (2016).PDF
| |
|
| |
| |

