多体電子論の基礎であるフェルミ流体論について議論したいと思います。
フェルミ流体論はランダウによって最初に考えられましたが、凡人の理論ではないためその奥は深いものに
なっています。ランダウの手のひらはお釈迦様の手のひらのように広く、
その上で踊るのは簡単ですが、その前にその理論を吟味してみることは必要でしょう。
ランダウーリフリッツの物理学教程の教科書を読みますと、計算量がものすごいために、ランダウもそのように計算をしながら
研究を進めていたのだと思いがちですが、ランダウの物理の特徴はいかに計算をせずに物理を引き出すかにあるように感じます。
ランダウの二次相転移の理論を見てもそうですが、非常に簡単なモデルから多くの物理が出てきます。
フェルミ液体論もまさにそのような理論であり、簡単な仮定から出発して電子系の基礎となる理論が展開されます。
１.フェルミ縮退した電子系
２.ランダウのフェルミ流体論
３.ハバードモデルの摂動論
４.近藤効果ー典型的なフェルミ流体ー
５.ラッテインジャーのフェルミ流体論
1. フェルミ縮退した電子系
電子間にはクーロン相互作用が働くにもかかわらず、自由電子の近似による計算がうまくいくことが、非常にしばしばおこります。
これはバンド計算が成功することが多いことからもわかります。この理由は何でしょうか。
これは電子がフェルミオンであることによっています。
エネルギーが低いレベルから順番に電子が詰まっていくためフェルミ面が存在することになります。
相互作用により散乱される電子はフェルミ面近くの電子に限られるために、電子の散乱確率が非常に弱められます。
フェルミ面近くの電子はeV（電子ボルト、温度に直すとおよそ一万度）という非常に大きなエネルギーをもっています。
温度が少しくらい変化しても電子系のエネルギーはあまり変わらないことになります。
そのため、電子系の比熱は気体分子運動論により予想されるものより非常に小さくなります。
金属中の電子のエネルギーは
フェルミエネルギー εF ∼ eV
相互作用エネルギー e2/r ∼ eV
のように非常に大きい。それにもかかわらずフェルミ縮退した電子系では低温において
自由電子系の描像が成り立つ
ことがあります。その理由を考えてみましょう。
そのために、電子ー電子散乱による電子の寿命を見積もってみます。
フェルミ面近くの電子が散乱され、散乱される電子はフェルミ面からエネルギーがkBTの範囲にいるものが、
主として散乱されますので、電子の散乱確率W=1/τは低温では温度Tの2乗に比例することになります。すなわち、
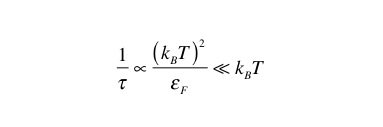低温では温度kBTに比べて小さく、小さな補正とみなすことができます。
このため、低温では電子はあたかも自由電子のように振舞うと考えてよいことになります。
このことがランダウのフェルミ流体論の基礎となっています。
ここで、どうして散乱確率が温度の2乗に比例するかを考えてみましょう。
簡単にいいますと、エネルギー保存則と運動量保存則とフェルミ統計による制限のために、散乱が抑えられているからです。
自己エネルギーに相当する散乱の図を下に示します。
点線は相互作用を表わし、実線は相互作用している電子を意味しており、この図は2次の摂動による散乱を表わしています。
散乱確率はこの図の虚数部で与えられますが、これのエネルギー依存性をみてみましょう。
この虚数部は三本の実線に対応するグリーン関数の虚数部の積となりますので（いわゆる光学定理とよばれるものです）、
三つのデルタ関数の積となります。デルタ関数はエネルギーの保存を表わしますので、
それらの制限からこの図の虚数部はエネルギーが小さい時はその2乗に比例することになります。
温度に直しますと、温度の2乗に比例することになるわけです。
（なお、ここでは空間の次元は3次元としています。）
このことを確かめるために具体的なモデルに対して計算してみましょう。
（つづく）
| |
