自然界において、磁束は任意の実数値を取り得ますが、超伝導体中においては状況が異なります。第二種超伝導体においては、
磁場が渦糸状に超伝導体の中に入り込みますが、この渦糸の磁束は単位量子磁束の整数倍に量子化されます。すなわち、
磁束の量子化が起こります。これは、ギャップ関数(電子対の波動関数)が一価であるという要請からきます。
渦糸の周りを電子対が一周した時に、電子対の波動関数が元に戻るということです。
一価性の条件は幾何学的なものです。すなわち、磁束の量子化はトポロジカルな現象です。
超伝導体の幾何学的形状によっては、整数量子化が破れる場合もあり得ます。
複数の量子位相が存在する系においては、量子化条件も一般化されたものとなります。
例えば、層状超伝導体においては、各層ごとに量子位相が存在し、整数量子化が破れ単位磁束の非整数倍の磁束が存在し得ます。
複数の量子位相が存在する系においては、新しいトポロジカル現象が存在することになります。
数学的には指数定理に関係しています。Atiyah-Singerの指数定理においては指数は整数ですが、境界がある多様体に対しては、
境界からの寄与があります(Atiyah-Patodi-Singerの指数定理)。
境界からの寄与は一般に整数ではなく、境界のある多様体上の積分も一般には非整数になります。
同様のことが量子系においても起こり、非整数量子化が起こり得ることになります。
整数量子化から非整数量子化へと現象が一般化されます。
二成分超伝導体における非整数量子磁束については以下のように説明できます。
There are solutions of vortices with fractionally quantized flux in multiband superconductors.
The existence of fractionally quantized-flux vortices is very interesting and attractive.
The phases of gap functions are important and the kink (soliton) solution of phase difference plays a central role
for the existence of fractional flux vortices.
In a two-band model, the half-quantum-flux vortex exists at the edge of a line singularity of the phase
variables (see Fig.1 where θ denotes the phase of the gap Δ1). θ changes from 0
to π across the singularity, while the phase θ2 of the gap Δ2 changes
from 0 to -π. In two regions above and below the singularity line, the phase difference
θ1-θ2 is 0 mod 2π. Thus the energy costs due to Josephson couplings are
the same there. In the case of Fig.1, a net-change of θ1 is 2π by a counterclockwise
encirclement of the vortex, and that of θ2 vanishes. This results in a half-quantum flux vortex.
The existence of a half-flux vortex in triplet superconductors have also been predicted [3].
A generalization to a three-gap superconductor is not trivial.
We have very attractive features, that is, chiral states with time-reversal
symmetry breaking and the existence of fractionally quantized vortices.
Further, in the case with more than four gaps, a new state is predicted with a gapless excitation mode.
There are many types of kinks connecting two minima of the potential in three-band superconductors.
In a three-band model, a fractional vortex has two line-singularities (kinks) in the phase of the gap functions.
Two vortices can form a molecule by two kinks. Three-vortex bound states are also formulated, corresponding
to baryons when we regard the magnetic flux as charge.[1]
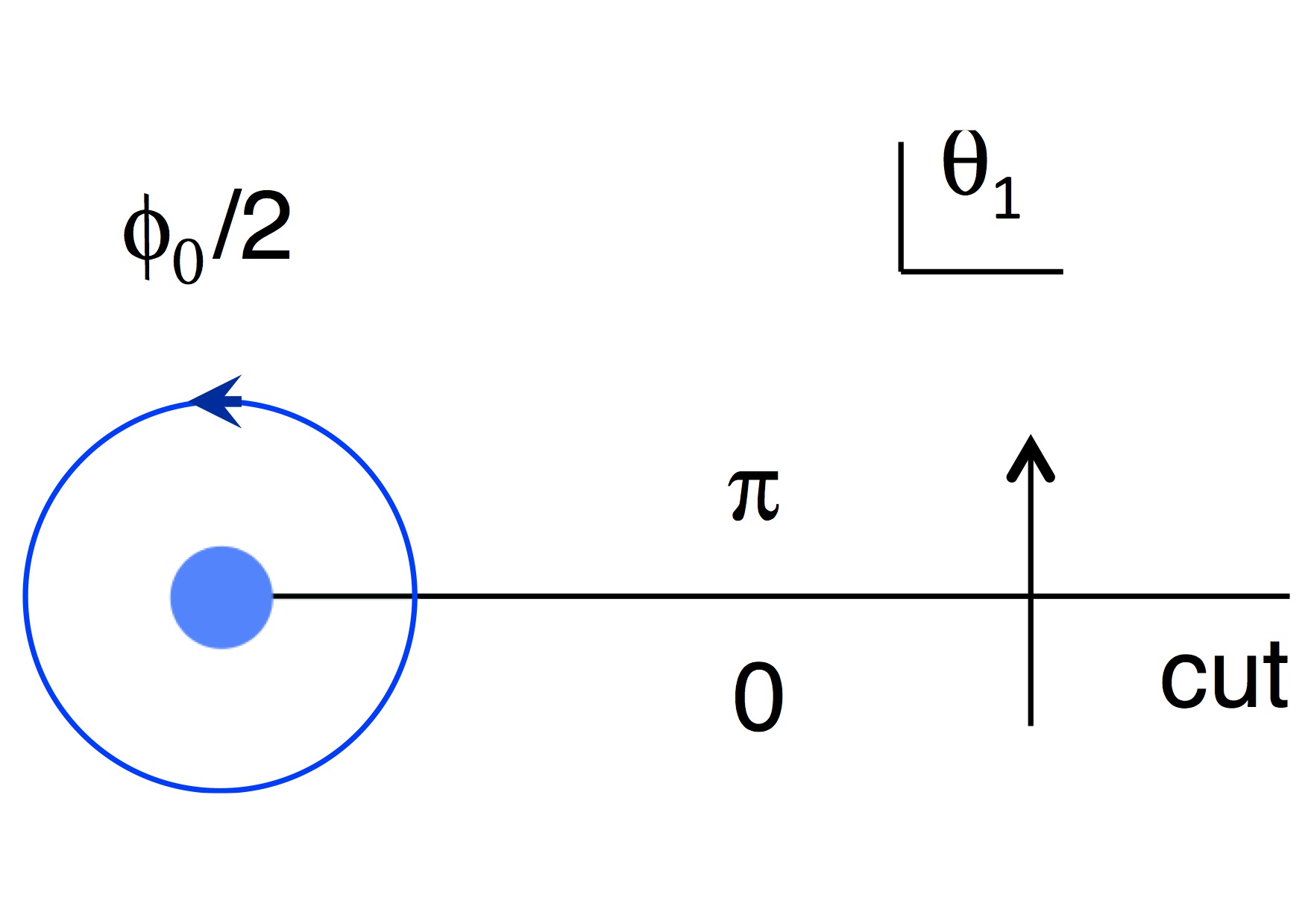
Fig.1. Half-flux vortex and a singularity of the phase variable θ1.
References:
[1] T. Yanagisawa et al.: J. Phys. Soc. Jpn. 81, 024712 (2012).
[2] Yu. A. Izyumov and V. M. Laptev: Phase Transitions 20, 95 (1995).
[3] G. E. Volovik: J. Exp. Theor. Phys. Lett. 70, 792 (1999).
| |

