非線型シグマモデルは不思議なモデルであり、物理学のあらゆるところに顔を出します。何らかのユニバーサリティーを持ったモデルのようです。
スピン系のモデルである古典的ハイゼンベルグモデルは連続極限を取ると、非線型シグマモデルとなります:
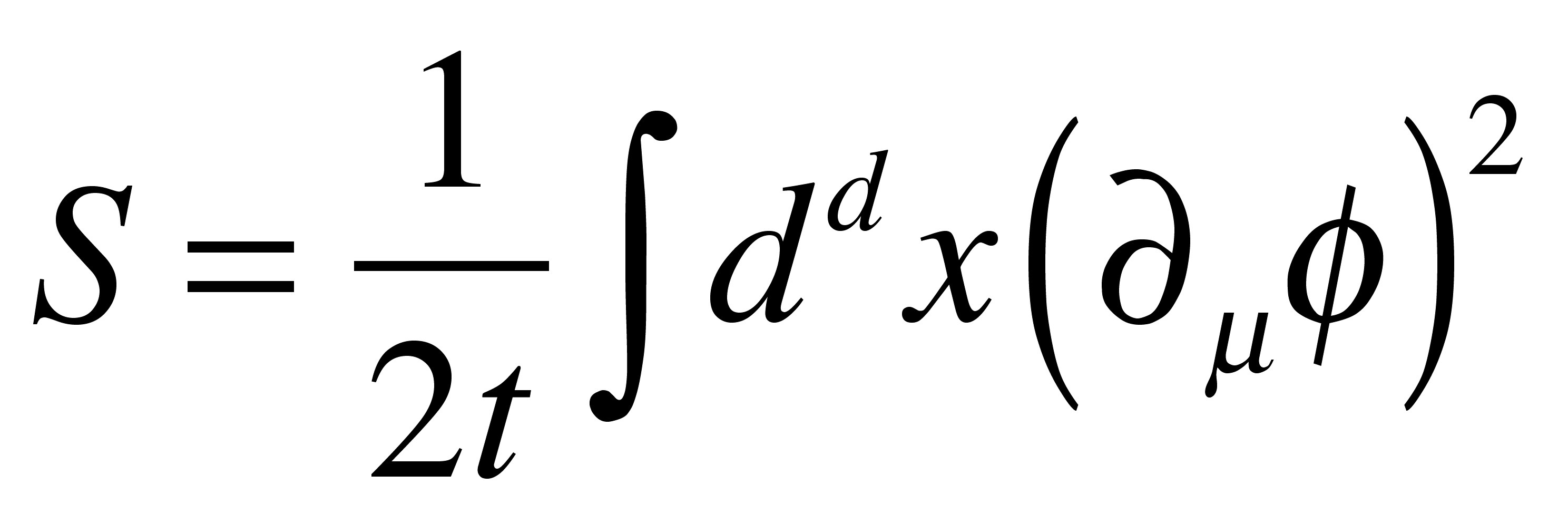
ここで、&phiは&phi²=1を満たすN成分スカラー場であり、tは温度を表すパラメーターです。
空間2次元では、この0(3)非線型シグマモデルは漸近自由性を示し、4次元の非可換ゲージ理論との類似性があります。また、近藤効果との類似性もあります。0(3)シグマモデルにインスタントン解が存在することも ([1] [2] [3])、非可換ゲージ理論との類似点です ([4][5])。
古典ハイゼンベルグモデルから得られた非線型シグマモデルはスピン波を記述していると考えられます。d次元の量子系は(d+1)次元の古典系に等価であることから、d次元量子ハイゼンベルグモデルは、連続極限では(d+1)次元の非線型シグマモデルとなります。実際、二次元量子ハイゼンベルグモデルの相関関数< Si&sdot Sj> をスピン波近似で計算すると、(2+1)次元のシグマモデルに対して計算した相関関数と同じものになります。(このような計算を以前、文献[6]にて行いました。)空間二次元では、長距離秩序は絶対零度 T= 0のみに存在し、高温では二次元古典系に近づきますので、漸近自由性が復活するというモデルになっています ([6])。高温(高エネルギー)で漸近自由であり、T= 0に固定点が存在するのは、近藤効果との類似性があり、クォーク閉じこめとの類似性もあります。(d+1)次元の非線型シグマモデルは次で作用で与えられます。
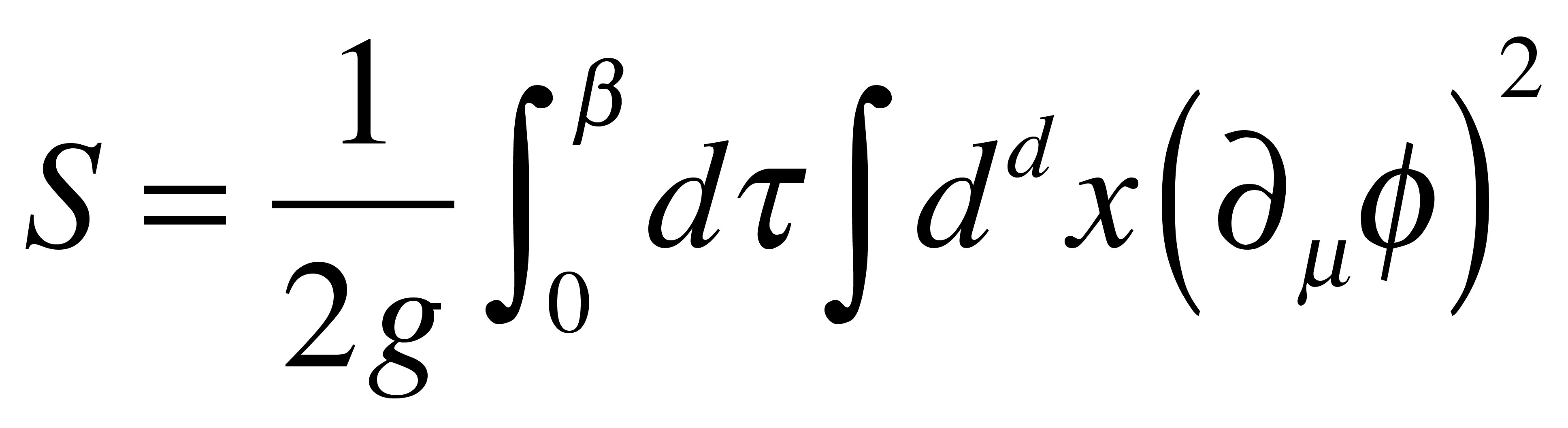
2次元非線形シグマモデルの相関長は低温で指数関数的に増大することが知られています:&xi &sim C (T/2&pi ) exp(2&pi /T) ([7][8])。
(2+1)次元のモデルの相関長も温度について指数関数的になります ([6][9]):
&xi &sim C&xiexp(2&pi JF/T)。
量子効果があっても低温で指数関数的に増大するというのは同じになります。指数関数の1/Tの係数Fはモンテカルロ法を使った数値計算によると、およそF = 0.22とされており、くりこみ群の3ループまでの計算によると
F = 0.26
であり、ほぼ一致する値が得られています ([6])。(2+1)次元系ではFに対して量子効果による補正が生じることになります。
参考文献
[1] A.A. Belavin and A.M. Polyakov: JETP Lett. 22, 245 (1975).
[2] V.A. Fateev, I.V. Frolov, A.S. Schwarz: Nuclear Physics B154, 1 (1979).
[3] B. Berg and M. Lü scher: Comm. Math. Phys. 69, 57 (1979).
[4] A.A. Belavin, A.M. Polyakov, A.S. Achwarz, Y.S. Tyuokin: Phys. Lett. B59, 85 (1975).
[5] G. 'tHooft: Phys. Rev. D14, 3432 (1976).
[6] T. Yanagisawa: Renormalization of the quantum antiferromagnet in two dimensions: Phys. Rev. B46, 13896 (1992).
[7] S.H. Shenker and J. Tobochnik: Phys. Rev. B22, 4462 (1980).
[8] Y. Iwasaki: Prog. Theor. Phys. 68, 448 (1982).
[9] S. Chakravarty, B.I. Halperin, D.R. Nelson: Phys. Rev. B39, 2344 (1989).
| |

