銅酸化物高温超伝導体においては、チェッカーボードやストライプなどとよばれるちょっと変わった状態が、実験により報告されています。
ストライプというのはホールが一列に並んだ状態です。このような状態が実際に可能かどうかをハバードモデルに対する変分モンテカルロ
計算によって調べました。ホールが並ぶと言っても本当にそこにホールがとどまっているというわけではなく、ホール密度が直線状に
高くなっているということです。電荷密度の空間変化は図1のようになります。
反強磁性状態とストライプが共存すると、Q=(&pi,&pi)の反強磁性より安定になることがあります。
ストライプ的になりますと、反強磁性相関のピークがQ=(&pi,&pi)からずれますが、そのずれを非整合度（incommensurability)というと、
非整合度はほぼホール濃度に比例することが示されます。（図2）[1][2]
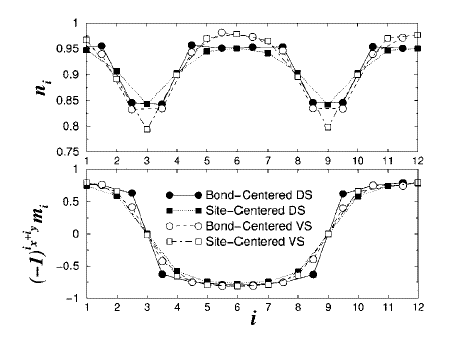図1. ストライプに垂直な方向への電荷とスピンの空間依存性。[1,2]
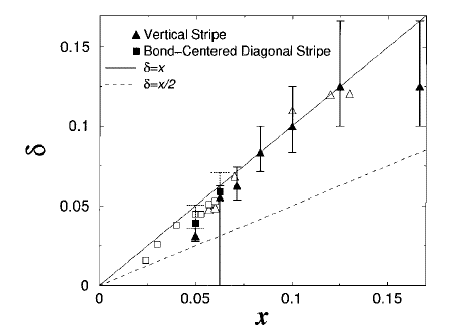図2. 非整合度のホール濃度依存性。[1]
チェッカーボード状態というのは、電子密度がチェッカーボード的になっている状態です。例えば、スピン構造は下図のようになっています。
スピンの配置がちょうどチェッカーボードのような形をしています。
このような状態では明らかに電子、またはホールの運動エネルギーを損しますので、なかなか安定になりにくい状態です。
バンドパラメーターに関して狭い領域においてですが、チェッカーボード的状態が安定になることがわかりました。[3]
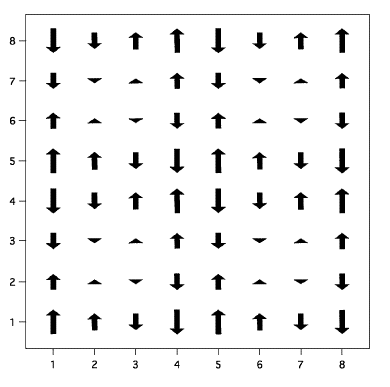図3. チェッカーボード状態におけるスピン構造。[3]
文献
[1] Diagonal Stripe States in the Light-Doping Region in the Two-Dimensional Hubbard Model
M. Miyazaki, T. Yanagisawa, K. Yamaji: Journal of the Physical Society of Japan 73 (2004) 1643.
[2] Stripe formation in high-Tc superconductors
T. Yanagisawa, S. Koike, M. Miyazaki, K. Yamaji: Journal of Phyisics: Condensed Matter 14 (2002) 21.
[3] Checkerboard States in the Two-Dimensional Hubbard Model with the Bi2212-Type Hubbard Model
M. Miyazaki, K. Yamaji, T, Yanagisawa, R. Kadono: Journal of the Physical Society of Japan 78 (2009) 043706.
| |
