量子モンテカルロ法においてフェルミ粒子系に対する波動関数は次で与えられる。
 ,
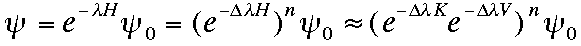ここで, λ = nΔλ である。この波動関数により物理量の期待値を計算しようとすると、負符号問題が起こることがある。
行列式が負になることがあり, 期待値が
〈 Q 〉 ≈ (Q+− Q−)/(M+− M−)
のように表わされ, もしも M+≈ M−であると, 分母がゼロになり期待値が計算できなくなる。
これが負符号問題である。
このような系をどのように取り扱うかを考えよう。
最適化された波動関数による量子変分モンテカルロ法においては, 波動関数をより一般化して次の波動関数を考える。
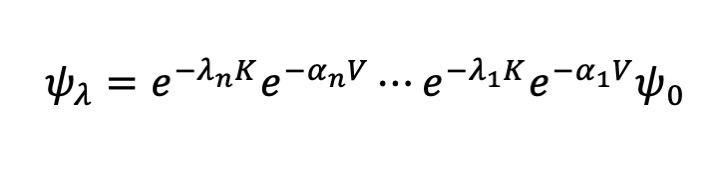ここで, λj と αj (j = 1, …, n) は変分パラメーターである。
この波動関数は ψ の一般化と考えてよく, ψ は ψλ において λj と
αj をすべて同じにした場合である。
λj と αj をパラメーターとしてエネルギー期待値を下げるように決めると,
負符号が抑えられることがわかる。図1に二次元ハバードモデルに対する計算結果を示す。
縦軸はエネルギーEであり, 横軸は符号sの期待値 〈 s 〉 を表わす。負符号問題は 〈 s 〉 → 0
の時に深刻となり, 物理量の期待値が計算できなくなる。図1からわかるように, λj と αj
により変分することによりエネルギー期待値が下がり,
符号 〈 s 〉 は有限の値となり (≠ 0) 負符号は問題ではなくなる。
図1の点Eは負符号問題の場合であり期待値を計算することはできない。ここでは、変分した場合 (A, B, C, D)から外挿した値を示した。
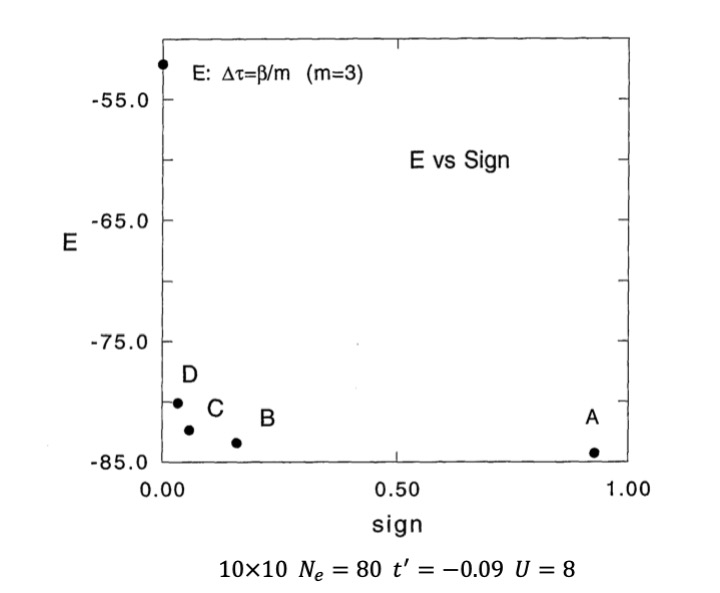
Fig.1. 基底状態のエネルギーと符号 ([2]).
このように波動関数をマルチパラメーターの空間で考えることにより, 負符号問題を回避することができる。
パラメーターの空間の次元を大きくする, すなわち波動関数の空間を広げてその中で考えようということである。
（これを, 「上空移行の原理」とよぼう。）
また, 計算に変分プロセスが入ることにより一般に計算量が増える。
参考文献
[1] Off-diagonal wave function Monte Carlo studies of Hubbard model I
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 67, 3867 (1998).
[2] d-wave state with multiplicative correlation factors for the Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 68, 3608 (1999).
[3] Off-diagonal wave function Monte Carlo studies of Hubbard model II
T. Yannagisawa: Journal of the Physical Society of Japan 85, 114707 (2016).
[4] Off-diagonal wave function Monte Carlo studies of Hubbard model III
T. Yanagisawa: Journal of the Physical Society of Japan 88, 054702 (2019).
| |
