強い電子相関に伴うスピン及び電荷揺らぎにより高温超伝導が引き起こされます。
高温超伝導体のように電子相関の強い系の電子状態を明らかにするためには、電子間相関を適切に考慮した波動関数を考える必要があります。
我々の研究において、強相関電子系に対する多体の波動関数を改良して最適化し、世界的に見て最良の波動関数を得ました。これまで世界中の研究者により色々な多体波動関数が考察されてきましたが、我々の波動関数はそれらのどの波動関数よりもエネルギー期待値が下がり、最良の波動関数であることを示すことができました。最適化された波動関数による期待値の計算は、モンテカルロ法を使うことにより、波動関数の正しい期待値が得ることができます。この波動関数に基づいて、二次元ハバードモデル及びd-pモデルの基底状態の電子状態を調べました。キャリアーがドープされた系において、電子間相互作用が強くなるに従い、弱相関領域から強相関領域へのクロスオーバーが起こることを示しました。すなわち、オンサイトクーロン相互作用Uの関数として見ると、反強磁性相関はUがほぼバンド幅の大きさに等しい時に最大を示し、さらにUが大きくなると減少に転じます。クーロン相互作用Uが大きい領域で反強磁性相関が抑えられるのは、反強磁性によるエネルギーの下がりが1/U
のように小さくなるからです。よりエネルギーを下げるために、反強磁性の相関を壊してホールを動かし、運動エネルギーを得しようとするわけです。強相関領域において反強磁性相関が抑えられることにより、強いスピン揺らぎが生じます。この強いスピンゆらぎ、及び増大した運動エネルギーが高温超伝導を引き起こします。我々の計算により、このような描像が得られました。実際、超伝導相関はこの領域において増大することを示しました。これより、高温超伝導は弱相関から強相関へのクロスオーバーに伴って起こると言うことができます。クロスオーバーに伴う特異性が超伝導の起源です。このクロスオーバーにともなう特異性の出現は非常に普遍的な現象であると考えられます。例えば、有名な近藤効果における対数特異性も、弱結合状態から強結合状態へのクロスオーバーにおいて生じるものです。すなわち、強相関ゆらぎによる高温超伝導と近藤効果とは、同じユニバーサリティークラスに属していると言えます。
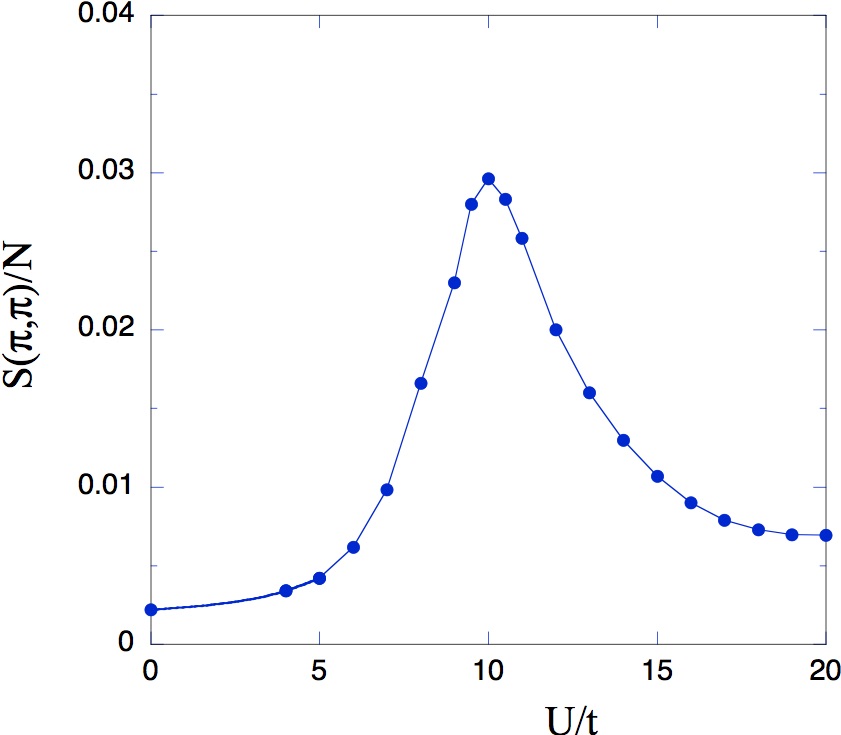
図1. 反強磁性相関とクーロン相互作用 ([1])。
U/tが非常に大きくなると、反強磁性相関は減少に転ずる。
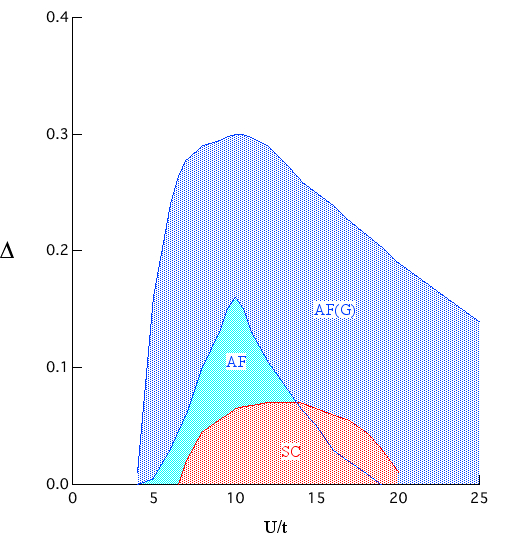
図2. 秩序パラメーターとクーロン相互作用の強さ([1])。
最適化モンテカルロ法による相図。クーロン相互作用が大きい強相関領域において高温超伝導が可能となる。
文献
[1] Crossover from weakly to strongly correlated regions in the two-dimensional
Hubbard model -- Off-diagonal Monte Carlo studies of Hubbard model II --
T. Yanagisawa: Journal of the Physical Society of Japan 85, 114707 (2016).
[2] Off-diagonal wave function Monte Carlo studies of Hubbard model I
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 67, 3867 (1998).
[3] Mott transition in cuprate high-temperature superconductors
T. Yanagisawa, M. Miyazaki: Europhysics Letters 107, 27004 (2014).
[4] Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model
T. Yanagisawa, M. Miyazaki, K. Yamaji: Journal of the Physical Society of Japan 78 (2009) 013706.
[5] Gorund state of the three-band Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Physical Review B64, 184509 (2001).
参照記事
つくばサイエンスニュース『高温超電導現象の発生機構解明で新理論』
| |

