2次元d-pモデルに対して波動関数によるエネルギーの期待値を変分モンテカルロ法により計算して安定な状態を調べました。6× 6と8× 8の系において、反強磁性と超伝導状態を基底状態の候補として、秩序状態になったことによるエネルギーの下がりをキャリアーのドープ量の関数として書くと下の図のようになります（図1）([1])。特徴として、ホール濃度が低い領域に反強磁性相があり、その外にd波の超伝導相があることがあげられます。ホール濃度が負の領域は電子ドープであることを示しています。ホールドープと電子ドープとで、相図に非対称性があります。ここでは、酸素のp軌道間の重なり積分tppを0にしていますが、tppを有限にして大きくしていくと、非対称性も小さくなる傾向があります。
また、ドーピング量が小さい時は、s波（異方的）の超伝導状態の方がd波よりも安定な領域があります。ここでは、反強磁性の方がこの二つよりも安定ですが、反強磁性が何らかの理由で安定でなくなると、s波の可能性もあります。これは3バンドモデルに特有のことであり、1バンドのハバードモデルやt-Jモデルにはない相です。
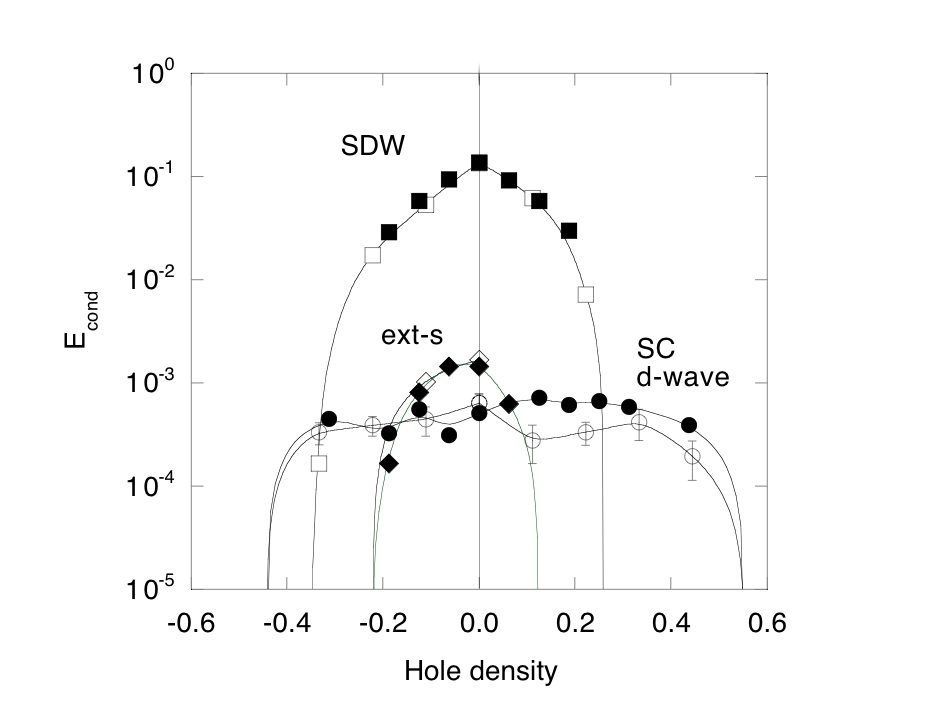図1. 6× 6、8× 8における変分モンテカルロ法による相図。
（白抜き記号が8× 8の系に対する結果。）
反強磁性と超伝導は共存する可能性が、共存状態まで含めてエネルギーを計算し、書いた相図が下の図です。系のサイズを16× 16、
32× 8まで
計算し、サイズについての外挿を行いました。低ドープ域では反強磁性とd波超伝導が共存し、ドープ量を増やすと純粋なd波の状態になります。
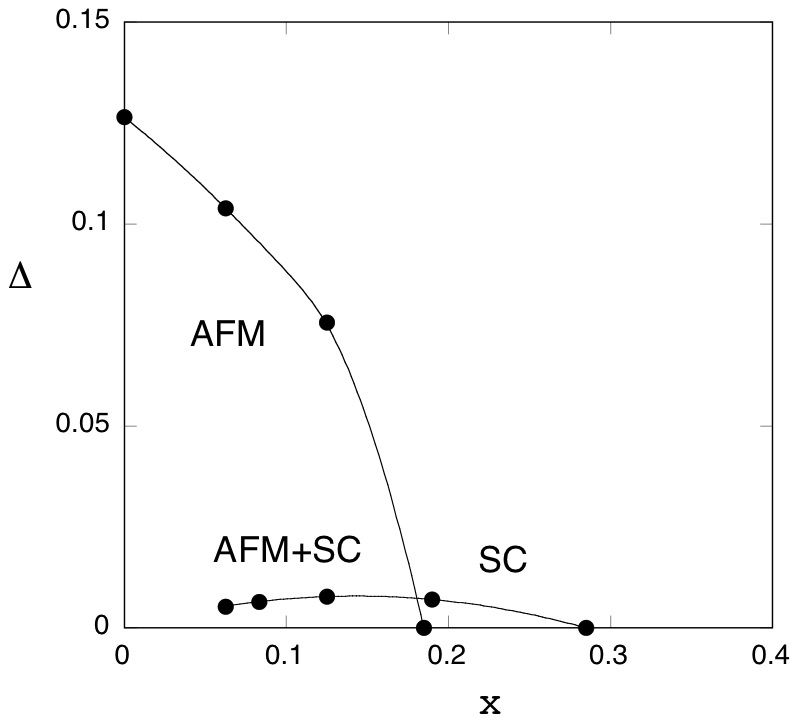
図2. 反強磁性と超伝導の共存も考えたd-pモデルの相図。[2]
文献
[1] Gorund state of the three-band Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Physical Review B64, 184509 (2001).
[2] Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model
T. Yanagisawa, M. Miyazaki, K. Yamaji: Journal of the Physical Society of Japan 78 (2009) 013706.
[3] A. Tsukada, Y. Krochenberger, M. Noda, H. Yamamoto, D. Manske, L. Alff, M. Naito: Solic State Commun. 133 (2005) 427.
| |
