変分モンテカルロ法は電子間の相関を数値的に正しく考慮することにより、波動関数の期待値を計算する方法です。いくつかの長距離秩序をもった波動関数を仮定するため波動関数は厳密ではありませんが、負符号が現われることはありません。相関のの弱い領域から強い領域まで計算を行うことができることが特徴です。
変分モンテカルロ法は下の式で表わされるエネルギー最小原理に基づいています。
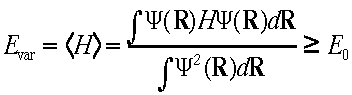
強相関電子系における標準的な波動関数は電子相関の因子を一体の波動関数にかけることにより得られます。これはGutzwillerの波動関数と言われています。
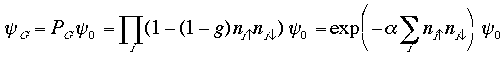
基底状態のエネルギーの計算例
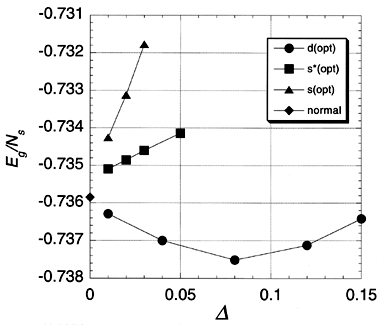
これはBCS-Gutzwiller関数に対して超伝導オーダーパラメーターを変えて10x10の格子上で基底状態のエネルギーを計算したものです。(U=8としています。)d波対称の波動関数に対してエネルギーの極小が存在することがわかります。これはd波超伝導の可能性を示しています。このような結果が得られたことは我々にとっても驚きでありました。
Ref. T. Nakanishi et al.: J. Phys. Soc. Jpn. 66 (1997) 294-297.
K. Yamaji et al: Physica C304 (1998) 225-238.
基底状態の厳密な波動関数は次の式で表わされます。
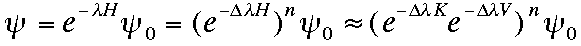
この式は、指数関数の因子をくり返し掛けることにより波動関数を改良できることを示しています。改良された波動関数により得られた基底状態のエネルギーのグラフを下に示します。(half filled 二次元ハバードモデル。)丸印は量子モンテカルロ法により得られた結果(Hirschによる)を示しており、よく合っています。
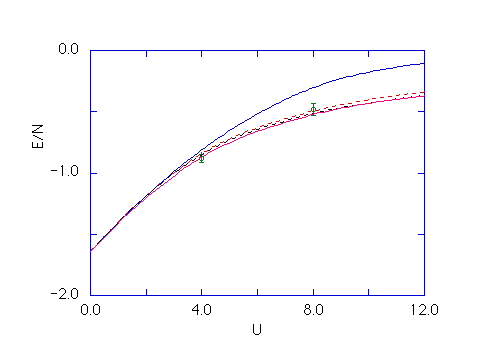
Ref. T. Yanagisawa et al.: J. Phys. Soc. Jpn. 67 (1998) 3867.
| |

