量子モンテカルロ法は、多体粒子系において物理量の期待値を正しく計算しようとする方法です。
多体電子系においては、ハバードモデルなどに応用されています。ハミルトニアンを H とすると、
基底状態の波動関数は
ψ = e−λ H ψ0,
と書くことができます。ψ0は初期波動関数でフェルミ球などの一電子状態をとります。
λ が十分に大きいと、指数関数の因子が ψ0 から基底状態を取り出すわけです。
この波動関数は取り扱いにくいので、ハミルトニアンを
H = K+V
のように非摂動項 K と相互作用項 V に分けて、次の形に書きます。
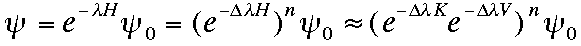
ここで、λ = nΔ λ です。n が大きいとこの近似は成り立つと考えられます。
相互作用項 V はフェルミ粒子の演算子について高次ですので、
ハバード・ストラトノビッチ変換により二次形式にします。
ハバード・ストラトノビッチ変数についての非常に大きな自由度について和をとる必要が生じます。
この形にして物理量を計算する一つの方法が量子モンテカルロ法です。
単純に計算しようとすると、負符号問題が生じて計算できなくなることがあります。
負符号を避けて計算する一つの方法が、我々が提案した最適化量子変分モンテカルロ法です。([1− 4])
ここでは、別の試みを紹介します。ハバード・ストラトノビッチ変換により波動関数は次のように書けます。
ψ = ∑mcmφm.
φm はハバード・ストラトノビッチ変数により表される状態であり、形式的にそれらの一次結合として書けます。
そこで、
{ φm } を波動関数の基底と考えて対角化により係数 cmを決めるという方法があります。
このような手法を[5]において行いました。厳密対角化を行いますので、負符号問題というものはありません。
計算に取り入れる状態数を Nstates としますと、もし物理量の期待値が Nstates
にあまり依らないなら Nstates→ ∞ への外挿により正しい期待値を求めることができます。
[1] Off-diagonal wave function Monte Carlo studies of Hubbard model I
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 67, 3867 (1998).
[2] d-wave state with multiplicative correlation factors for the Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 68, 3608 (1999).
[3] Off-diagonal wave function Monte Carlo studies of Hubbard model II
T. Yannagisawa: Journal of the Physical Society of Japan 85, 114707 (2016).
[4] Off-diagonal wave function Monte Carlo studies of Hubbard model III
T. Yanagisawa: Journal of the Physical Society of Japan 88, 054702 (2019).
[5] Quantum Monte Carlo method for many-fermion systems
T. Yanagisawa: Physical Review B75 (2007) 224503.
| |

