量子論の世界 多体量子論 ・フェルミ液体論入門 超伝導の世界 ・超伝導現象 ・最近の超伝導研究 ・超伝導の応用 ・新超伝導体の設計 ・超伝導と素粒子論 強相関電子系 ・ハバードモデル ・変分モンテカルロ法 ・負符号問題について ・超伝導凝縮エネルギー ・電子相関と超伝導 ・ 近藤効果について ・近藤効果と重い電子 ・空間反転と物性 ・プログラム公開 ・モット相転移 ・Dirac電子と近藤効果 超伝導の研究 ・銅酸化物高温超伝導 ・高温超伝導研究 ・高温超伝導の相図 ・チェッカーボード ・高温超伝導について ・Sr2RuO4超伝導 ・価数ゆらぎ超伝導 ・擬ギャップ・超伝導 ・鉄系超伝導体 ・鉄系の同位体効果 ・多バンド超伝導 ・高温超伝導機構 ・非整数量子磁束 場の理論 ・非線型シグマモデル ・インスタントン ・サインゴルドンモデル ・南部Goldstoneボソン 数値計算物理 ・量子モンテカルロ法 ・電子対相関関数 ・ダイナミカルクラスター法 最近の論文 リンクス トップページ
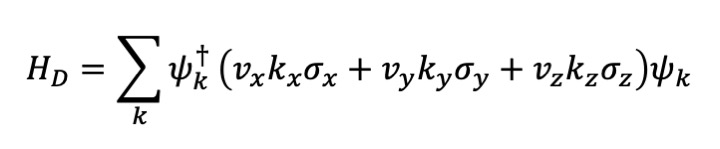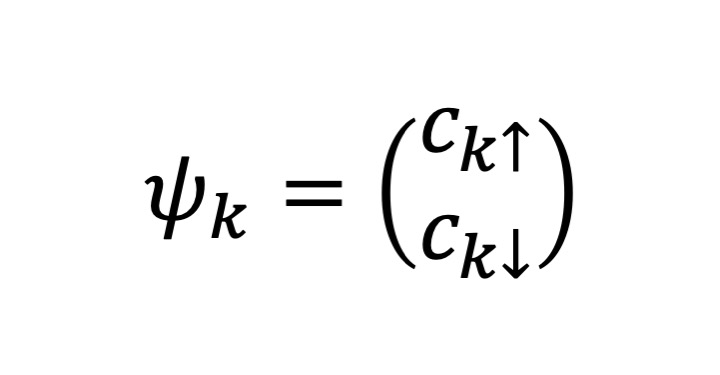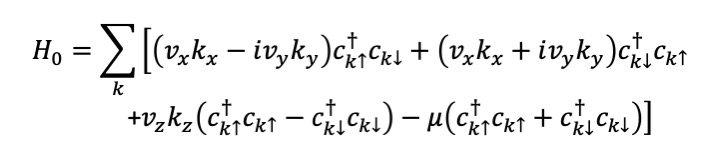
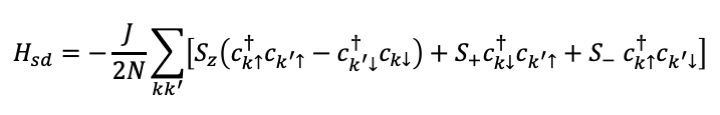
	ディラックフェルミオン系における近藤効果             　ディラックフェルミオン系に磁性不純物が存在する場合における局在スピンとフェルミオンとの相互作用について考えてみましょう。 この場合にも近藤効果が起きます。この系はスピンー軌道相互作用が存在する時の近藤効果と類似性があります。 この時、電子のエネルギーの分散は線形になり、その線形分散が物理量にどのように影響するかという問題になります。 ディラックフェルミオンはトポロジカル物質にも現れ、トポロジカル物質における近藤効果も興味ある話題です。 ディラックフェルミオンとしては次のハミルトニアンで与えられるものを考えます。 ここで、ψ は2成分の場であり、 とします。スピンアップとダウンをまとめて一つの場として表したものです。 相互作用も含めた全ハミルトニアンを H=H0+Hsd と書きますと次で与えられます。 　近藤効果においては、フェルミ面が存在することと局在スピンが内部自由度を持っていることが重要です。 近藤さんは、近藤効果に関連する現象を「フェルミ面効果」と呼んでいました。1964年の抵抗極小の論文においてすでに、 フェルミ面効果により抵抗極小が起きると書かれています。 ディラックフェルミオン系においては、フェルミエネルギーの位置に依存してフェルミ面の大きさが変化します。 それに伴い近藤温度 TK も変化します。 下の表に近藤温度 TK の表式を示します。 フェルミエネルギー μ がカットオフ（バンド幅）に比べて小さい時は、TK は |μ| に比例します。 フェルミ面が点になってしまう場合には、局在スピンに対する遮蔽が起こらず近藤効果が起きないことがわかります。 参考文献 [1] T. Yanagisawa: J. Phys. Soc. Jpn. 81, 094713 (2012) 　"Kondo effect in the presence of the spin-orbit coupling" [2] T. Yanagisawa: J. Phys. Soc. Jpn. 84, 074705 (2015) 　"Kondo effect in Dirac systems" [3] T. Yanagisawa: J. Phys. Conference Series 603, 012014 (2015)

	Condensed Matter Physics Group: Nanoelectronics Research Institute