There are three fundamental phases in the phase diagram:
the antiferromagnetic insulator phase (AFI), the coexistence state of
antiferromagnetism and superconductivity and the $d$-wave superconducting state.
The phase diagram for t' = 0 is described as follows.
When t' = 0 and U/t is as large as the bandwidth or greater than the bandwidth,
near half-filling for approximately 0 < x ≤ 0.06, the ground state is an AF insulator,
where x is the doping rate (carrier density).[4]
The AF insulator phase exists because of an instability toward the phase-separated state when t' = 0.
We have the coexistent state for 0.06 ≤ x ≤ 0.09.
When the doping rate is the range x > 0.09, the ground state is pure d-wave SC state.
The phase diagram indicates that high-temperature superconductivity may occur
in the strongly correlated region of the Hubbard model.
We have investigated the ground-state properties in the strongly correlated region of
the two-dimensional Hubbard model by using the optimization variational Monte Carlo method.
We examined the inhomogeneous ground state at 1/8 hole doping near the optimal doping region.
The strength of the on-site Coulomb repulsive interaction is chosen as U/t = 18
which is much larger than the bandwidth. This value may depend on the wave function that we use.
This critical value will decrease when we improve the wave function further by multiplying by
correlation factors.
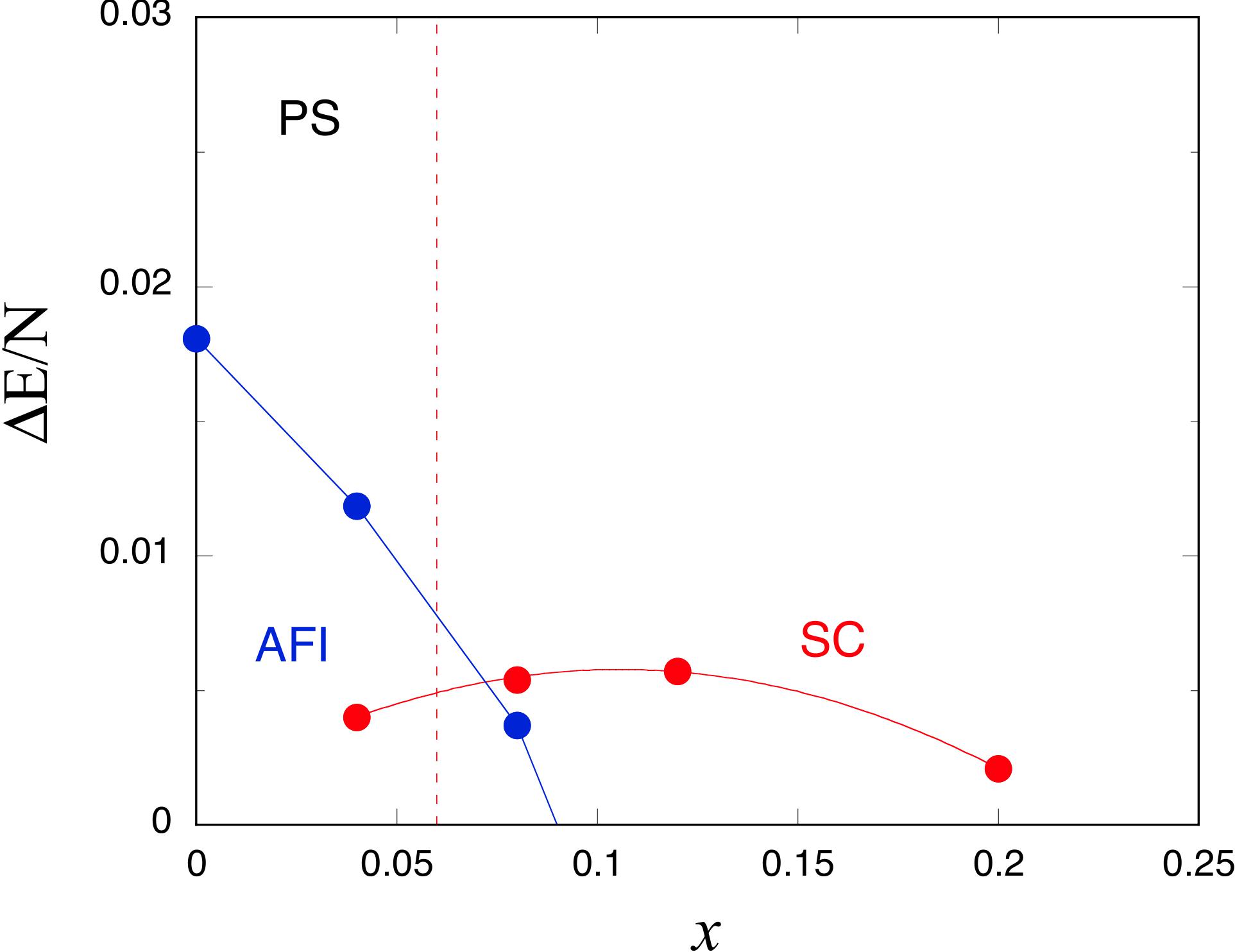
Fig. 1. Phase diagram for the two-dimensional Hubbard model.
The condensation energy per site as a function of the hole doping rate
x = 1 − ne on a 10 × 10 lattice. We set t' = 0 and U/t = 18.
The AFI indicates the antiferromagnetic insulating state and SC denotes the $d$-wave SC phase.
There is the coexistent state between these states.
The striped state is in general stable when the doping rate x is near x = 1/8.
Both the spin and charge inhomogeneous distributions are cooperated to lower the ground-state energy in stripe states.
This mechanism well works for the negative t'.
In the case of vanishing t', stripes are not stabilized when U/t is large
because the antiferromagnetic state becomes unstable and its correlation is weak for t' = 0.
Thus for t' = 0 a state with charge inhomogeneity is realized without magnetic ordering.
In Fig. 2, we show the ground-state energy as a function of Δs for several values of ρ.
The ground-state energy is the lowest at the finite value of ρ being given by ρ ≈ 0.03.
This may confirm the coexistence of inhomogeneous charge order and superconductivity.
The stability of charge inhomogeneous state may be closely related to the kinetic energy effect in superconductivity.
The kinetic energy gain along one-dimensional hole domains stabilizes the charge-ordered state.
It has been argued that the kinetic energy effect becomes important in the strongly correlated region [6].
We expect that this effect also plays an essential role in the emergence of charge inhomogeneity.
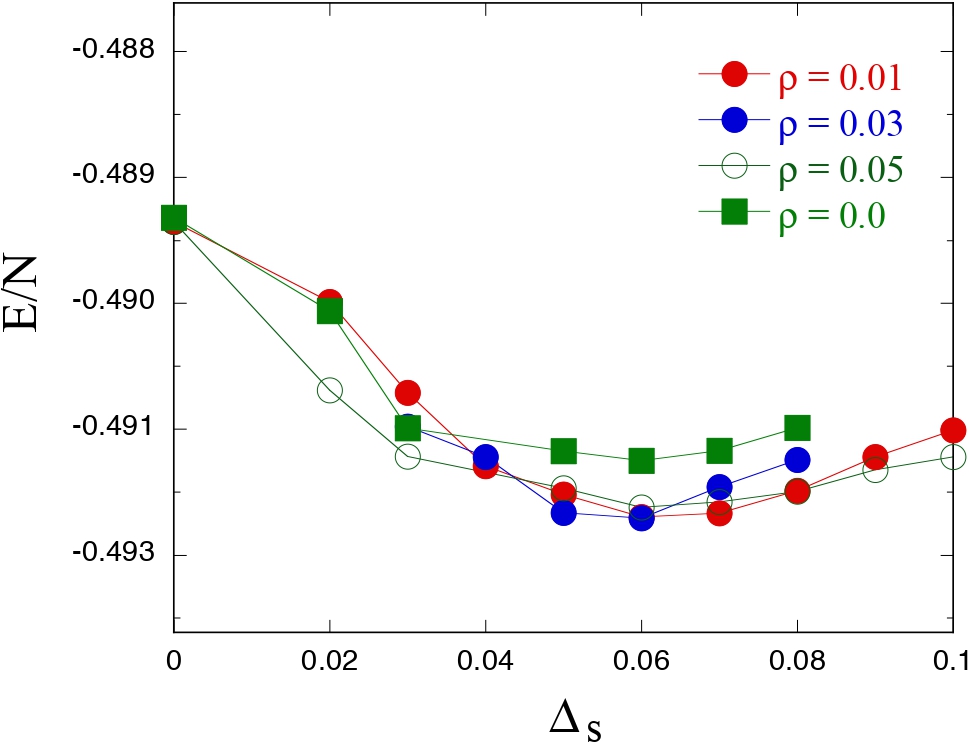
Fig. 2. The ground-state energy per site as a function of the SC gap parameter
Δs for ρ = 0.0, 0.01, 0.03 and 0.05 on a 16 × 16 lattice where
we used U = 18t, t' = 0 and Ne = 228. The variational parameters are the same
as those in Fig. 1.
Monte Carlo statistical errors are within the size of symbols.
References:
[1] T. Yanagisawa et al., J. Phys. Soc. Jpn. 67, 3867 (1998).
[2] T. Yanagisawa, Phys. Rev. B75, 224503 (2007) (arXiv: 0707.1929).
[3] T. Yanagisawa, J. Phys. Soc. Jpn. 85, 114707 (2016).
[4] T. Yanagisawa, J. Phys. Soc. Jpn. 88, 054702 (2019).
[5] T. Yanagisawa, Condensed Matter 4, 57 (2019).
[6] T. Yanagisawa, Phys. Lett. A403, 127382 (2021).
[7] T. Yanagisawa et al., EPL 134, 27004 (2021).
| |

