Let us discuss the Kondo effect when there exists a localized magnetic impurity in a system of
Dirac fermions. The interaction between Dirac fermion and the localized spin is analogous to that
in the presence of the Rashba spin-orbit coupling.
The Hamitonian of non-interacting Dirac fermions is written as
 ,
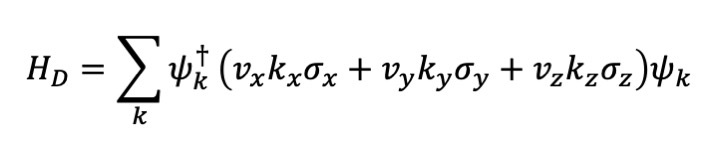where ψ represents a two-component Fermi field given by
 .
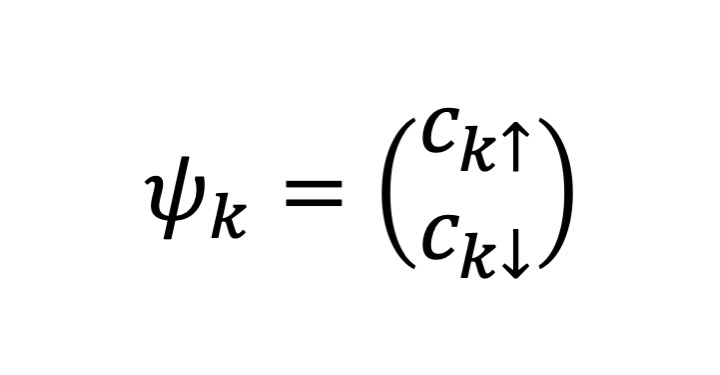The totak Hamiltonian is written as H=H0+Hsd where
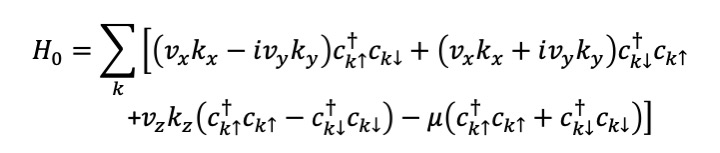
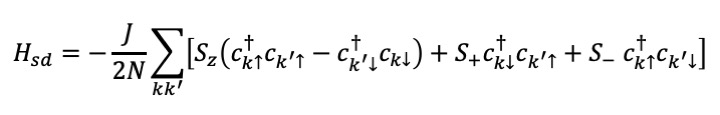
In the Kondo effect, the existence of the Fermi surface and internal degrees of freedom of
localized spins is important.
For Dirac fermions, the Fermi surface is dependent on the position of the Fermi
energy μ. The Fermi surface changes from a large Fermi surface to a small one as
the Fermi energy μ varies. The Fermi surface becomes a point at the Dirac point.
Thus the Kondo temperature TK also depends on μ.
The formulae for TK is shown in the table below.
TK is proportional to |μ| when |μ| is small as shown in the table,
ans thus TK vanishes at μ = 0 just on a Fermi point.
References:
[1] T. Yanagisawa: J. Phys. Soc. Jpn. 81, 094713 (2012)
"Kondo effect in the presence of the spin-orbit coupling"
[2] T. Yanagisawa: J. Phys. Soc. Jpn. 84, 074705 (2015)
"Kondo effect in Dirac systems"
[3] T. Yanagisawa: J. Phys. Conference Series 603, 012014 (2015)
"Dirac fermions and Kondo effect"
| |
