Holes doped in a half-filled square lattice lead to an incommensurate spin and charge-density wave.
Recently, it has been experimentally found that the stripe order is stabilized in a wide underdoped
region of La2-xSrxCuO4 (LSCO) at low temperatures.
From the experiment of resistivity in the light-doping region of LSCO, the system has a metallic
behavior below the antiferromagnetic transition temperature, that is considered to originate in the
formation of metallic charge stripes.
We performed the variational Monte Carlo calculations to the 2D Hubbard model for U=8.
In the lower doping region, the relationship of the hole density and incommensurability,
&delta &sim x, is satisfied.
[1][2]
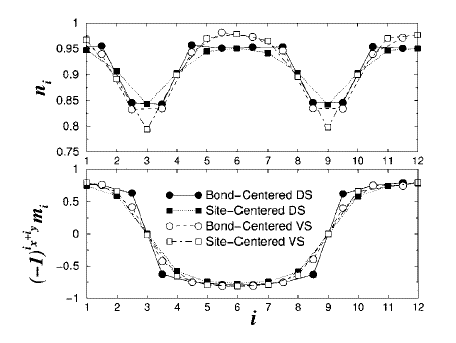
Fig.1. Spatial dependence of charge density and staggered magnetization. [1,2]
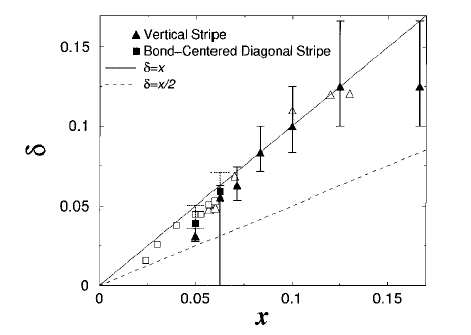
Fig.2. Incommensurability vs Carrier density. [1]
A checkerboard-like charge-density modulation with a roughly 4a × 4a period
(a is the lattice spacing) has also been observed by scanning tunneling microscopy
(STM) experiments in Bi2Sr2CaCu2O8+&delta (Bi-2212),
Bi2Sr2-xLaxCuO6+&delta and Ca2-xNaxCuO2Cl2 (Na-CCOC).
To examine the stability of a 4 × 4checkerboard state,
we have performed a variational Monte Carlo simulation on a two-dimensional
t-t'-t''-U Hubbard model with a Bi-2212 type band structure.
[3]
The striped incommensurate spin-density wave state (ISDW) is defined by a single Q vector.
On the other hand, the checkerboard ISDW state is described by the double-Q set.
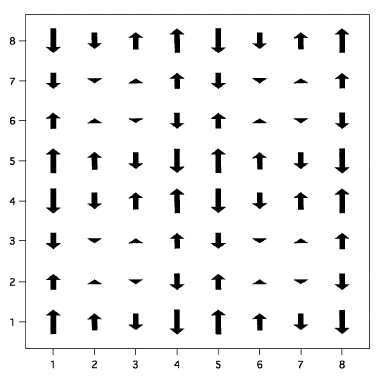
Fig.3. Checkerboard stete. [3]
We found that the coexistent state of bond-centered four-period diagonal and
vertical spin-checkerboard structure characterized by a multi-Q set is stabilized and
composed of 4 × 4 period checkerboard spin modulation by using the variational
Monte Carlo method.
This state can be understood as an incommensurate spin density wave enhanced by
Fermi surface nesting, which appears in the precursory peaks of spin susceptibility
at (&pi,&pi), (&pi/2,&pi) and (&pi/2,&pi/2).
From VMC compuations, we have confirmed that the Fermi surface with larger t'/t and flat-section near zone edges are
required for the stabilization of the 4× 4 checkerboard state.
The checkerboard structure is induced by the nesting between the flat parallel zone edges. [5]
References
[1] Diagonal Stripe States in the Light-Doping Region in the Two-Dimensional Hubbard Model
M. Miyazaki, T. Yanagisawa, K. Yamaji: Journal of the Physical Society of Japan 73 (2004) 1643.
[2] Stripe formation in high-Tc superconductors
T. Yanagisawa, S. Koike, M. Miyazaki, K. Yamaji: Journal of Phyisics: Condensed Matter 14 (2002) 21.
[3] Checkerboard States in the Two-Dimensional Hubbard Model with the Bi2212-Type Hubbard Model
M. Miyazaki, K. Yamaji, T, Yanagisawa, R. Kadono: Journal of the Physical Society of Japan 78 (2009) 043706.
[4] Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional Hubbard model
T. Yanagisawa, M. Miyazaki, K. Yamaji: Journal of the Physical Society of Japan 78 (2009) 013706.
[5] M. Miyazaki, K. Yamaji, T. Yanagisawa, R. Kadono: Physica C470 (2010) S919.
| |

