Correlated Electrons ・Hubbard model ・Variational M.C. ・Negative sign ・Superconductivity ・Kondo effect ・Spatial Inversion ・Mott transition Superconductivity ・Cuprate HTSC ・Research HTSC ・Condensation Energy ・Phase diagram ・Checkerboard ・On HTSC ・Pseudogap HTSC ・Valence skip ・Fe pnictide ・Fe isotope effect ・Sr2RuO4 ・Multiband super ・Fractional vortex ・Origin of HTSC Field Theory ・Nonlinear sigma model ・Skyrmion, spin vortex ・Sine-Gordon model Computational Physics ・Quantum Monte Carlo ・Pair correlation function ・Dynamical Cluster method Publication Links Home
	Superconductivity in the Hubbard Model             Let us investigate the origin of superconductivity on the basis of the model with electronic interactions. 　The Hubbard model for small U is mapped onto an effective Hamiltonian Heff = eSHe-S,with the attractive interaction, using the canonical transformation [1,2]. This means that the Hubbard model contains an attractive channel for electrons. The gap equation of the weak coupling formulation can be solved without numerical ambiguity to determine the symmetry of Cooper pairs. We have determined the symmetry of Cooper pairs, on the basis of Heff, for the two-dimensional Hubbard model. The superconducting gap crucially depends on the position of the van Hove singularity (Fig.1). We presented the phase diagram in the plane of the electron filling ne and the next nearest-neighbor transfer t'. The d-wave pairing is dominant for the square lattice in a wide range of ne and t'. The d-wave pairing is also stable for the square lattice with anisotropic t'. The three-band d-p model was also investigated, for which the d-wave pairing is stable in a wide range of ne and tpp (the transfer between neighboring oxygen atoms). In relation to cuprate superconductors, the second-neighbor transfer parameter -t' could not be so large so that the optimum doping rate is in the range of 0.8 < ne < 0.85 in the weak-coupling analysis. 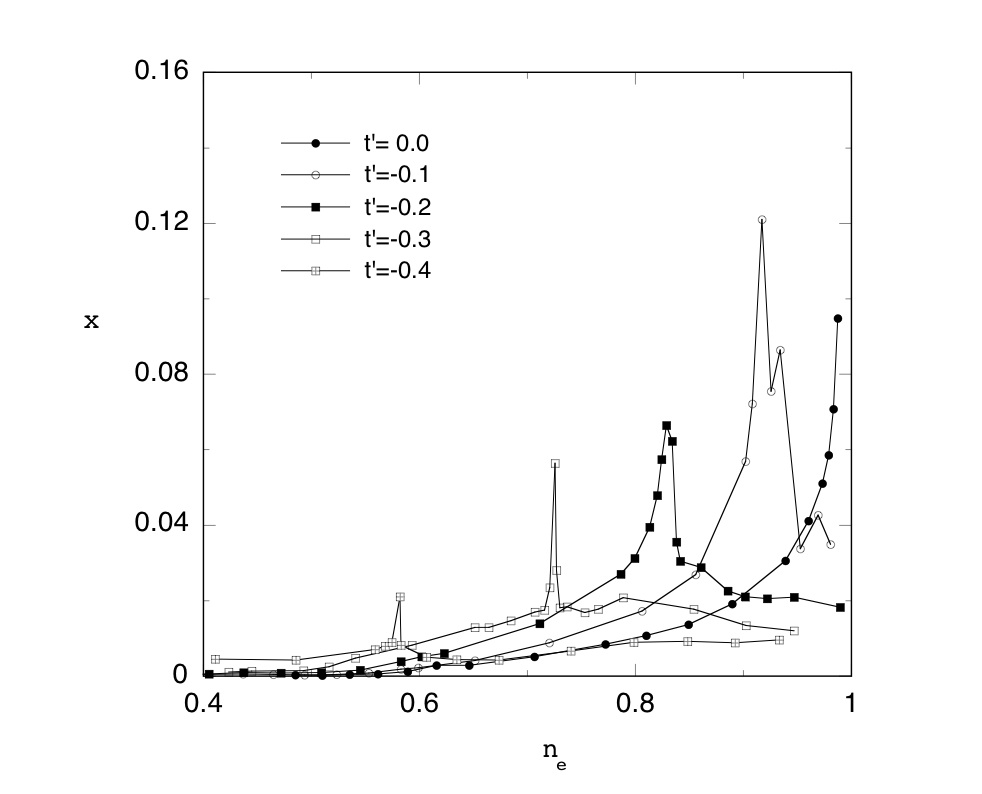Fig.1. The exponent x of the pairing state with dx2-y2 symmetry as a function of the electron density ne for t' = 0, -0.1, -0.2, -0.3 and -0.4. The gap function &Delta is related to x as &Delta = t exp(-2t2/(xU2)). 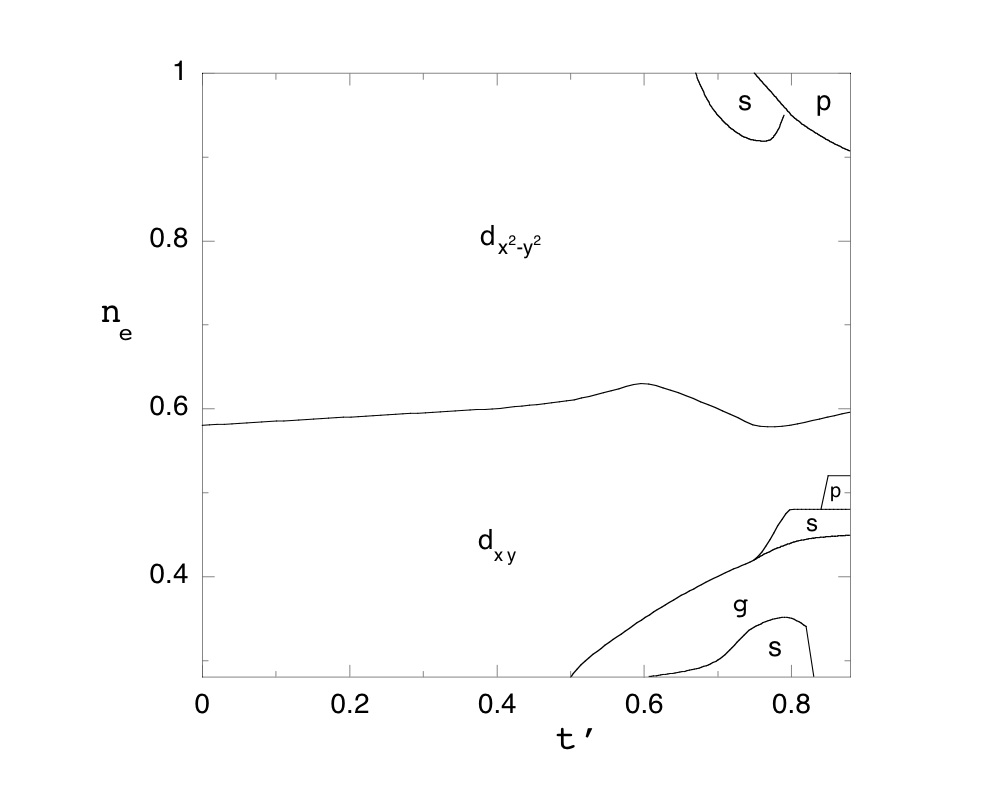Fig.2. Phase diagram of the effective Hamiltonian Heff of the two-dimensional Hubbard model with t'<0. t' is the next nearest-neighbor transfer integral. 　 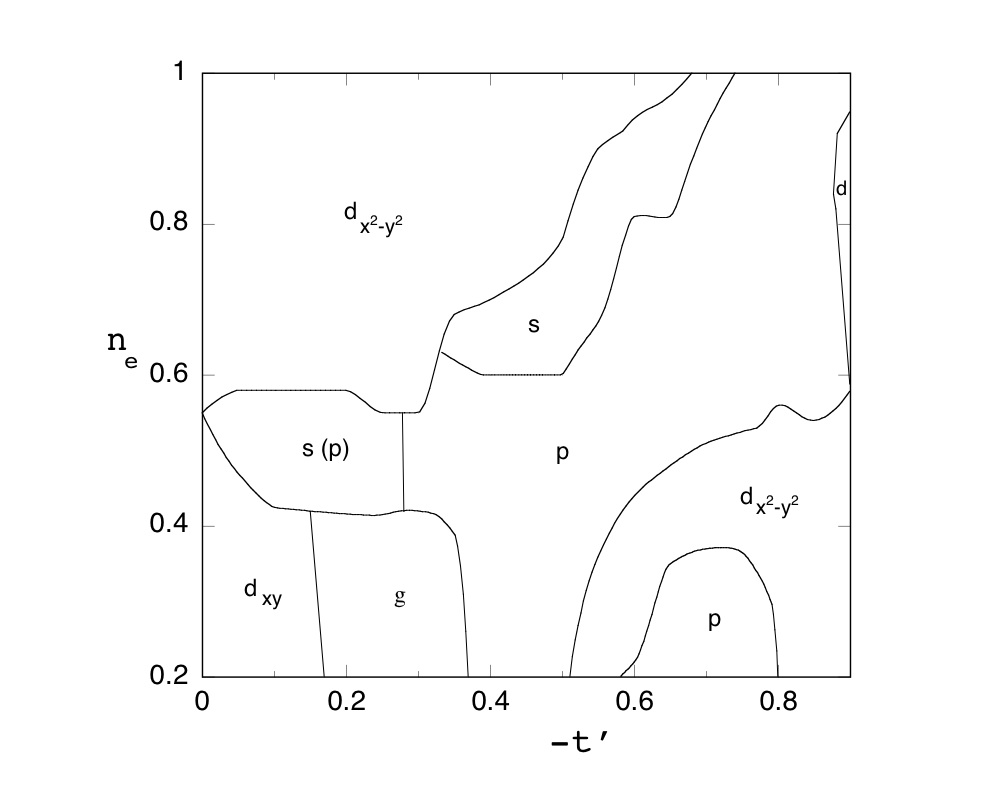Fig.3. Phase diagram of the effective Hamiltonian Heff of the two-dimensional Hubbard model with t'>0. 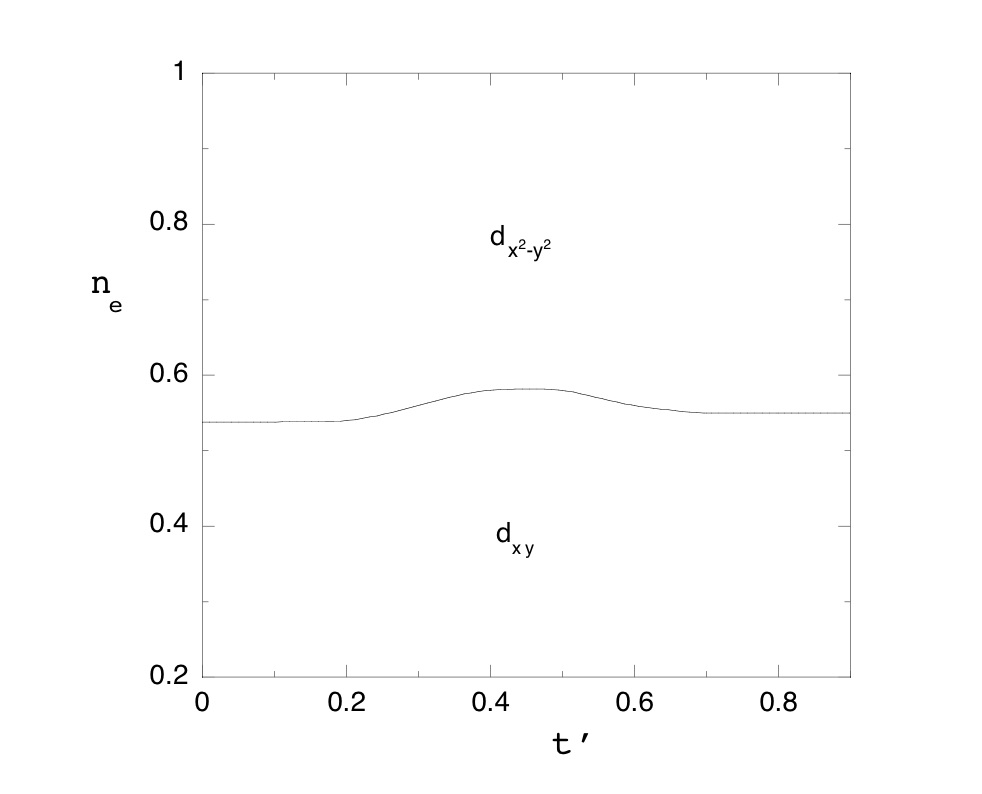Fig.4. Phase diagram of the effective Hamiltonian Heff of the two-dimensional Hubbard model on the anisotropic triangular lattice (model for organic conductors). We set t'>0. [1] J. Kondo: J. Phys. Soc. Jpn. 70 (2002) 808. [2] T. Yanagisawa: New J. Phys. 10 (2008) 023014.

	Condensed Matter Physics: Electronics Research Institute