A quantum Monte Carlo method is a method to calculated physical quantities numerically in correlated electron systems.
Let H be the Hamiltonian. Then the ground-state wave function is written as
ψ = e−λ H ψ0,
where ψ0 is an initial wave function such as the Fermi sea.
When λ is large enough, the exponential factor e−λ H will extract the ground-state wave function
from ψ0.
We write this wave function in the form
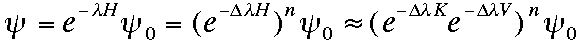
where the Hamiltonian H is divided into
H = K+V
and we put λ = nΔ λ.
K is the non-interacting part of the Hamiltonian and V is the interaction term.
We usually use the Hubbard-Stratonovich transformation to write the interaction V
in a bilinear form. This results in a summation with respect to huge number of Hubbard-Stratonovich variables.
We calculate expectation values for this wave function numerically in a quantum Monte Carlo method.
We, however, sometimes encounter the negative sign problem in this procedure.
We proposed an optimization quantum variational Monte Carlo method for the wave function ψ ([1− 4]).
We write the wave function in the form
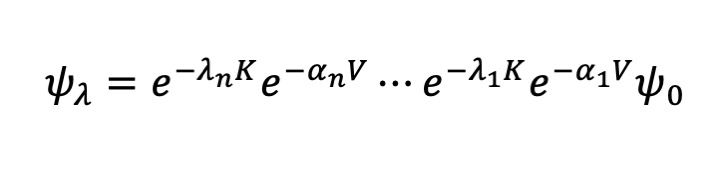Here λj and αj (j = 1, …, n) are variational parameters.
(We called this wave the off-diagonal wave function in a series of papers.)
This wave function can be regarded as a generalization of that used in a quantum Monte Carlo simulation ψ.
ψ is a special case of ψλ where λj and αj are all the same.
when we treat λj and αj as variational parameters so that the ground-state energy has a minimum,
the negative sign is reduced and it never becomes a problem [2].
The sign does not show up a problem when the ground state wave function is optimized.
In an expanded space of wave functions, the negative sign is not serious and we can approach the exact ground-state
wave function.
(We call the wave function ψλ the off-diagonal wave function.
This is because this wave function is in contrast to wave functions of Jastrow and Gutzwiller type.
We take into account site-diagonal correlations using Jastrow and Gutzwiller wave functions.
In stead, we can consider site off-diagonal correlations between electrons for ψλ.)
We have also developed an alternative optimization method on the basis of the Quantum Monte Carlo algorithm [5].
Typically, the ground-state wave function is defined as
ψ = e−λ Hψ0,
where H is the Hamiltonian and ψ0 is the initial one-particle state such as the Fermi sea.
In the quantum Monte Carlo method this wave function is written as a
linear combination of the basis states, generated using the Hubbard-Stratonovich transformation; that is
ψ = ∑mcmφm.
There are several ways to treat this wave function.
In the standard method, as is well known, we use the Metropolis algorithm to evaluate the expectation values.
In stead, here, we present an alternative algorithm.
From the variational principle, the coefficients cm are determined
in the selected subspace {φm} to calculate the ground-state energy and other quantities.
We denote the number of states in this subspace as Nstates.
If the expectation values are not highly sensitive to the number of basis states, we can obtain correct
expectation values by using an extrapolation in terms of the number of basis states at the limit
Nstates → ∞.
References:
[1] Off-diagonal wave function Monte Carlo studies of Hubbard model I
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 67, 3867 (1998).
[2] d-wave state with multiplicative correlation factors for the Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 68, 3608 (1999).
[3] Off-diagonal wave function Monte Carlo studies of Hubbard model II
T. Yannagisawa: Journal of the Physical Society of Japan 85, 114707 (2016).
[4] Off-diagonal wave function Monte Carlo studies of Hubbard model III
T. Yanagisawa: Journal of the Physical Society of Japan 88, 054702 (2019).
[5] Quantum Monte Carlo method for many-fermion systems
T. Yanagisawa: Physical Review B75 (2007) 224503. PDF
References on QMC
[6] J. E. Hirsch: Phys. Rev. Lett. 51 (1983) 1900.
[7] J. E. Hirsch: Phys. Rev. B31 (1985) 4403.
[8] S. Sorella et al.: Int. J. Mod. Phys. B2 (1988) 993.
[9] S. R. White et al.: Phys. Rev. B40 (1989) 506.
[10] M. Imadda et al.: J. Phys. Soc. Jpn. 58 (1989) 3752.
[11] E. Y. Loh et al.: Phys. Rev. B41 (1990) 9301.
[12] A. Moreo et al.: Phys. Rev. B56 (1991) 11442.
[13] A. Moreo: Phys. Rev. B45 (1992) 5059.
[14] S. Fahy and D. R. Hamann: Phys. Rev. B43 (1991) 765.
[15] S. Zhang et al.: Phys. Rev. B55 (1997) 7464.
| |
