The nonlinear sigma model has some universality.
It plays an important role in every physics.
The model is given by the action:
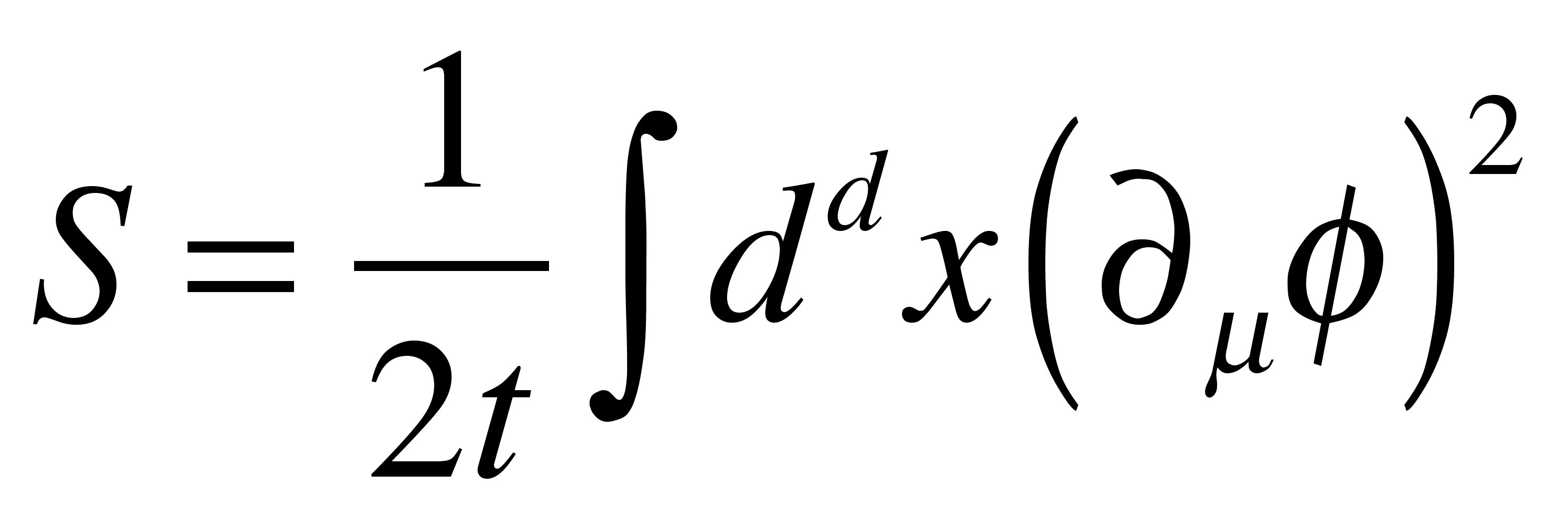
Here, φ is an N-component scalar field satisfying φ²=1.
The parameter t indicates the temperature.
In two dimensions the 0(3) nonlinear sigma model shows asymptotic freedom and has an analogy to the
4D non-abelian gauge theory. It also has an analogy with quark confinement, and also with the Kondo effect.
The 0(3) nonlinear sigma model has an instanton solution ([1][2][3]), which is also an analogy with the 4D non-abelian
gauge theory ([4][5]).
The nonlinear sigma model, obtianed as a continuum limit of the classical Heisenberg model, describes
spin-wave excitation model at low temperatures.
Because a d-dimensional quantum system is equivalent to a (d+1)-dimensional quantum system, the d-dimensional quantum
Heisenberg model is mapped to the (d+1)-dimensional nonlinear sigma model.
In fact, the correlation function 〈 Si⋅ Sj〉 for the 2D quantum antiferromagnetic Heisenberg model,
calculated by using the spin-wave theroy, is the same as that for the (2+1)D nonlinear sigma model [6].
This model exhibit asympototic freedom at high temperatures (high energy region), and has a fixed point at absolute zero T = 0 [6].
This is analogous to phenomena of the Kondo effect and quark confinement.
The action of (d+1)D nonlinear sigma model is
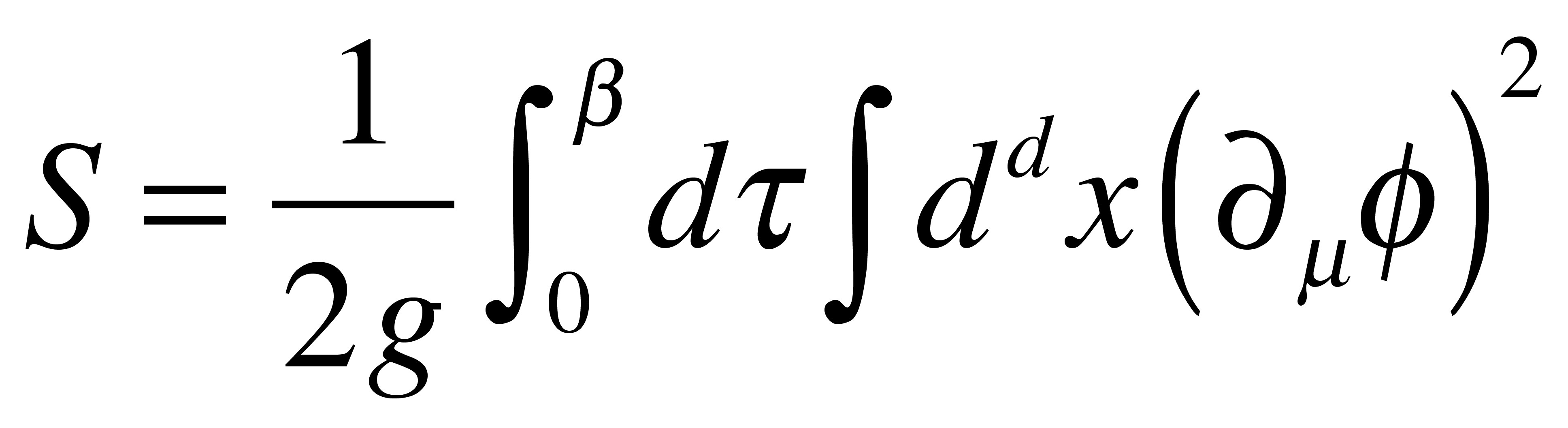
It is known that the correlation length of the 2D nonlinear sigma model ξ increases exponentially at low temperatures:
ξ ∼ C (T/2π ) exp(2π /T) ([7][8]).
The correlation length of the (2+1)D model also shows an exponential nehavior ([6][9]):
ξ ∼ Cξexp(2π JF/T).
The quantum effect creduces the constant F in this formula.
Monte Carlo simulation indicated F = 0.22 and the two-loop renormaliozation group gives [6]
F = 0.26.
The agreement between two method is very good.
References:
[1] A.A. Belavin and A.M. Polyakov: JETP Lett. 22, 245 (1975).
[2] V.A. Fateev, I.V. Frolov, A.S. Schwarz: Nuclear Physics B154, 1 (1979).
[3] B. Berg and M. Lü scher: Comm. Math. Phys. 69, 57 (1979).
[4] A.A. Belavin, A.M. Polyakov, A.S. Achwarz, Y.S. Tyuokin: Phys. Lett. B59, 85 (1975).
[5] G. 'tHooft: Phys. Rev. D14, 3432 (1976).
[6] T. Yanagisawa: Renormalization of the quantum antiferromagnet in two dimensions: Phys. Rev. B46, 13896 (1992).
[7] S.H. Shenker and J. Tobochnik: Phys. Rev. B22, 4462 (1980).
[8] Y. Iwasaki: Prog. Theor. Phys. 68, 448 (1982).
[9] S. Chakravarty, B.I. Halperin, D.R. Nelson: Phys. Rev. B39, 2344 (1989).
| |

