We can evaluate the expectation value exactly for correlated wave functions using a variational Monte Carlo method.
The variational Monte Carlo is applicable from weaky correlated to strongly correlated regions without a negative sign problem.
The variational Monte Carlo method is based on the variational principle shown below:
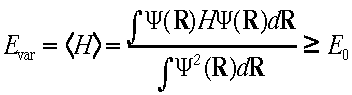
A simple wave function is given by an ansatz of Gutzwiller; we multiply the Gutzwiller projection operator to the one-body wave function:
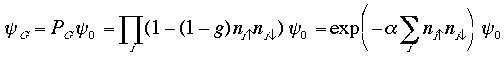
With this simple wave function, we can extract many interesting properties of the ground state of strongly correlated systems.
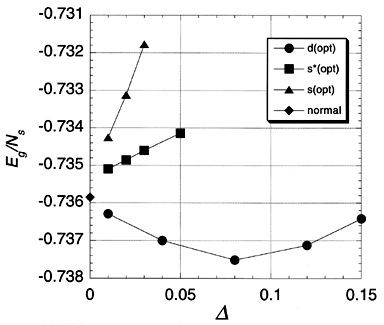
Fig.1 Ground-state energy obtained by VMC.
The figure shows the ground-state energy as a function of the superconducting (SC) order parameter Δ where the calculations were carried out on the 10×10 lattice and the strength of the on-site Coulomb repulsion is U = 8. We found a minimum at a finite value of the SC order parameter with d-wave symmetry, which shows a possibility of superconductivity in the Hubbard model. This result was surprising for us at that time.
References:
T. Nakanishi et al.: J. Phys. Soc. Jpn. 66 (1997) 294.
K. Yamaji et al.: Physica C304 (1998) 225-238.
It is necessary to improve the wave function beyond the Gutzwiller ansatz.
One way is to take account of intersite electron correlation such as doublon-holon correlation by
employing the Jastrow correlation factor. In the other way, we can borrow the idea used in quantum Monte
Carlo method.
In the quantum Monte Carlo method, the exact ground-state wave function is given by the following formula:
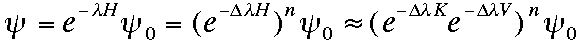
This formula indicates that the wave function is improved by multiplying exponential factors repeatedly to a trial function. We show the ground-state energy for the half-filled Hubbard model based on the improved wave function in the figure below. Circles indicate the results obtained uisng Qyantum Monte Carlo method.
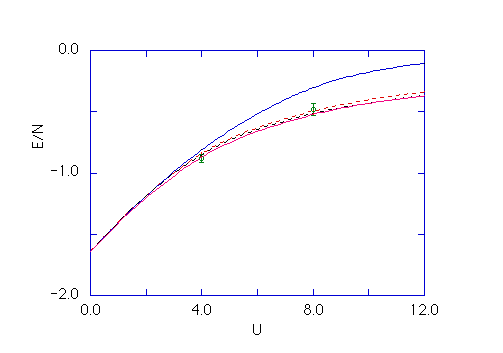
Ref. T. Yanagisawa et al.: J. Phys. Soc. Jpn. 67 (1998) 3867.
| |

