There are solutions of vortices with fractionally quantized flux in multiband superconductors.
The existence of fractionally quantized-flux vortices is very interesting and attractive.
The phases of gap functions are important and the kink (soliton) solution of phase difference plays a central role
for the existence of fractional flux vortices.
In a two-band model, the half-quantum-flux vortex exists at the edge of a line singularity of the phase
variables (see Fig.1 where θ denotes the phase of the gap Δ1). θ changes from 0
to π across the singularity, while the phase θ2 of the gap Δ2 changes
from 0 to -π. In two regions above and below the singularity line, the phase difference
θ1-θ2 is 0 mod 2π. Thus the energy costs due to Josephson couplings are
the same there. In the case of Fig.1, a net-change of θ1 is 2π by a counterclockwise
encirclement of the vortex, and that of θ2 vanishes. This results in a half-quantum flux vortex.
The existence of a half-flux vortex in triplet superconductors have also been predicted [3].
A generalization to a three-gap superconductor is not trivial.
We have very attractive features, that is, chiral states with time-reversal
symmetry breaking and the existence of fractionally quantized vortices.
Further, in the case with more than four gaps, a new state is predicted with a gapless excitation mode.
There are many types of kinks connecting two minima of the potential in three-band superconductors.
In a three-band model, a fractional vortex has two line singularities (kinks) in the phase of the gap functions.
Two vortices can form a molecule by two kinks. Three-vortex bound states are also formulated, corresponding
to baryons when we regard the magnetic flux as charge.[1]
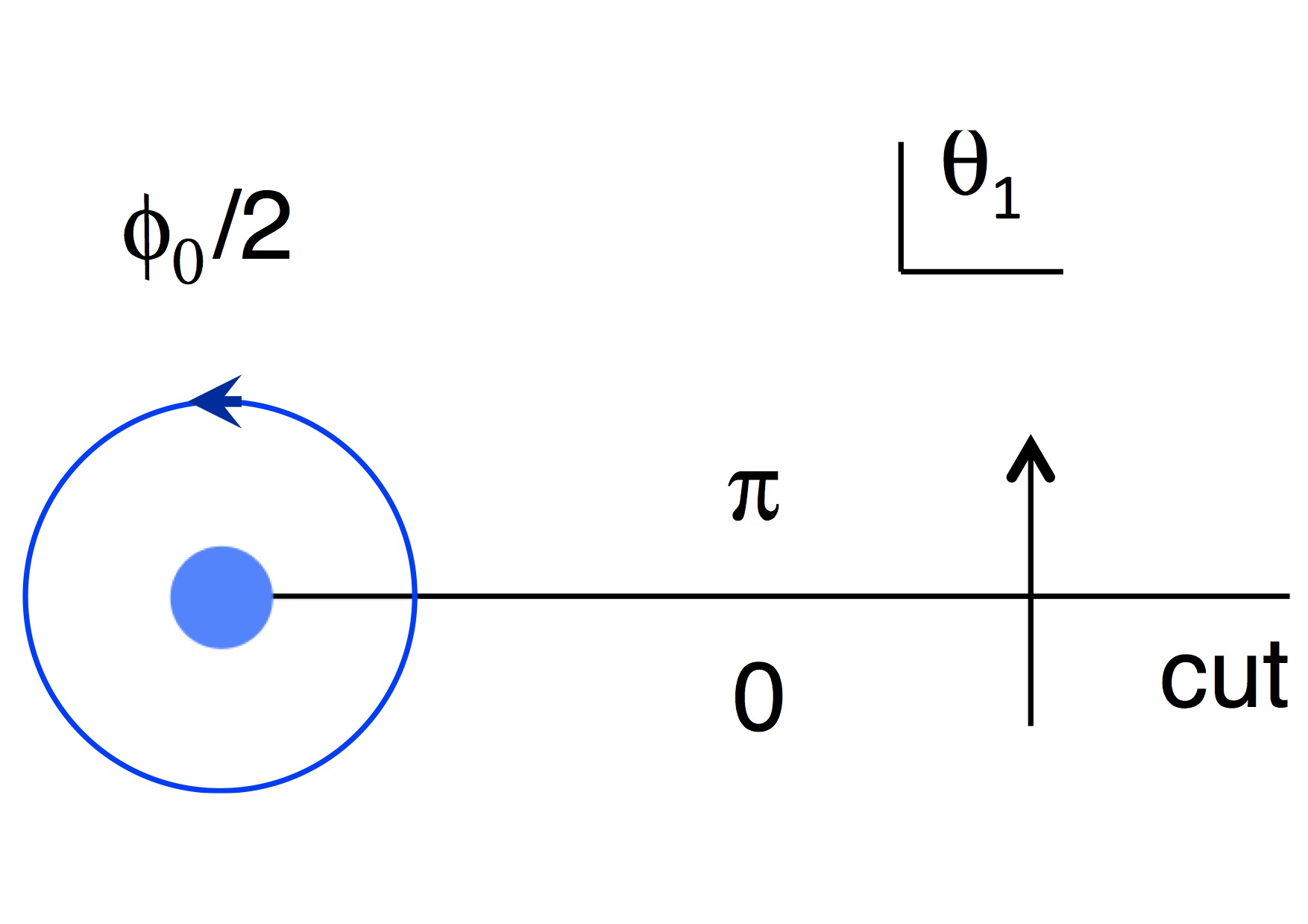
Fig.1. Half-flux vortex and a singularity of the phase variable θ1.
References:
[1] T. Yanagisawa et al.: J. Phys. Soc. Jpn. 81, 024712 (2012).
[2] Yu. A. Izyumov and V. M. Laptev: Phase Transitions 20, 95 (1995).
[3] G. E. Volovik: J. Exp. Theor. Phys. Lett. 70, 792 (1999).
| |

