The two-dimensional plane in cuprate high-temperature superconductors is modeled as the two-dimensional d-p model.
Fig.1. 2D d-p model. Blue and green circles denote copper and oxygen atoms, respectively.
We have investigated the ground state of the two-dimensional (2D) d-p model by using the variational Monte Carlo method.
The superconducting condensation energy obtained for the Gutzwiller functiion is shown below.
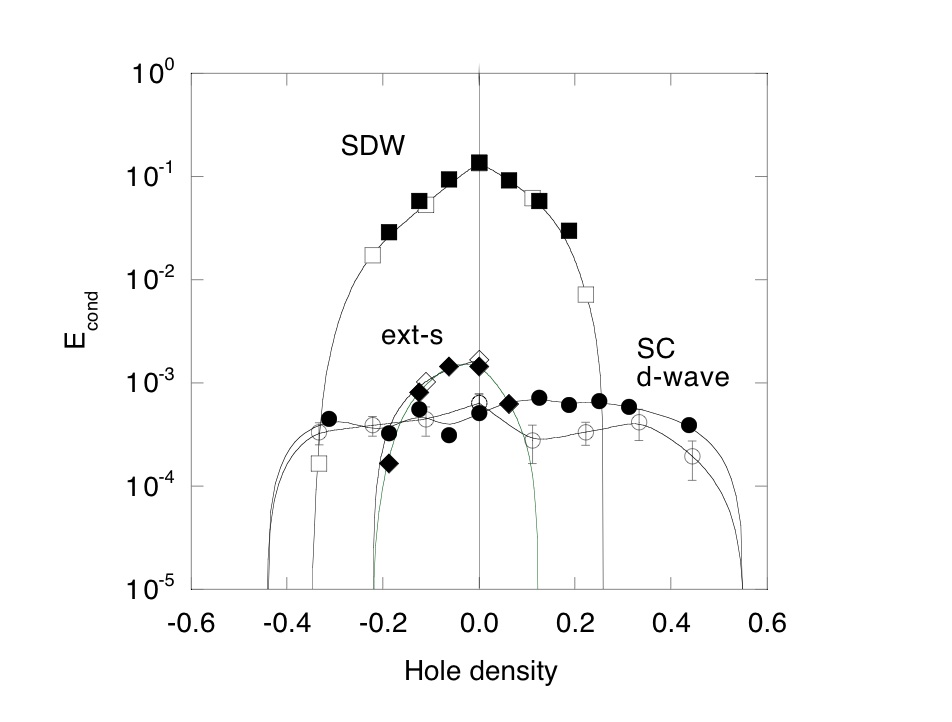Fig.2. Phase diagram of the 2D d-p model based on the variational Monte Carlo method for 6× 6、8× 8 lattices.
（Open symbols are for 8× 8 lattice.） There is a region of the extended-s wave pairing near the
half-filled case (undoped case) if the antiferromagnetic order is suppressed.
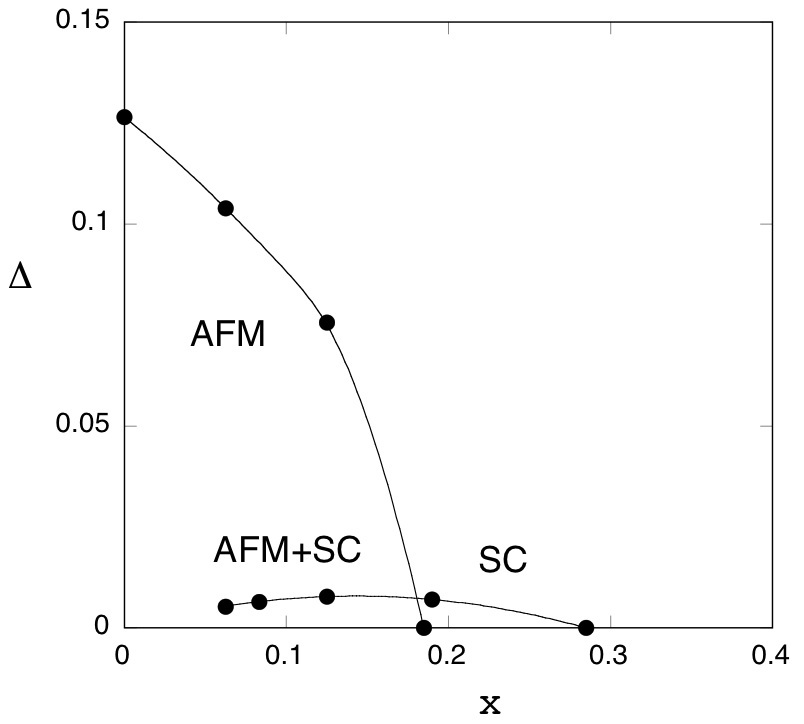
Fig. 3. Phase diagram of the 2D d-p model obtained by an extrapolation to the bulk limit, where we have also examined the coexistence state of superconductivity and antiferromagnetism. [2]
Numerical studies of the two-dimensional d-p model using the Gutzwiller ansatz have exhibited
the incommensurate antiferromagnetic state coexisting with superconductivity in the under- and light-doping regions.
We have carried out the Monte Carlo calculations up to 16 × 16 sites (768 atoms in total).
In the overdoped region in the range of 0.18 < x < 0.28, we have the uniform d-wave pairing state as the ground state.
The periodicity of spatial variation increases, as the doping rate x decreases, proportional to 1/x.
In Fig.3 we have the 12-lattice periodicity at x = 0.08333 and 16-lattice periodicity at x = 0.0625.
For x = 0.2, 0.125 and 0.08333, the results strongly suggest a finite condensation energy in the bulk limit.
The phase diagram for the hole-doped case is consistent with recent results reported for layered high temperature cuprates.
References
[1] Gorund state of the three-band Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Physical Review B64, 184509 (2001).
[2] Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model
T. Yanagisawa, M. Miyazaki, K. Yamaji: Journal of the Physical Society of Japan 78 (2009) 013706.
[3] A. Tsukada, Y. Krochenberger, M. Noda, H. Yamamoto, D. Manske, L. Alff, M. Naito: Solic State Commun. 133 (2005) 427.
| |
