The superconducting condensation energy in the BCS theory is the energy gain due to the formation of paired sate:
Econd = (1/2)VN(0)Δ2,
where Δ is the magnitude of the order parameter, N(0) is the density of states at the Fermi surface and
V is the volume of the system..
The condensation energy can be estimated from the specific heat data. The formula is
Econd = Ωn− Ωs
= ∫ (Sn− Ss) dT
= ∫ (Cs− Cn) dT
where the integral is over the interval [0, Tc]. S and C denote the entropy and the specific heat,
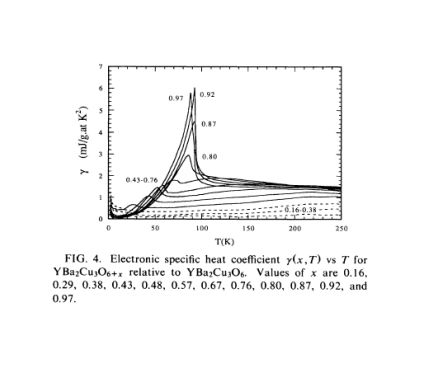
respectively. The good specific heat data have been reported for optimally doped YBCO in Ref.[1].
We computed the superconducting condensation energy per unit cell by intergrating the temperature dependent specific heat data in
Ref.[1] (shown below) numerically [3]:
Econd ≈ 0.2 meV.
To be more precisely, the integrated value is in the range of 0.17 to 0.26meV.
This can be regarded as the characteristic energy scale of cuprate high temperature superconductors.
We have carried out the variational Monte Carlo computations to estimate the condensation energy in strongly
correlated electron systems [2− 6]. We obtained the condensation energy per site as Econd ≈ 0.2 meV,
using the Gutzwiller ansatz.
This is in good agreement with the experimental value. We show the size dependence of the condensation energy in
Fig.2 (below) [5, 6].
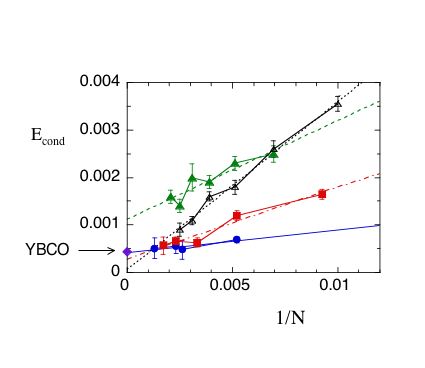
Fig. 2. Superconducting condensation energy per site as a function of 1/N where N is the
number of atoms [5]. Triangles are for the single-band Hubbard model; the hole density x = 0.86, t' = − 0.2 and
U = 8 for solid symbols, and x = 0.84, t' = − 0.15 and U = 8 for open symbols (energy unit is the nearest-neighbor transfer
integral t). Here U is the strength of the on-site Coulomb interaction and t' is the next nearest-neighbor transfer parameter.
Squares are for x = 0.2, tpp/tdp = 0.4 and Ud/tdp = 8 for the d-p model
(three-band Hubbard model), where tdp and tpp are transfer integrals between d and p orbitals and
neighboring p orbitals in the d-p model, respectiely. Ud denotes the Coulomb repulsive interaction on Cu atoms.
References
[1] J. W. Loram et al.: Phys. Rev. Lett. 71 (1993) 1740.
[2] T. Nakanishi, T. Yanagisawa, K. Yamaji: J. Phys. Soc. Jpn. 66 (1997) 294.
[3] K. Yamaji, T. Yanagisawa, T. Nakanishi, S. Koike: Physica C304 (1998) 225.
[4] T. Yanagisawa, S. Koike, K. Yamaji: Phys. Rev. B64 (2001) 184509.
[5] T. Yanagisawa, M. Miyazaki, S. Koikegami, S. Koike, K. Yamaji: Phys. Rev. B67 (2003) 132408.
[6] T. Yanagisawa, M. Miyazaki, K. Yamaji: J. Phys. Soc. Jpn. 78 (2009) 013706.
| |

