The negative sign problem in a quantum Monte Carlo (QMC) simulation is an important issue in the study of many-fermion systems.
The negative sign occurs due to fermionic property of particles, that is, we have a negative sign when two fermionic particles are exchanged. We show some results on the sign problem using an optimized wave function.
In a quantum Monte Carlo simulation the following wave function is usually used:
 ,
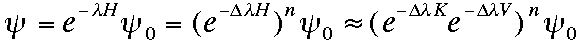where λ = nΔλ. The negative sign appears from exponential operators.
The wave function used in an optimized wave function Monte Carlo method is given as
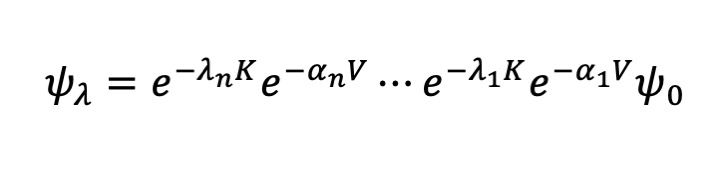Here λj and αj (j = 1, …, n) are variational parameters.
This wave function can be regarded as an generalization of that used in a quantum Monte Carlo simulation ψ.
ψ is a special case of ψλ where λj and αj are all the same.
We can show that the negative sign is reduced when we treat λj and αj as variational parameters to minimize the ground-state energy.
We show this in Fig. 1 where the ground-state energy E and the sign are presented, where the sign indicates the expectation value 〈 s 〉 of the sign s of determinants appearing in Monte Carlo steps. The calculations were carried out for the two-dimensional Hubbard model at the electron filling 0.8.
The sign problem means 〈 s 〉 → 0 for which the expectation values of physical quantities cannot be evaluated definitely.
The result in Fig. 1 indicates that the sign does not show up a problem when the ground state wave function is optimized,
and we have even 〈 s 〉 ≈ 1 for the fully optimized case.
In Fig. 1 the case E corresponds to ψ in a QMC simulation, where we cannot obtain the energy.
The value of E in Fig. 1 was obtained through an extrapolation using the values for A, B, C and D cases.
In the optimization procedure of the wave function ψ, the negative sign is not serious and we can avoid the negative sign problem. In an expanded space of wave functions we can approach the exact wave function by avoiding the negative sign.
The other advantage of this method is that we can treat the system from weakly correlated region to the strongly correlated region.
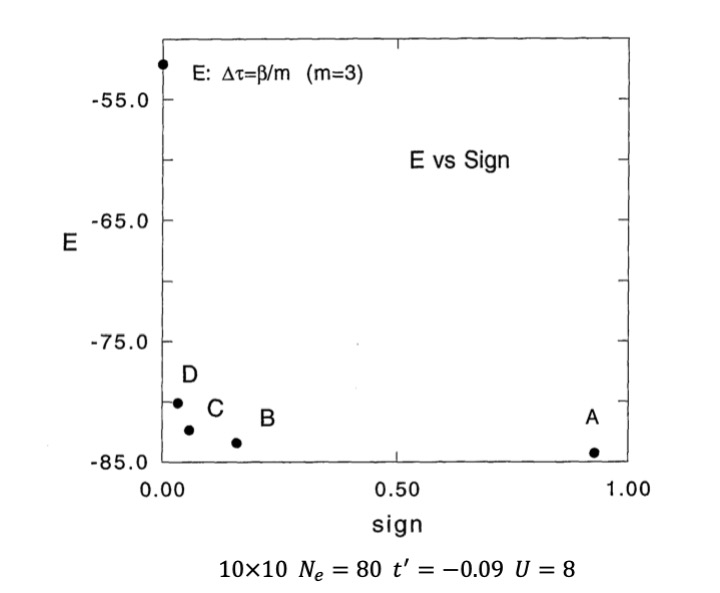
Fig.1. Ground-state energy and the sign ([2]).
References
[1] Off-diagonal wave function Monte Carlo studies of Hubbard model I
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 67, 3867 (1998).
[2] d-wave state with multiplicative correlation factors for the Hubbard model
T. Yanagisawa, S. Koike, K. Yamaji: Journal of the Physical Society of Japan 68, 3608 (1999).
[3] Off-diagonal wave function Monte Carlo studies of Hubbard model II
T. Yannagisawa: Journal of the Physical Society of Japan 85, 114707 (2016).
[4] Off-diagonal wave function Monte Carlo studies of Hubbard model III
T. Yanagisawa: Journal of the Physical Society of Japan 88, 054702 (2019).
p
| |
