|
|
| |
水晶振動子マイクロバランス法
（Quartz Crystal Microbalance）
（Sauerbreyの式）
水晶振動子マイクロバランス法においては、水晶振動子の発信を利用して、物質の吸着量をナノグラムの精度まで計測できる方法です。
水晶振動子は交流により厚み剪断（すべり）振動を起こし、一定の振動数で振動します。振動数（周波数）は水晶の厚みに依存し、
水晶振動子の電極に物質が付加されると出力周波数が変化します。付着物の質量が増大すると出力周波数が減少しますが、
この減少は付着質量に比例することが知られています[1]。振動数変化は次の式により表されます (Sauerbreyの式):
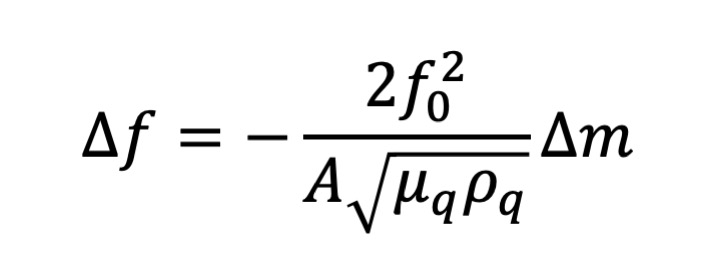ここで、Δ f は水晶振動子の振動数変化、Δ m は電極単位面積あたりに付着した物質の質量、
f 0 は水晶振動子の基本振動数、A は水晶振動子上の金属薄膜電極の面積、
μ q は水晶の男性率、ρ q は水晶の密度です。
この式は次のように導くことができます。水晶板の振動数は厚さが薄くなるほど高くなることが知られており、f 0 を
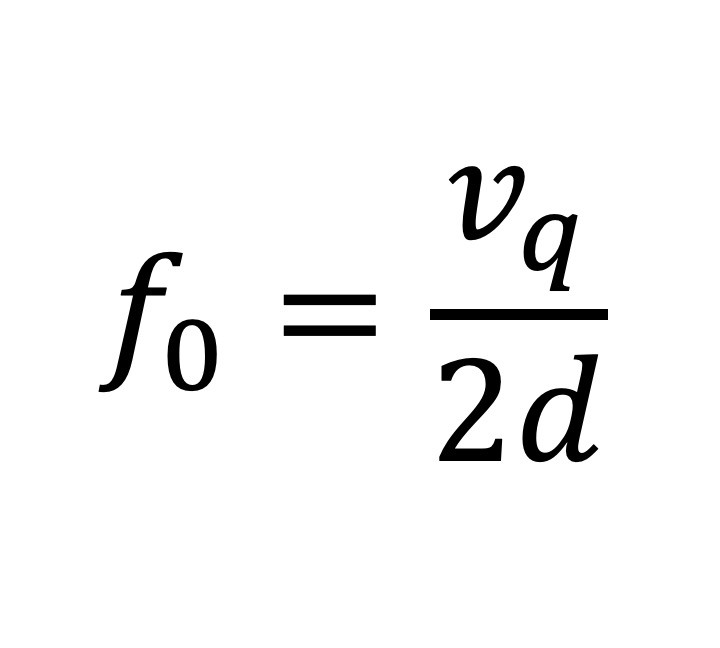と表します。ここで、vq はすべり振動の伝播速度であり、d は水晶板の厚さです (文献 [1]の式 (2))。
この式は、層の厚さ d が波長の半分であることを表しています。これは基本振動数の場合であり、より波長が短い倍音の場合には
分母の 2 が 2n (n は自然数) となります。
厚さ d が d + Δ d と変化したとき、振動数の変化は
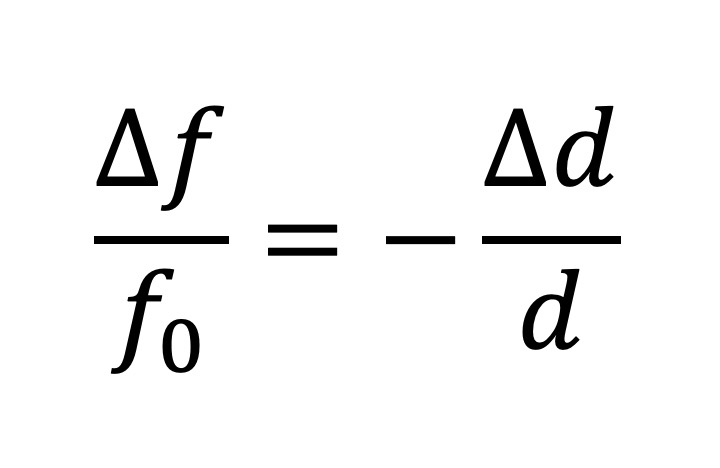となります。文献 [1] の式 (4) です。質量の変化は、Δ d と電極の面積 A に比例しますので
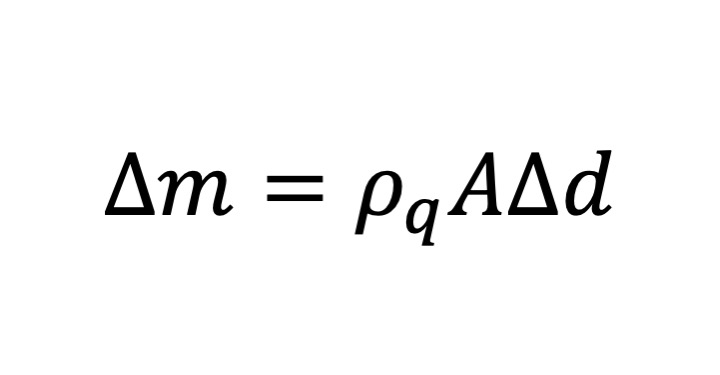とおきます。文献 [1] 式 (1) から得られます。すると振動数の変化は次のようになります。
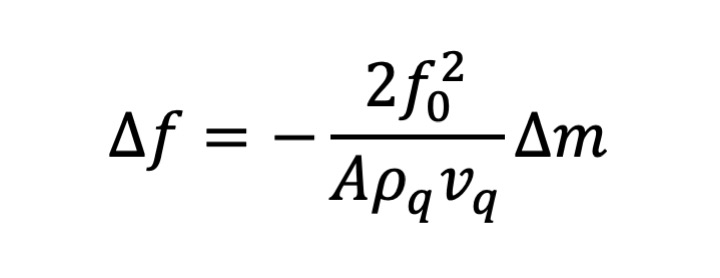伝播速度は vq = (μ q / ρ q)1/2と表わすことができますので
最初の振動数変化の式が得られます。
文献
[1] G. Sauerbrey: Zeitschrift fur Physik 155, 206-222 (1959).
Sauerbreyの論文はドイツ語であり読みにくいため、全文を日本語に翻訳しました。
Zeitschrift fur Physik はすでに廃刊になった雑誌ではありますが、書作権の問題があるかもしれませんので、
全文ではなく一部を参考のため下に載せます。
* * * * * * * * * * * * * * * * * * * *
薄層の計量とミクロ測定のための水晶振動子の使用
Gunter Sauerbrey
(1959年2月21日受理）
厚さが振動する水晶板に異物の層が付着すると、振動する質量が増加する結果として水晶板の固有振動数が変化する。
振動する水晶の振動数は正確に測定できるので、薄層の重さを測定する非常に感度の高い方法が得られる。
付着層の質量の存在比と振動数の変化はお互いに比例する。比例定数は、水晶振動子の固有振動数から計算できるため、
水晶振動子で層を計量する際に経験的な校正を行う必要はない。
層の重さの測定の精度は主に水晶の固有振動数の温度依存性により決まり、1℃ の許容温度変動量は
約 ± 4⋅ 10-9 g⋅ cm-2である。
これは、密度が ρ = 1 g ⋅ cm-3 で平均の厚さが 0.4 Å の場合である。
この方法を質量の直接計量（マイクロ計量）にも使用した。10-10 g の精度を達成できる。
1. 課題
薄層に関するほぼ全ての研究においては、層の厚さまたはそれと同等のパラメーターを決定する必要がある。
薄層の厚さを測定する一つの方法に計量法がある。層の厚さ d は質量 m により次の式により与えられる:
d = m / (F ⋅ ρ). (1)
ここで、F は層の面積であり ρ は密度である。薄層の場合、層のキャリアーが粗いので正しい面積が不明なことが多く、
特に単層の場合には巨視的な密度を考えることが重要になる。
計量により、層の平均質量は肉眼で見える表面の cm2 あたりの質量により測定できる。MayerとBehrndt1は、
高真空装置で溶融し高温で加熱した石英ガラス製の微量天秤により、単原子層を比較的高い精度での計量に初めて成功した。
高い測定精度が可能であり安定して一般的に使える計量方法を探索するために、現在は別の方法が取られている。
高周波で使われる厚さ剪断型（AT及びBTカット）の振動水晶板は、固有振動数が層の厚さだけでなく表面の異質層の厚さにも依存するため、
薄層の計量に適していることが示されている。
定性的にはこれらの依存性は以前から知られていた。水晶のターゲット周波数と金属電極の厚さを一致させることにより、
振動水晶の製造に使われた2。本研究において、薄層の計量に適した水晶振動子の方法を明らかにするために、
厚さ滑り振動の固有振動数に対する異質層の影響を調べる。
2. 異物層が存在する層の固有振動数
図1の水晶板の厚さ剪断（すべり）振動は横波の定在波である。基本振動モードでは、層の厚さは波長の半分に等しい。
固有振動数は次で与えられる:
f = vtr / (2d) = N / d. (2)
ここで、vtr は層の厚さ方向の弾性横波の伝播速度、d は層の厚さ、
N = vtr / 2は周波数定数を表す。
伝播速度 vtr すなわち水晶の振動について文献にある定数 N は水晶の結晶学的方向
すなわち水晶板の交差角度に依存する。固有振動数の温度係数がゼロである2つの厚さ剪断断面の場合、N
の値は次のようになる(Heising3):
AT-剪断: N = 1670 kHz mm
NT-剪断: N = 2500 kHz mm.
|
| |
| |
