|
|
| |

近藤効果と物理学
伝導電子が局在スピンと相互作用をすると、電気抵抗、比熱、帯磁率などいろいろな物理量に特異性が現われます。
これらの特異な現象は近藤効果と呼ばれています。
金属の電気抵抗にも異常が現れます。通常、電気抵抗は温度を下げると減少します。これは、電気抵抗の原因である原子の熱振動が
温度が下がると共に緩やかになり、熱振動による電子の散乱が弱くなるからです。電気抵抗の原因としては、ほかに不純物原子に
よる伝導電子の散乱があります。鉄やマンガンなどの原子が不純物として金属中にあると電気抵抗は増大し、原子の熱振動による
電気抵抗とを合わせて全体の電気抵抗は、温度が下がると共に減少していたものが逆に増大するという現象が起こります。
これは、1930年代に発見されたもので、抵抗極小現象と言われています(図1参照)。
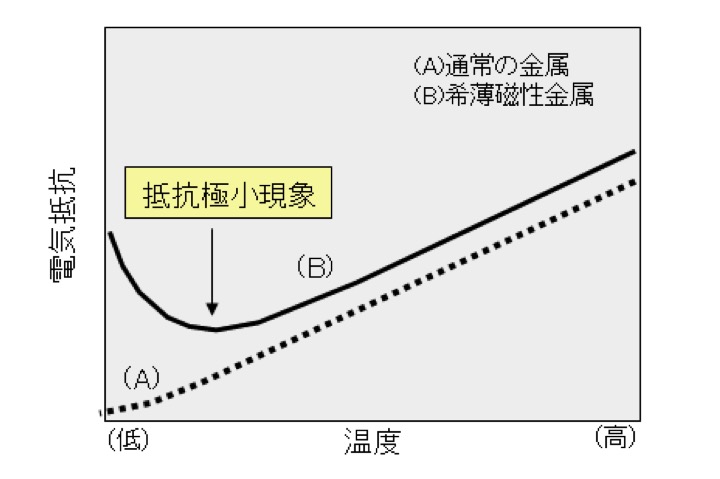
図1. 抵抗極小現象。
抵抗極小の機構の解明は、超伝導と並ぶ個体物理学における謎となっていました。抵抗極小の問題は当時の大問題であり、多くの物理学者によって研究されました。
電総研の近藤淳博士は、抵抗極小は局在スピンと伝導電子との相互作用の結果として起こることを示しました。
不純物原子がスピンを持つということが重要です。
不純物スピンは、絶えずその向きを変えています。温度が高い時は、電子の動きが速いので不純物スピンは止まって見えるために、電気抵抗は温度に依らなくなります。
温度が低くなりますと、電子の動きが遅くなり電子からは不純物スピンが絶えず向きを変えているのが見えるようになります(図2)。
この時は、電気抵抗は温度に依存し、驚くことに温度が下がると共に増大します。
これはすなわち抵抗極小現象であり、近藤理論により最初に示されました。
近藤理論によると、電気抵抗は対数的に、すなわちlogTのように増大します(図3)。
近藤理論以前には、不純物スピンが止まって見える場合の計算がなされていましたが、近藤理論においては不純物スピンが向きを変える効果を取り入れて、
電気抵抗の増大を説明しました。不純物スピンと伝導電子との相互作用による抵抗極小及び関連する現象を近藤効果と言います。
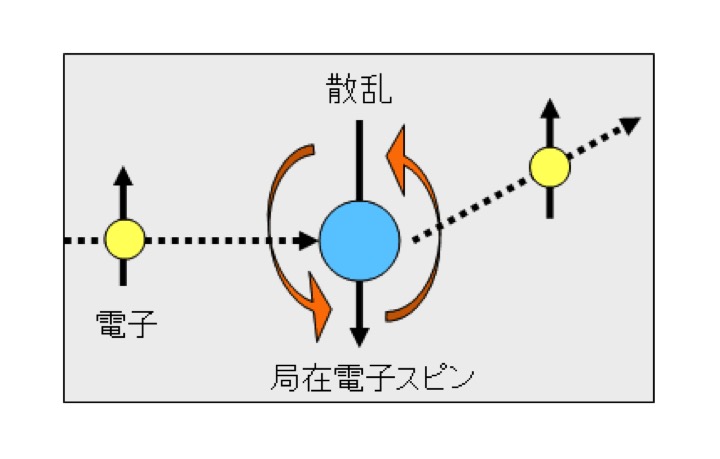
図2. 局在スピンによる電子の散乱。
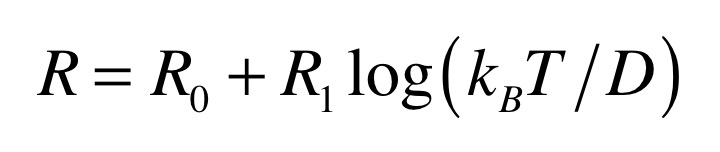
図3. 近藤効果の式。
電気抵抗が増大することがそれほど驚くようなことであるのかは、物理に馴染みがないとわかりにくいことです。
実際、20世紀のはじめ頃には、電気抵抗は低温ではどのように振る舞うのかわからず、実際に超低温環境を実現させて調べてみようというところから、
低温物理学が始まったわけです。
近藤効果の前に、まず電気抵抗についてわかっておかないといけない点が、近藤効果の説明を難しくしています。超伝導も同様ではありますが。
近藤理論により電気抵抗は温度が下がるとともに増大することが示さましたが、絶対零度ではどうなるかは、問題として残されました。
電気抵抗は対数的に増大しますので、絶対零度では発散してしまうわけです。
これがその後10年以上にもわたって物理学者を悩ませた近藤問題です。近藤問題が多くの研究者により研究されることにより、
近藤効果が普遍的な現象であることが明らかになりました。
特に、くりこみ群の方法により、くりこみ群を特徴づける方程式(ベータ関数と呼ばれている)が求められ、強結合固定点が存在することが明らかにされました。
(伝導電子の散乱により現われる対数発散は、くりこみ可能性を示唆していました。そのため、多くの研究者がくりこみ群の方法を近藤問題に応用しようとしました。)
すなわち、近藤効果の本質は、弱結合から強結合へのクロスオーバーにあり、クロスオーバーに伴う特異性として対数補正が現れたわけです。
近藤効果における、くりこみ群の流れ図は下の図のようになります。
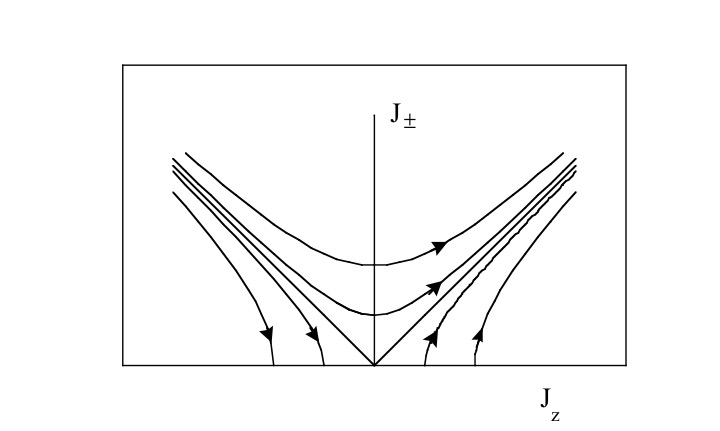
図4. 近藤モデルにおけるくりこみ群の流れ図。
局在スピンと伝導電子との交換相互作用が反強磁性(Jz > 0)の場合、Jが大きい強結合領域に繰り込まれて行きます。
この時、強い反強磁性相互作用により、局在スピンと伝導電子はスピンについて一重項状態を形成します。
強磁性(Jz < 0)の場合には、J⊥< |Jz|なら、J⊥
は0に繰り込まれていきます。
くりこみ群方程式は摂動論により求められたものですが、この描像が正しいことはK. G. Wilsonによる数値的くりこみ群の方法により確かめられました。
絶対零度においてスピン一重項が形成されることは、芳田奎博士により最初に指摘されました。
芳田博士は高温での摂動展開から、スピン一重項の形成を予想されましたが、後に正しいことがわかりました。卓見であったと言うべきでしょう。
このくりこみ群の流れ図は、Kosterlitz-Thouless (KT) transitionにおいて求められた流れ図と同じものです。
くりこみ群の方程式が同じであるからです。なお、くりこみ群の方程式が求められたのは、近藤効果の方が先でした。
このことより、近藤効果とKT転移は同じユニバーサルクラスに属すると言えます。
近藤モデル(s-dモデル)から、対数的なクーロン力で相互作用する電子ガスモデルの有効作用を導くことができます。
また、この電子ガスモデルから、サイン-ゴルドンモデルを導くことができます。近藤モデルと多くのモデルが密接に関連しており、
一つのユニバーサルクラスを形成しています。
(個人的には、Kosterlitz、Thouless、Kondoの三人でノーベル賞をもらうのが良いのではないかと思っていましたが、
残念ながらかないませんでした。)
また、近藤効果においては、低温すなわち低エネルギー領域において相互作用が強くなり、高温すなわち高エネルギー領域において相互作用が弱く なります。このような性質を漸近自由性と言います。局在スピンと伝導電子との相互作用は漸近自由性を持っているわけです。
漸近自由性はQCD(量子色力学)でよく知られています。クォークは、近距離(すなわち高エネルギー領域)では自由な粒子のように振る舞い、
離れようとすると(低エネルギー領域)強い力が働きます。
クォークの閉じ込めは、近藤効果におけるスピン一重項の形成に対応します。
近藤効果とQCDとは類似した現象であり、強いアナロジーがあります。くりこみ群の方程式の比較を下に示します。
漸近自由性を示すモデルとしては、他に非線形シグマモデルなどがあります。
非線形シグマモデルをより一般のリー群に拡張するとカイラルモデルと呼ばれているものになります。これに位相項を加えますとWess-Zumino-Wittenモデルとなります。
また、N=2超対称ゲージ理論も漸近自由性を示し、非くりこみ定理から高次項が消えるため低次のくりこみ群の方程式が正しい式となります。

図5. 近藤モデルとQCDのくりこみ群方程式。
このように、近藤効果は物理学のほとんどの分野に関連する非常にユニバーサルな現象であると言えます。
|
| |
| |

