観測される磁気異常は個々の磁性体のもたらす磁気異常のベクトル和(全磁力の場合はスカラー扱い)である。
モデリングを行う際には、欲しい構造の規模を考えて、うまく磁気異常を分離することが、大事。
モデリングを行う際には、欲しい構造の規模を考えて、うまく磁気異常を分離することが、大事。
磁気異常のイメージ:調査区域に置いて一次傾向面で近似される長波長成分と
局所的な構造によってもたらされる磁気異常の和。
よって局所的な構造異常を抽出するためには一次傾向面を除去する必要がある。
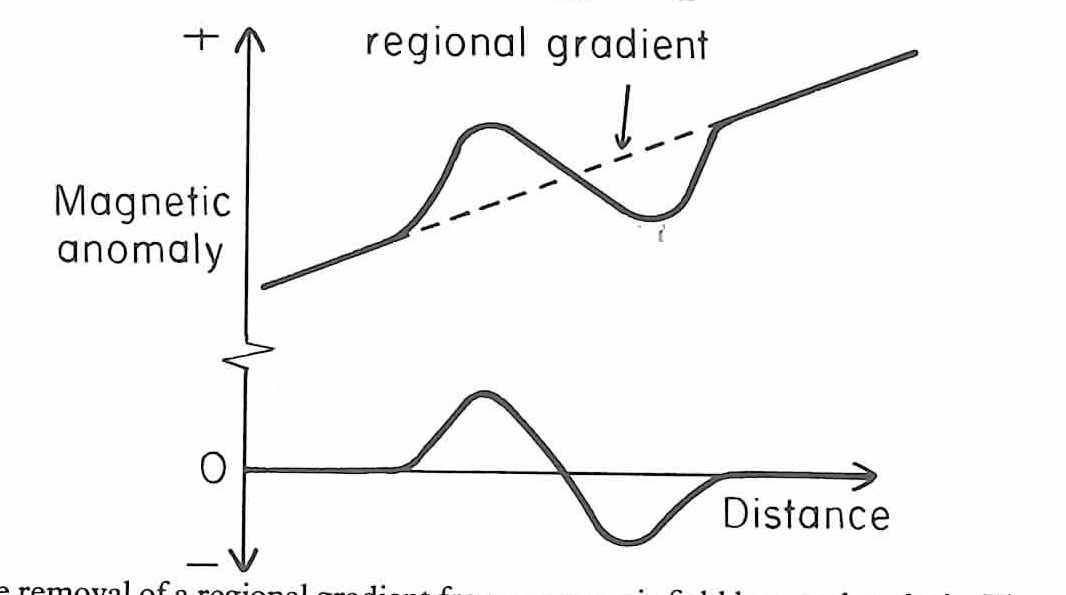
Kearey and Brooks(1984)より
よって局所的な構造異常を抽出するためには一次傾向面を除去する必要がある。

Kearey and Brooks(1984)より
- 一次傾向面は最小二乗法で求めてしまうのが簡単。出来合いのソフトウェアを使うと楽。エクセルの例も探せば出てくる
- カレイダグラフの例(私が使っているからということ以上の理由はないです)
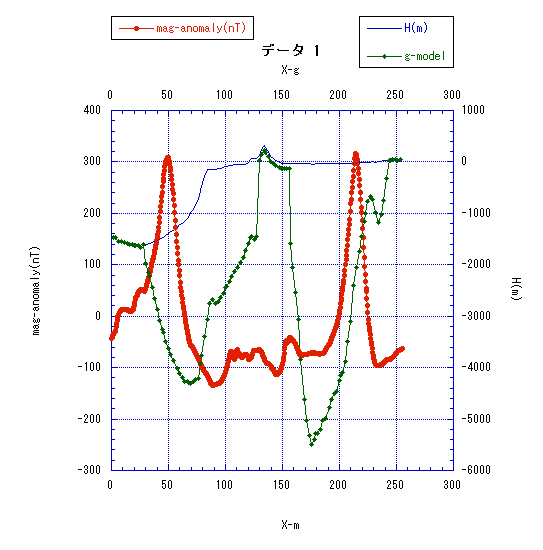
茶色の丸のデータを線形近似すると赤い式のようになる。
茶色の丸のデータから赤い式で計算される値を引いたのが青い四角のデータ。
- 平面の場合はGMTも使える → 例
- 倉庫の中にはPDF
- パワースペクトルを使って大まかな深度を推定し、上方接続フィルターで分離
- パワースペクトルを使って大まかな深度を推定する
- 一定の広がりのある区域内に多くの磁性体が存在するとき、それらの平均的な上面深度を推定するのにスペクトル解析を用いることが多い。
具体的には、
一次傾向面を取り除いた後に、二重フーリエ変換を計算し、
横軸に周波数、縦軸にパワースペクトルの自然対数をとったグラフを描き、
その傾きから複数の深度を求める。
- 浦川の例
パワースペクトルをm=nの場合について計算した。
計算方法はこちら
ここではA、B、Cの3本の直線が引ける。
直線の傾きからAは約3.7km、Bは約1km、Cは約0.5kmと推定される。
これは観測面からの値であるから、このデータでは飛行高度が約450mなので実際の深度はこれより0.45km浅い。
ゆえにAは約3.3km、Bは約0.5km、Cは約0.0km、となる。
ここでは地表に超塩基性岩体が露出しているので妥当な値と考える。
一般的にはAは長周期成分、Bが求めたい構造、Cはノイズ成分、という判断をする。
- 一定の広がりのある区域内に多くの磁性体が存在するとき、それらの平均的な上面深度を推定するのにスペクトル解析を用いることが多い。
- 上方接続フィルターを使って分離する
- 上記のパワースペクトルを用いた成分分離を参考にして、直線Aの成分を除く。
上方接続を使って3-4km上空で観測される磁気異常を計算し、観測磁気異常から除去する。
- 浦川のデータを用いて具体的な例を示す
実際の計算方法はこちら
- 元の観測データから3kmの上方接続データを引いた残り。
残差データ(25nTコンター)

- 上記のパワースペクトルを用いた成分分離を参考にして、直線Aの成分を除く。
- パワースペクトルを使って大まかな深度を推定する
- 二層モデル(磁性体の上面深度の起伏が磁気異常を作ると仮定した場合)→堆積盆の解釈など(物理探査ハンドブックp513)
構造境界を推定する場合、一様磁化が大前提
- フォワードモデル
- 磁性体の縁と上面深度を決める。
大事なのはピークを合わせるようにすること。
細かいことは気にしないこと。
- 磁化の方向は外部磁場と平行から始めるのが無難。
- 磁化強度は地質学的な裏付けから大体の値を採用する
- 磁化強度の目安
誘導磁化:J=κH κ:体積磁化率(SIならば無次元),H:外部磁場強度
- 測定値が無い時の目安の例
- Physical Properties of Rocks, G.Angenheister ed., Springer-Verlag, 1982より
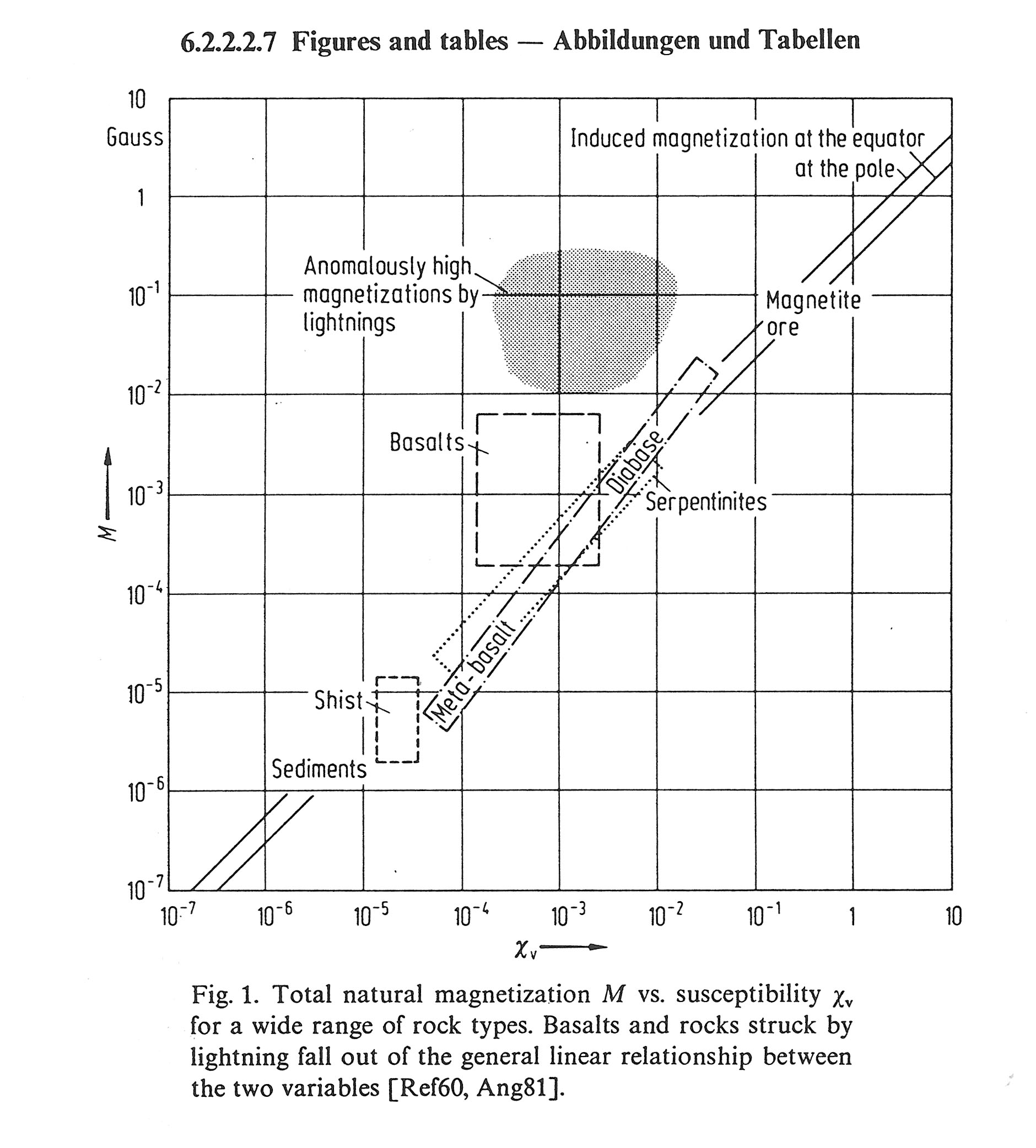
- Rock Physics and Phase Relations -A Handbook of Physical Contents, T.J.Ahrens ed., AGU, 1995より
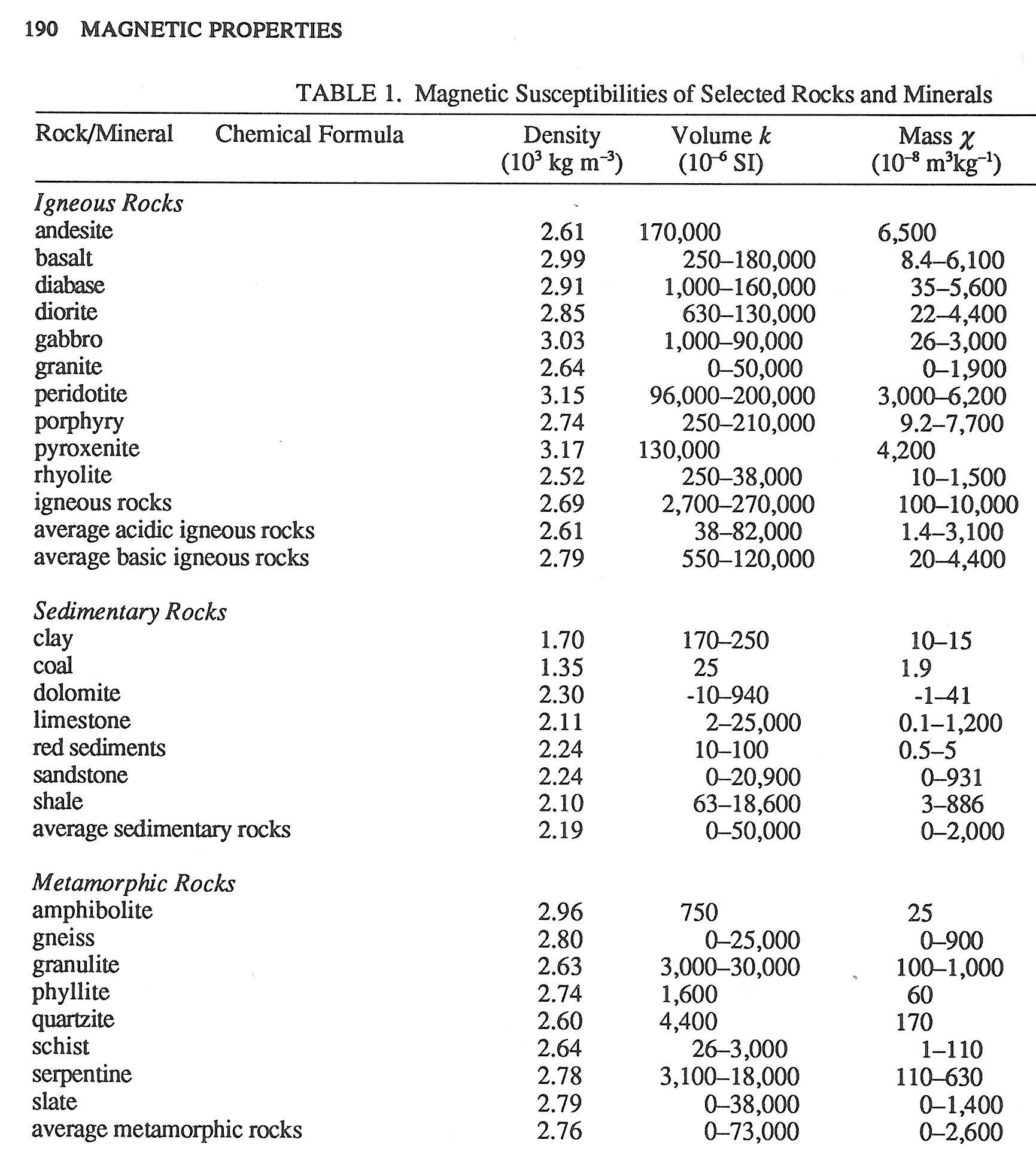
- Physical Properties of Rocks, G.Angenheister ed., Springer-Verlag, 1982より
- 具体例
磁化率を5.0×10-2SIとすると,誘導磁化は磁化率の平均値とIGRFの全磁力値(日本付近では約46000 nT)の掛け算になる。
0.05×46000nT=5×46×10-8(T)=23×10-7(T)
T(テスラ)はB(磁束密度)の単位で、A/mはH(磁場)とJ(磁化)の単位。よってH=B/μ0。
μ0=4π×10-7H/m、T=Wbm-2、H=WbA-1より1T={1/(4π×10-7)}A/m。ゆえに、23/(4π)=1.83A/mと計算される。
上の目安の例を見ると、5.0×10-2SI程度の磁化率の岩石は、だいたい10-3G=1A/m程度の自然残留磁化を持つことが多い。
よってこのような例では、磁場の計算には、両方を足して、2-3A/mくらいを与えることが多い。
- 磁化強度の目安
- 磁性体の縁と上面深度を決める。
- インバースモデル
- 非線形方程式を解くことになるので、いろいろ技術的な工夫が多くなされている。
安定に解をもとめる計算技法はどんどん新しいものが出ているので、論文等をフォローしてください。
中塚正さんによる研究公開資料
No518(2009)、 No519(2009)
(磁気異常データの処理から解析に至るまで多くのプログラムのソースコードが公開されている)
- ここでは昔教わったごーくごく基本のことがらのみ書いています。
- 磁性体の深さを推定する古典的な方法(高緯度で適用)
- Maximum Depth
外部磁場の成分をr=(rx,ry,rz)としたら
磁気異常の最大値をAmax、一次微分をA'=dA(x)/dx、二次微分をA"=d2A(x)/dx2とする。
最大深度dは8(rx2+rz2)1/2×(Amax/A')より浅くなる。
そしてd2は9.42(rx2+rz2)1/2×(Amax/A")より浅くなる。
- 2次元の磁気異常のテストデータとして、外部磁場を伏角90°偏角0°、磁化を伏角90°偏角0°、磁化強度5A/m、厚さ10kmとしたときに深さ1kmと5kmの場合の磁気異常を計算した。
X=15kmから20kmのところに磁性体がある。
磁気異常の最大値は深さ1kmの場合x=17.5のとき1933.6、深さ5kmの場合x=17.5のとき597.0、
ここで一次微分を取るとその最大値は、深さ1kmの場合x=14.5kmの点で875.52、深さ5kmの場合x=14.0kmの点で100.875。
二次微分を取るとその最大値は、深さ1kmの場合x=14.0kmの点で559.95、深さ5kmの場合x=11.0kmの点で17.168。
今、rの項を1とすると
Mmax/A'maxはそれぞれ1kmの時が2.2、5kmの時が5.9となる。
よって最大深度は8×2.2=17.6kmと8×5.9=47.2kmとなる。
さらにMmax/A"maxはそれぞれ1kmの時が3.45、5kmの時が34.77となる。
よって最大深度は√(9.42×3.45)=5.7kmと√(9.42×34.77)=18.1kmとなる。
二次微分が取れればこちらのほうがうまくあてはまりそうである。
- Maximum Depth
- オーソドックスな解き方
磁化強度と上面深度は、磁気異常の性質を考えると、同時に解けない。必ずどちらか一方を与えること。
インバージョンについての解説はたとえば斎藤正徳(2011)。
- 磁性体の深さを推定する古典的な方法(高緯度で適用)
- できれば単独は避ける(特にインバースモデルの場合)
- 磁気異常は構造や磁化強度の変化に敏感である。
重力のインバージョンでは2層モデルの重力差を0.3g/cm3、0.4g/cm3、0.5g/cm3の3種類で計算しても構造モデルの大筋は変わらないが、 磁気異常のインバージョンでは磁化強度差を0.1A/m、0.5A/m、1.0A/mの3種類で計算するとモデルが大きく変わるという例。
- 完全に埋没していて、他にデータが無い場合はやむを得ないが、地質分布や地震波、重力異常などから得られる構造を参照し、それをコントロールポイントとして構造モデルを修正して行く方が無難な場合が多い。
- サンプルデータについて重力異常から2層モデルを計算してみる
- 重力データから求めた基盤の起伏に磁化強度分布を載せるやり方もある。
- 磁気異常は構造や磁化強度の変化に敏感である。
- 非線形方程式を解くことになるので、いろいろ技術的な工夫が多くなされている。
- 磁化強度分布→火山体の解釈など(物理探査ハンドブックp514)
磁性体の形を仮定して、磁気異常分布をうまく説明できるように磁化強度分布に置き換えたもの
⇒火山地域の解析によく用いられる
磁化方位は外部磁場と平行と仮定されることが多い
- 3次元モデル
Nakatsuka(1995)以降は共役勾配法(CG法)の適用が常識化しているらしい。
3D-imagingとして、高分解能で得られた磁気異常データに対応した解が得られるよう、いろいろ新しい計算技術が開発されている。
- 3次元モデル
- フォワードモデル
- 擬(似)重力・極磁力
- フーリエ解析を実行するにあたっての注意事項(地球システムのデータ解析.萩原・糸田(2001)より)
- どんなデータでも吟味することなくフーリエ解析にかける人がいるが、それは周期性を知らない人のすることである。フーリエ解析の前提には、データの両端点の値が等しい、すなわちf(0)=f(N)という重要な関係が暗に含まれていることを留意しなければならない。例えばf(N-1)とf(0)の値の間に著しい差がないように、データの前処理を施す必要がある。
- データに直線的トレンドが見られる場合には、まず最小二乗法によってデータからトレンドを取り除いたあとに、はじめてフーリエ解析を実行するほうが良い。
- どんなデータでも吟味することなくフーリエ解析にかける人がいるが、それは周期性を知らない人のすることである。フーリエ解析の前提には、データの両端点の値が等しい、すなわちf(0)=f(N)という重要な関係が暗に含まれていることを留意しなければならない。例えばf(N-1)とf(0)の値の間に著しい差がないように、データの前処理を施す必要がある。
- フーリエ解析を実行するにあたっての注意事項(地球システムのデータ解析.萩原・糸田(2001)より)
ポテンシャル論から導かれる関係
- 擬(似)重力とは、磁化強度を密度に置き換えた時に期待される重力異常に相当する。
- 具体的には全磁力異常を外部磁場方向に積分し、さらにそれを磁化方向に積分する。
- 最後にこれを鉛直方向に微分する。
- 密度と磁化強度の比は100kg/m3(0.1g/cm3)が1A/mに相当すると考えられている(Blakely,1995)。
- 極磁力は擬(似)重力を鉛直方向に微分したもので、磁化物体の磁化方向と外部磁場方向がともに鉛直下方を向いているときに得られると期待される磁気異常に相当する。
- しかしながら、通常、磁化物体の磁化方位はわかっていないので便宜上外部磁場方位と平行と仮定して計算されるからなかなか理想通りには行かない。
- 駒澤正夫氏による検証
合わせ技の例
- 日本海東縁部の3か所について
1.重力異常から基盤深度を計算
2.重力基盤深度を磁性体上面と仮定して磁化強度分布を計算
森尻(1999)
- 根室・釧路地域の重磁力異常から推定される中規模地質構造
1.高重力異常を説明するには基盤層の起伏だけではなく地下浅部に基盤層よりも密度の高い貫入岩体の存在を考える必要がある。
2.根室層群中の一部に貫入・噴出相として産出するアルカリかんらん石粗粒玄武岩を採取して、密度・自然残留磁化強度・磁化率のほかいくつかの磁気パラメーターの測定を行った。
3.プロファイルを2本取り,高重磁力異常帯を説明するような2次元構造モデルを計算した。モデルのパラメーターは粗粒玄武岩の測定値を参照して与えた。
4.釧路沖で2列見られる高磁気異常は、釧路根室にかかるところは粗粒玄武岩によるもの、帯広沖に見られるものは蛇紋岩によるものと推察される。
森尻・中川(2014)
※モデル計算に使われていない岩石磁気パラメーターは、報告には含まれていないが、交流消磁・熱消磁・ARM着磁実験も行っている。古地磁気・岩石磁気データまとめ
海山の構造の推定
研究例はいろいろある
- たとえば
Toshiya Fujiwara, Yukari Kido, Yoshihiko Tamura, Osamu Ishizuka, Gravity and magnetic constraints on the crustal structure and evolution of the Horeki seamount in the Izu-Ogasawara (Bonin) arc, Earth Planets Space, 61, 3, 333-343, 2009.
- 古い有名なところでは
Victor Vacquier and Seiya Uyeda,Palaeomagnetism of Nine Seamounts in the Western Pacific and of Three Volcanoes in Japan.東京大学地震研究所彙報. 第45冊第3号, 815-848, 1967.
- 自分でやった簡単な例(フォワードモデル)では
こちら(2007年大水深報告書から)
海洋底の拡大の研究など
やったことないのでよくわからないが研究例はたくさんある
- たとえば
Kyoko Okino, Yasuhiko Ohara, Toshiya Fujiwara, Sang-Mook Lee, Kin'ichiro Koizumi, Yasuyuki Nakamura, Shiguo Wu, Tectonics of the southern tip of the Parece Vela Basin, Philippine Sea Plate, Tectonophysics, 466, '3/4, 213-228, 2009.
- 超有名なのはこれ
F. J. VINE and D. H. MATTHEWS, Magnetic Anomalies Over Oceanic Ridges. Nature 199, 947-949 (7 September 1963)
| Quantity | SI | cgs | SI×f→cgs | cgs×f→SI |
|---|---|---|---|---|
| Magnetic induction(B) | T | G | 1[T]=1[Wbm2]×104→G | 1[T]=1[G]×10-4→[T]=100[μT] |
| Magnetic field(H) | A/m | Oe | 1[A/m]×(4π/103)→[Oe] | 1[Oe]×(103/4π)→[A/m] |
| Magnetic moment | Am2 | emu | 1[Am2]×103→[emu] | 1[emu]×10-3→[Am2] |
| Volume magnetization | A/m | emu/cc | 1[A/m]×10-3→[emu/cc] | 1[emu/cc]×103→[A/m] |
| Mass magnetization | Am2/kg | emu/g | 1[Am2/kg]×1→[emu/g] | 1[emu/g]×1→[Am2/kg] |
| Bulk susceptibility | m3 | emu/Oe | 1[m3]×(106/4π)→[emu/Oe] | 1[emu/Oe]×(4π/106)→[m3] |
| Volume susceptibility | SI | G/Oe | 1[SI]×(1/4π)→[G/Oe] | 1[G/Oe]×(4π)→[SI] |
| Mass susceptibility | m3/kg | emu/(Oe・g) | 1[m3/kg]×(103/4π)→[emu/Oe・g] | 1[emu/Oe・g]×(4π/103)→[m3/kg] |
- メモ
cgsからSI単位系への移動をスムースに行うために、SI慣用系という単位が導入された。
磁場の単位としてT、磁化の単位としてA/m、が推奨された。
- 磁場はB:B=μ0(H+J)
もともと磁場HはcgsでOeだから磁束密度BのcgsでのGaussとは違う次元である。
それを慣用系では一緒にした。
- 1nT=1γ=10-5G
- 磁化はJ:磁気モーメントM(1emu=Gcm3)から単位体積当たりの磁化は、1A/m=10-3emu/ccに読みかえる。
- μ0=4π×10-7H/m
- Wb=kgm2A-1s-2 T=Wbm-2=kgA-1s-2 H=WbA-1=kgm2A-2s-2
- mass magnetization[emu/g]×density[g/cc]=volume magnetization[emu/cc]
- mass susceptibility[emu/g/Oe]××density[g/cc]×4π=volume susceptibility[G/Oe]×4π=volume susceptibility=volume susceptibility[SI]