

 次へ: 後方散乱の消失とベリーの位相
上へ: 不純物散乱
戻る: 不純物散乱
次へ: 後方散乱の消失とベリーの位相
上へ: 不純物散乱
戻る: 不純物散乱
2次元グラファイトに任意のポテンシャルがある場合を考えよう.
強束縛模型から出発し有効質量方程式(
1)を導くのと同様にして有効ポテンシャル
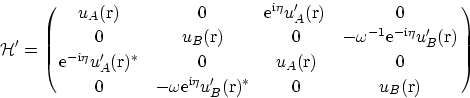 |
(6) |
を導くことができる.[
15]
ここで
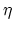
は
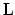
と
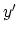
軸(図2)のなすカイラル角であり,
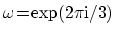
である.
各行列要素は任意のポテンシャルについて一般的に定義される量であり, 定義は文献[
15]にあるが, 大雑把に言って, 対角要素は強束縛模型の格子点のポテンシャルを格子定数の数倍程度の範囲で疎視化したものであり, 非対角要素は
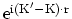
とポテンシャルの積を同様に疎視化したものである.
対角項はK点付近の状態の間の散乱あるいはK'点付近の状態の間の散乱である谷内散乱を表す.
一方, 非対角項はK点からK'点あるいはK'点からK点への散乱である谷間散乱を表す.
しばらく, 簡単のためポテンシャルの到達距離 が十分小さいときに限定し, 各行列要素の表式を示して議論する.
ナノチューブを特徴付ける長さスケールとして, 格子定数
が十分小さいときに限定し, 各行列要素の表式を示して議論する.
ナノチューブを特徴付ける長さスケールとして, 格子定数 やポテンシャルの到達距離
やポテンシャルの到達距離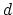 の他にも軸方向の波長
の他にも軸方向の波長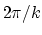 , 円周
, 円周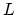 , 磁気長
, 磁気長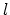 等があげられる.
ポテンシャル到達距離が十分小さいとは,
等があげられる.
ポテンシャル到達距離が十分小さいとは,
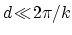 ,
, 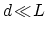 ,
, 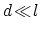 の場合である.
この場合,
の場合である.
この場合,
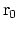 を不純物ポテンシャルの位置として
を不純物ポテンシャルの位置として
とデルタ関数で置き換えることができる.
ここで, 強束縛模型を採用すれば
であり,
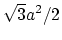
は単位格子の面積,
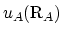
と
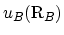
は各々格子点
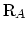
と
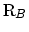
のポテンシャルを表す.
また,
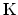
と
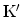
はKとK'点での波数である.
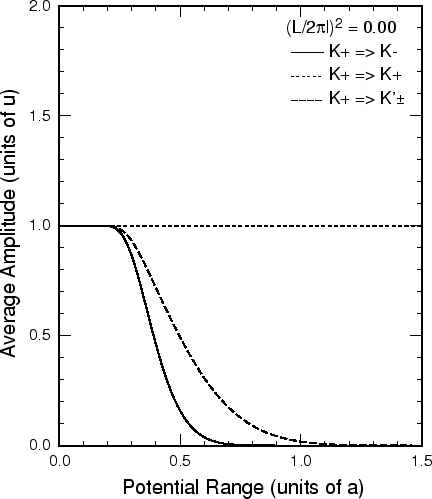
図3:
磁場がないときの散乱行列要素.
実線は谷内の後方散乱, 点線は谷内の前方散乱, 破線は谷間の散乱を示し,
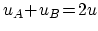 である.
後方散乱はポテンシャル到達距離が格子定数より大きいとき指数関数的に減少する.
である.
後方散乱はポテンシャル到達距離が格子定数より大きいとき指数関数的に減少する.
 |
ポテンシャル到達距離が格子定数に比べて大きいとき
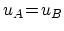
となり,
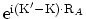
と
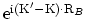
が激しく振動する為, 有効ポテンシャルの非対角要素
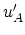
と
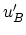
は無視できる.
これは, KとK'の間の谷間散乱が無視できることを意味している.
 で, 波動関数 (5) 式を使うとポテンシャル(6) 式の行列要素は
で, 波動関数 (5) 式を使うとポテンシャル(6) 式の行列要素は
となる.
ここで, 添字
と
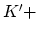
は正の群速度,
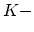
と
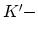
は負の群速度を持つ状態を表す.
磁場がないとき谷内の後方散乱
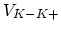
と
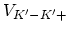
は
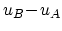
に比例し, 到達距離が格子定数程度と極端に短いポテンシャルの場合を除けば, 最低次のボルン近似の範囲で, 散乱体があっても後方散乱が消滅することを示している.
一例としてBサイトに中心を持つ, 半値幅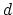 のガウス型ポテンシャルを考える.
図3にポテンシャル到達距離
のガウス型ポテンシャルを考える.
図3にポテンシャル到達距離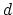 の関数として散乱強度を示した.
後方散乱確率は
の関数として散乱強度を示した.
後方散乱確率は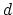 の増加と共に急速に減少し,
の増加と共に急速に減少し, 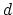 が格子定数を越える場合には指数関数的に小さくなる.
一方ナノチューブの軸に垂直に磁場をかけた場合は, (5)式から明らかなように谷内散乱が長距離ポテンシャルについても残る.
が格子定数を越える場合には指数関数的に小さくなる.
一方ナノチューブの軸に垂直に磁場をかけた場合は, (5)式から明らかなように谷内散乱が長距離ポテンシャルについても残る.
図4:
磁場をかけたときの電気伝導率.
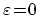 のとき, さまざまなポテンシャル到達距離について有効質量近似の計算結果を示す.
のとき, さまざまなポテンシャル到達距離について有効質量近似の計算結果を示す.
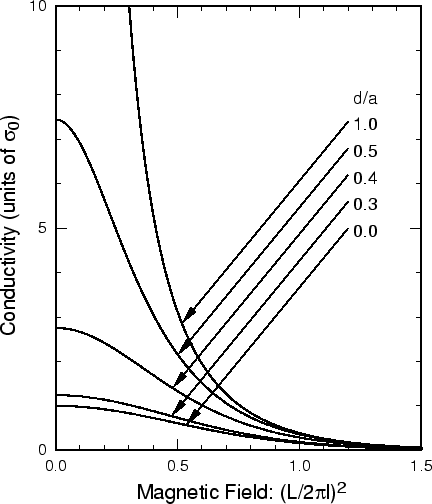 |
図4 に電気伝導率を磁場の関数として示す.
常に正の磁気抵抗効果がみられ, 特に零磁場において散乱が消失する場合にはそれが顕著になる.
![]() が十分小さいときに限定し, 各行列要素の表式を示して議論する.
ナノチューブを特徴付ける長さスケールとして, 格子定数
が十分小さいときに限定し, 各行列要素の表式を示して議論する.
ナノチューブを特徴付ける長さスケールとして, 格子定数![]() やポテンシャルの到達距離
やポテンシャルの到達距離![]() の他にも軸方向の波長
の他にも軸方向の波長![]() , 円周
, 円周![]() , 磁気長
, 磁気長![]() 等があげられる.
ポテンシャル到達距離が十分小さいとは,
等があげられる.
ポテンシャル到達距離が十分小さいとは,
![]() ,
, ![]() ,
, ![]() の場合である.
この場合,
の場合である.
この場合,
![]() を不純物ポテンシャルの位置として
を不純物ポテンシャルの位置として

![]() で, 波動関数 (5) 式を使うとポテンシャル(6) 式の行列要素は
で, 波動関数 (5) 式を使うとポテンシャル(6) 式の行列要素は
![]() のガウス型ポテンシャルを考える.
図3にポテンシャル到達距離
のガウス型ポテンシャルを考える.
図3にポテンシャル到達距離![]() の関数として散乱強度を示した.
後方散乱確率は
の関数として散乱強度を示した.
後方散乱確率は![]() の増加と共に急速に減少し,
の増加と共に急速に減少し, ![]() が格子定数を越える場合には指数関数的に小さくなる.
一方ナノチューブの軸に垂直に磁場をかけた場合は, (5)式から明らかなように谷内散乱が長距離ポテンシャルについても残る.
が格子定数を越える場合には指数関数的に小さくなる.
一方ナノチューブの軸に垂直に磁場をかけた場合は, (5)式から明らかなように谷内散乱が長距離ポテンシャルについても残る.


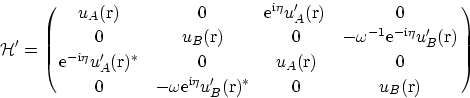
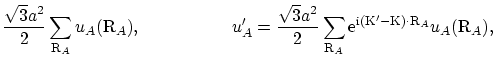
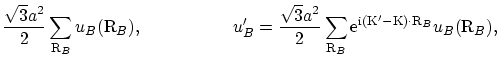
![$\displaystyle {1\over2A} [ \pm u_A F_-(x_0)^2 \!+\! u_B F_+(x_0)^2] ,$](img126.png)
![$\displaystyle {1\over2A} [ \pm u_A F_+(x_0)^2 \!+\! u_B F_-(x_0)^2] ,$](img128.png)
![$\displaystyle {1\over2A} [ \mp u'^*_A \!-\!\omega {{\rm e}}^{{{\rm i}}\eta} u'^*_B ] F_+(x_0) F_-(x_0) ,$](img130.png)
![$\displaystyle {1\over2A} [ \mp u'_A \!-\!\omega^{-1} {{\rm e}}^{-{{\rm i}}\eta} u'_B ] F_+(x_0) F_-(x_0) .$](img132.png)
