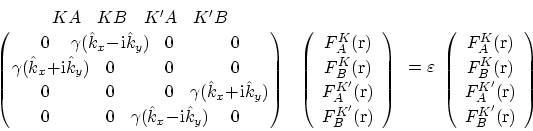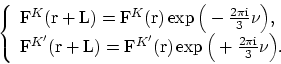金属的ナノチューブと半導体的ナノチューブ
ナノチューブは直径と螺旋構造により金属にも半導体にもなる. このことは蜂の巣格子の強束縛模型で等方的な最近接格子の遷移積分
2次元グラファイトのフェルミエネルギー付近のバンドは結合への寄与が弱い![]() 軌道からなり, 第一ブリルアン域の端にある K 点と K' 点付近で, 波数の一次に比例する分散を持つ.
グラファイトの電気的性質は, この K 点と K' 点付近の状態で決まる.
有効質量近似では, 電子の波動関数はブロッホ関数と有効質量方程式
軌道からなり, 第一ブリルアン域の端にある K 点と K' 点付近で, 波数の一次に比例する分散を持つ.
グラファイトの電気的性質は, この K 点と K' 点付近の状態で決まる.
有効質量近似では, 電子の波動関数はブロッホ関数と有効質量方程式
 |
を導入する. (1)式は, 質量0の電子に対するディラック方程式と, KまたはK'について2行2列の部分はニュートリノに対する2行2列の Weyl 方程式とそれぞれ形式的に同じである.[10]
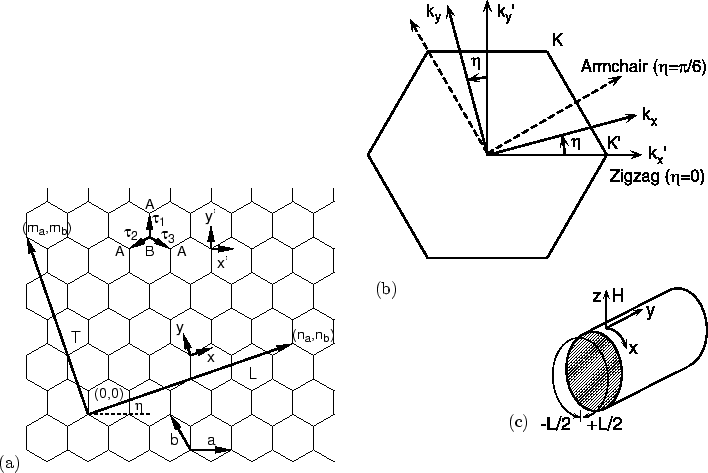
ナノチューブの構造は図 2 に示すように, グラファイトを丸めたときに重なる格子点をむすぶカイラルベクトル
![]() により決まる.
ここで,
により決まる.
ここで,
![]() と
と
![]() は2次元グラファイトの格子ベクトル,
は2次元グラファイトの格子ベクトル, ![]() と
と ![]() は整数である.
カイラルベクトルの向き
は整数である.
カイラルベクトルの向き![]() をカイラル角と呼ぶ.
実際,
をカイラル角と呼ぶ.
実際, ![]() と
と
![]() の場合を除けば, 一般にナノチューブは螺旋構造をもつ.
例外的な
の場合を除けば, 一般にナノチューブは螺旋構造をもつ.
例外的な![]() をジグザグ構造ナノチューブ, また
をジグザグ構造ナノチューブ, また
![]() を肘掛椅子構造ナノチューブとよぶ.
を肘掛椅子構造ナノチューブとよぶ.
直径の大きなナノチューブの場合, 円筒状に丸めることによる![]() と
と![]() 軌道の混ざりあいを無視でき,[7] ナノチューブの電子状態は円筒の周方向に周期境界条件を課すことにより得られる.
ブロッホ関数は, K点とK'点がブリルアン域の中心ではないために, 円周を一周したときに位相
軌道の混ざりあいを無視でき,[7] ナノチューブの電子状態は円筒の周方向に周期境界条件を課すことにより得られる.
ブロッホ関数は, K点とK'点がブリルアン域の中心ではないために, 円周を一周したときに位相
![]() がつく(
がつく(![]() がK点,
がK点, ![]() がK'点).
ただし
がK'点).
ただし ![]() は,
は, ![]() を整数として
を整数として
で定義される. 包絡関数に対する境界条件はその位相を打ち消すだけの余分の位相がつく. すなわち,
一般化周期境界条件(2)式のもとで有効質量方程式(1)を解くと, ナノチューブの電子のK点付近のエネルギーは
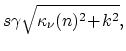 |
|||
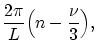 |
(3) |
で与えられる. ここで,