1. Publications list (in antichronological order)
  2. Abstracts (of publications by topics)
  3. Selected talks (with slides)
  4. Curriculum Vitae

Research Interests

Theoretical Study of Quantum Transports in Mesoscopic Systems

  1. Carbon Nanotubes


    1. Absence of back scatterings

      A carbon nanotube is an ideal conductor. We have shown absence of back scattering in metallic carbon nanotubes. Our purpose of the study was to answer a fundamental question; how conducting electrons are scattered in carbon nanotubes.

      For a start we usually consider impurity scatterings as an origin of the electrical resistance. Atoms of air, nano particles of graphite, and other dust on substrate are examples of the impurity, which interact electrostatistically with the conducting electrons. Most of the impurity has a potential range longer than the lattice constant of graphite. We call them "long-range potential". In normal metal, the conducting electrons are scattered in all directions by impurities. Is it the case of carbon nanotube? No! Carbon nanotubes are one dimensional and thus electrons are scattered either forward or backward direction. Surprisingly the backward scatterings are absence exactly in carbon nanotubes with the long-range potential, which means 0 resistance or perfect conduction.

      We explain the absence of back scatterings as an example of Berry's phase. It is also related to the fact that an effective Hamiltonian in the effective-mass scheme is the same with Weyl's equation of neutrino or mass-less Dirac Hamiltonian.

      In more detail, see Abstracts and Links to our paper

    2. Conductance with 2 STM probes

      In more detail, see abstract or PDF

    3. Aharonov-Bohm effects


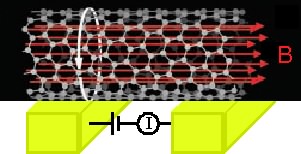
      In more detail, see Abstracts and Links to our paper

    4. A Point defect

      We have studied scatterings of the conduction electron by a short-range potential. A point defect is an example of the short-range potential. We have shown conductance quantization, which follows an interesting rule.

      In more detail, see Abstracts and Links to our paper

    5. Topological defects [Topological Defects] on carbon nanotubes
    6. A contact with dirty electrode [Contact]
    7. Crossed nanotubes [Crossed Carbon Nanotubes]
    8. Logic circuits with nanotube transistors have studied with experimentalists. [Application]

    For links to nanotube-related sites, go to the nanotube page.

  2. Fano effects in an Aharonov-Bohm ring with a quantum dot
    The quantum transport in an AB ring with a quantum dot has been studied. We have shown Fano effects in the calculated conductance and given an explanation for the recent experiment by Kobayashi et al. (PRL 88, 256806 (2002).

    In more detail, see Abstracts and Links to our paper

  3. Fermi-Edge Singularity in a Lateral Periodic Potential
    This work is a collaboration with experimentalists.

    In more detail, see Abstracts and Links to our paper

  4. Numerical Study of Quantum Transport Using Equation-of-Motion Method
    We have investigated weak-localization phenomena in two-dimensional systems in the presence of time-dependent potentials by solving numerically the time-dependent Schrödinger equation.

    In more detail, see Abstracts and Links to our paper

  5. Quantum Transport in Antidot Lattices
    We have explained AAS oscillations observed in the magneto resistance in antidot lattices by using recursive Green's function technique.

    In more detail, see Abstracts and Links to our paper

This page was last updated on: 8 Sep. 2023
Back to MathAM-OILMathAM-OIL | AISTAIST