磁場中の波動関数

次へ: 不純物散乱 上へ: ナノチューブの電子状態 戻る: 金属的ナノチューブと半導体的ナノチューブ

磁場中の波動関数

ナノチューブの軸と垂直に磁場

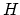
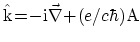
をかけたときは, 有効質量方程式(1)で, $\hat{\fam\mbfam\tenmb k}\!=\!-{{\rm i}}\vec\nabla\!+\!(e/c\hbar){\fam\mbfam\tenmb A}$ と置けばよい. ここで, ランダウゲージ

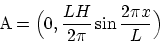$\begin{displaymath} {\fam\mbfam\tenmb A}=\Big(0,{LH \over 2\pi}\sin{2\pi x\over L}\Big) \end{displaymath}$

(4)

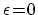
を用いると, 特に $\epsilon\!=\!0$ では解析的な取り扱いが可能であり, 波動関数は

$\displaystyle {\fam\mbfam\tenmb F}^K_{sk}$	$\textstyle =$	$\displaystyle {1\over\sqrt{2A}} \pmatrix{ - {{\rm i}}s (k/\vert k\vert) F_-(x) \cr F_+(x) \cr} \exp({{\rm i}}ky) ,$
$\displaystyle {\fam\mbfam\tenmb F}^{K'}_{sk}$	$\textstyle =$	$\displaystyle {1\over\sqrt{2A}} \pmatrix{ + {{\rm i}}s (k/\vert k\vert) F_+(x) \cr F_-(x) \cr} \exp({{\rm i}}ky) ,$	(5)

である.[14] ここで,

$\begin{displaymath} F_\pm(x) = {1 \over\sqrt{LI_0[2(L/2\pi l)^2]}} \exp \Big[ \pm \Big({L\over2\pi l}\Big)^2 \cos{2\pi x\over L} \Big] , \end{displaymath}$

であり,

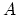
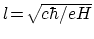
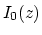
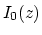
はナノチューブの長さ, 磁気長 $l\!=\!\sqrt{c\hbar/eH}$ , $I_{0}(z)$ は第１種の変形ベッセル関数である. $I_{0}(z)$ は

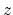
が小さいとき

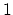
の程度であり,

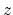
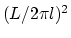
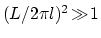
が大きくなると指数関数的に増大することに注意する. $(L/2\pi l)^2$ は磁場に比例したパラメーターであり, ナノチューブの半径と磁気長の比の２乗である. 強磁場( $(L/2\pi l)^2\!\gg\!1$ )では

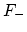
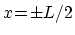
は円筒の下部 $x\!=\!\pm L/2$ のまわりに局在し,

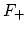
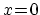
は上部 $x\!=\!0$ に局在する. その局在長は

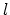
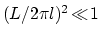
の程度である. 一方, 弱磁場( $(L/2\pi l)^2\!\ll\!1$ )では, 波動関数が円周方向に広がっている.

また波動関数(5) に対応する群速度は

$\begin{displaymath} v={\gamma \over \hbar I_0[2(L/2\pi l)^2]}{sk \over \vert k\vert} \end{displaymath}$

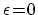
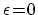
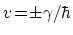
である. $\epsilon\!=\!0$ は4重に縮退しているのが, 輸送現象を考えるために, ナノチューブに入射する状態と出ていく状態を分離したことになっている. 磁場がないとき, $\epsilon\!=\!0$ 付近で正負の群速度 $v\!=\!\pm\gamma/\hbar$ をもつ状態がK点とK'点に一組づつあり, 強磁場では群速度の大きさは指数関数的に減少し, それに対応し状態密度が指数関数的に増加する.