後方散乱の消失とベリーの位相
実は磁場が無い場合, 任意のポテンシャルがあっても非対角成分がゼロで対角成分が等しい場合には後方散乱が完全に消失することが示せる.[15] 例えばK点に対する有効質量方程式(1)はパウリ行列と書ける. 磁場がない場合, 波動関数は
で与えられる. ここで
で与えられる.
ポテンシャルの到達距離が格子定数よりも大きい場合には,
![]() と
と
![]() は無視できるので, 谷内の後方散乱を考える.
また
は無視できるので, 谷内の後方散乱を考える.
また
![]() であり, そのフーリエ変換を
であり, そのフーリエ変換を
![]() とする.
後方散乱
とする.
後方散乱
![]() の
の![]() 行列の
行列の![]() 次の項は,
次の項は,
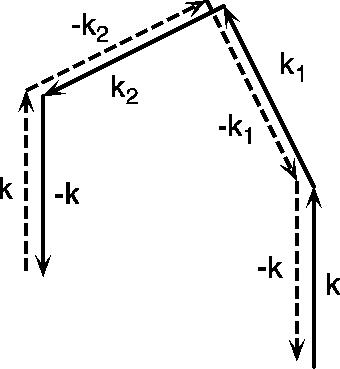
となる. 図5は
により得られる項が存在し, それは図5に点線で示したように時間反転した電子の運動に対応する. 両方の行列要素についてポテンシャルのフーリエ変換とエネルギー分母は不変であるが, スピン部分は同じ大きさの逆符号となることを示せる.[16] それは, スピン回転の演算子が
以上の議論から明らかなように, それぞれの散乱過程がスピンの回転と対応づけて記述される. これは, Weyl方程式で記述されるニュートリノがヘリシティー, すなわちスピンがいつも波数ベクトルの方向を向いているという性質を持っている為である. しかしながら, 2次元グラファイトのフェルミ準位近傍の電子状態は形式的にWeyl方程式で記述されるが, 波動関数の二つの要素は実際の電子スピンを表しているのではなく, ただ単位セル中の二つのカーボン原子の波動関数に対応しているだけであることに注意する.
スピン空間の![]() 回転が波動関数の符号の変化を与えることを見てきたが, 波数空間の原点回りの回転も同じ符号の変化を与え, それはベリーの位相の一例として直接得られる.[17]
次のような波動関数を考えよう.
回転が波動関数の符号の変化を与えることを見てきたが, 波数空間の原点回りの回転も同じ符号の変化を与え, それはベリーの位相の一例として直接得られる.[17]
次のような波動関数を考えよう.
| (13) |
これは, スピン軌道相互作用が強い系では, 量子干渉効果により後方散乱過程が減少し, 電気伝導率が増加する効果と類似している.[19] スピン軌道相互作用がないとき, 各々の散乱過程は, それと時間反転した過程とおなじ散乱強度を与え, その干渉効果によって後方散乱確率が増加する. これが弱局在の理論における量子補正である.[20] 一方スピン軌道相互作用が存在する場合は, 不純物散乱はスピンの回転を伴うので, 波動関数の位相を反転し, 同様の干渉効果は後方散乱確率を減少させる.[21] 2次元グラファイトでは, 波数空間の原点での縮退した特殊な分散関係のために, ベリーの位相をとおしてこの反局在効果が最も極端に現れた例と見なすことができる.


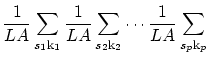
![$\displaystyle {V(-{\fam\mbfam\tenmb k}\!-\!{\fam\mbfam\tenmb k}_p) \cdots V({\f...
...bfam\tenmb k}_2)] [\varepsilon\!-\!\varepsilon_{s_1}({\fam\mbfam\tenmb k}_1)] }$](img162.png)