短距離ポテンシャルと格子欠陥

次へ: 電気伝導の実験 上へ: 不純物散乱 戻る: 後方散乱の消失とベリーの位相

短距離ポテンシャルと格子欠陥

バンド幅を超えるようなポテンシャルを少数の原子サイトに置いた模型を議論する.[22] これは, 短距離ポテンシャルの極端な場合である. この模型の計算には格子模型のリカージョン法を用いた.[23,24] この手法を用いると, 格子模型を仮定したあとは全く近似なしに透過係数 $t_{mn}$ , 反射係数 $r_{mn}$ が数値的に計算される. ここで, 添字の

は入射する波を示し

は出ていく波を示す. $\epsilon\!=\!0$ では $\{m,n\}$ として $\{K,K\}$ , $\{K,K'\}$ , $\{K',K\}$ , $\{K',K'\}$ の4組がある. コンダクタンスはランダウアー公式[25]を用い, 電子スピンの自由度による２倍も含めて

$\begin{displaymath} G={e^2\over\pi\hbar}\sum_{m,n}\vert t_{mn}\vert^2, \end{displaymath}$

で与えられる.

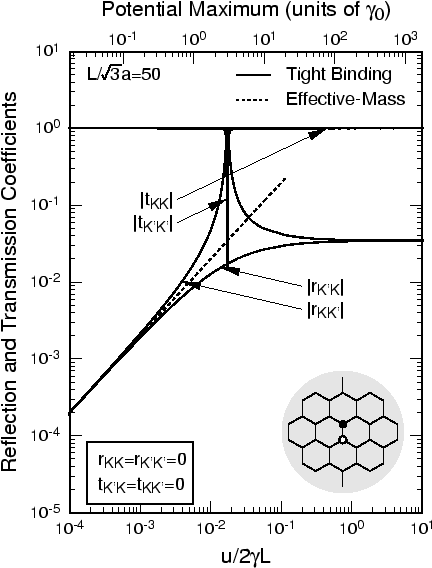
図3に例示したように, 短距離ポテンシャルの場合, 電子は後方散乱される. 短距離ポテンシャルの極限は, 一つまたは数個の格子点にのみポテンシャルを置いた場合である.

**図 6:** 透過係数 $t_{m,n}$ と反射係数 $r_{m,n}$ の大きさ. 挿入図の黒丸(Aサイト)と白丸(Bサイト)で示した格子点にのみ散乱ポテンシャルがあり, 横軸はその強さである. 添字のKとK'はK点とK'点を意味し, KKとK'K'は谷内の, KK'とK'Kは谷間の散乱を表す. 点線は行列要素(9)式を示す.
$\begin{figure}\epsfxsize =100mm {\hfill \epsfbox{825q.eps}\hfill} \end{figure}$

図6に2つの格子点にポテンシャルを置いたときの透過反射係数をポテンシャルの高さの関数として示す. 反射係数はポテンシャルの高さがバンド幅の半分 ( $3\gamma_0$ ) になったとき共鳴的に大きくなる. さらに, ポテンシャルが増加すると, 反射確率は減少し無限大のポテンシャルがあっても, ほとんど透過する.

実際, 無限大のポテンシャルもしくは実際に格子点を取り除いたときの同様の計算によると $\epsilon\!=\!0$ のコンダクタンスは奇妙なルールに従って量子化される.[22] すなわち, 取り除いたA, B副格子の格子点数を, として, $\vert N_A\!-\!N_B\vert\!=\!0$ の場合図6に示したようにほとんど完全透過であり, 僅かな反射確率はナノチューブの円周の2乗に反比例して減少する. $\vert N_A\!-\!N_B\vert\!=\!1$ のとき半分反射して半分透過となりコンダクタンスは量子化コンダクタンス $e^2/\pi\hbar$ になる. $\vert N_A\!-\!N_B\vert\!\ge\!2$ では完全反射となる. コンダクタンスはそれぞれ大きなエネルギー依存性を示すが, 各一次元バンド端ではいずれの場合も完全透過に対応し, $2e^2/\pi\hbar$ となる.

さて実際に散乱ポテンシャルとして何が考えられ, そのポテンシャル到達距離はどの程度だろうか? ナノチューブは作製過程において金属微粒子やナノ粒子と呼ばれる炭素分子が付着している. また, 層間物質など金属微粒子を意図的に導入することもできる. これらのクーロン力による散乱ポテンシャルは格子間隔に比べて十分長いと予想される. 一方, 格子欠陥等により原子サイトが欠落したような構造も考えられる. 格子欠陥の周りで実際にはバンドや原子間隔がひずむ効果などを考えなければならないが, それらを無視して波動関数が0になることを取り入れ最も単純化した模型が今議論した数個の格子点を取り除いた模型である.