次へ: おわりに 上へ: jmssj4 戻る: カーボンナノチューブ接合系

朝永-Luttinger流体

以上の議論では, 電子間相互作用は無視できる場合を取り扱った. 電子間相互作用のある一次元電子系は朝永-Luttinger流体の方法で, 分散曲線をFermi面近傍で線形化する近似の後, ボゾン化の手法でその他の近似のない解が得られる. 金属的ナノチューブのFermi面付近の分散は直線であり, 朝永-Luttinger流体のほぼ理想的な系である. ただし, 有効的なクーロン相互作用の大きさとサブバンド間エネルギーギャップがともに直径の逆数でスケールされる疑一次元系であることや,[55] Fermi点がKとK'点に2個あることについては, 注意深く考察しなければならない. トンネル伝導度についての理論は,電子間相互作用が重要となる場合トンネル確率が抑制されることを示している.[56]-[59] 大雑把に言うと多体の波動関数は協調してトンネルしなければならずトンネル確率が減少するのである. 理論によると, トンネル伝導度

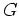
は温度

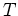
, 電圧

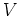
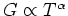
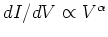
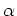
の関数として, $G\propto T^\alpha$ , $dI/dV\propto V^\alpha$ である. $\alpha$ と相互作用パラメーター

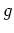
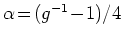
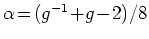
の関係は, トンネル接合の種類によって異なるが, 例えば, 図2 (a)の終端接合の場合 $\alpha\!=\!(g^{-1}\!-\!1)/4$ , (b)側面接合の場合 $\alpha\!=\!(g^{-1}\!+\!g\!-\!2)/8$ の関係がある. ここで,

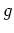
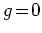
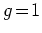
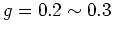
は斥力的な相互作用の場合, 強相関極限 $g\!=\!0$ から, 相互作用のないとき $g\!=\!1$ の間の値を取る. 実験的に色々なトンネル接合を用いて, トンネル伝導度が測られた.[43],[60]-[62] 最初の実験は電極とナノチューブの接触抵抗が巨大なため, そこにトンネル障壁がある場合であり, これは終端接合に相当する.[60] その後, トンネル障壁をより明確にするため上述のナノチューブ接合系[61],交差したナノチューブ[43]およびAFMで人工的に折り曲げたナノチューブ[62]で, トンネル伝導度の温度や電圧依存性が測定され, 全ての場合にほぼ $g=0.2\sim0.3$ が得られた.