次へ: 朝永-Luttinger流体 上へ: jmssj4 戻る: 交差したナノチューブの電気伝導

カーボンナノチューブ接合系

**図 4:** ナノチューブ接合系の模式図. 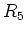で示した位置に一つの5員環, 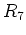で示した位置に一つの7員環を持ち, 太い方のナノチューブの周長が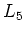, 細い方が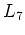である.
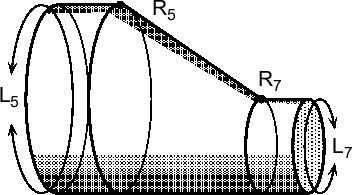$\begin{figure} \epsfxsize =80mm {\hfill \epsfbox{cn1jcins.eps}\hfill} \end{figure}$

ナノチューブ接合系とは異なる円周のナノチューブが連続的につながった系である. このような構造を持つ系は, アーク放電等によるナノチューブの生成時に混在する. 図4の黒丸で示した位置に, 一つの5員環(R

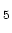
)と7員環(R

)が配置したと考えると, ダングリングボンドや大きな格子定数のひずみを導入せずに円周やカイラリティの違うナノチューブを連続的につなぐ構造を取れる. 一組の5員環と7員環の組は蜂の巣格子中の

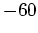
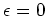
度の回位となる. したがって, この種の欠陥は, 多角形欠陥, トポロジカルな欠陥と呼ばれる.[48] この欠陥はナノチューブに独特な欠陥といえる. トポロジカルな欠陥は不純物欠陥と違ってその効果がスカラーポテンシャルとして表せないが, 電子散乱の原因になり得る. この系の輸送現象についての最初の理論的取り組みとして, 接合部のトンネル伝導度の計算がある.[49] また, 金属-半導体-金属接合を考えるとトンネル電流が流れるのでナノスケールのデバイスとしての可能性が提案されている.[50] 格子模型にランダウアー公式を用いた数値計算や有効質量近似を用いた計算により, 伝導度は接合の詳細にほとんどよらないことが明らかになった.[51],[52] Fermiレベル( $\epsilon=0$ )の伝導度は両端のナノチューブの円周の比

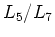
だけにより決まりナノチューブのカイラル角や円周の長さ自身には依らない. ここで,

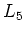
は太いナノチューブの円周,

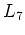
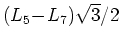
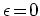
は細いナノチューブの円周であり, 接合部の長さは $(L_5\!-\!L_7)\sqrt{3}/2$ である. 有効質量近似で長さのスケールを考えると, $\epsilon\!=\!0$ でFermi波長が無限大であるため, この接合系の場合は

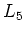
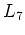
の2つしか存在しないので, $\epsilon\!=\!0$ での伝導度が円周の比でスケールされるのは自然である. また十分長い, つまり円周の比が小さい接合系では伝導度は接合の長さの3乗に反比例して減少する. しかしながら, ナノチューブの軸に垂直に磁場をかけるともう一つの長さの単位として磁気長が加わるので, 少し複雑になる. ナノチューブの軸に垂直な磁場をかけた場合について, ランダウアー公式を用いた数値計算によると短い接合の場合は正の磁気抵抗が, 長い接合の場合は負の磁気抵抗が現れる.[53] しかしいずれの場合も, 伝導度の大きさは磁場の5員環7員環方向の成分だけの関数で決まる. 一方, 最近の有効質量近似による計算は接合系のコンダクタンスが磁場によってほとんど変化しないことを示している.[54] この違いの原因は不明である.