トップ| 略歴| 研究内容| 論文| 論文妙録| 解説| 講演|

抵抗のない導線

最初に電気伝導の最も簡単な問題として, 単層ナノチューブ上の散乱ポテンシャルによる電子散乱を有効質量近似で取り扱う.[18],[19] 理論の詳細は比較的詳しい解説が文献[11], [12]にあるので, ここでは結果だけ簡単に紹介する. 有効質量近似では, 電子の波動関数はブロッホ関数と有効質量方程式

$$\begin{array}{c}\begin{array}{cccc} KA & KB & K'A & K'B \end{arra... ...t{k}_x\!-\!{{\rm i}}\hat{k}_y) \!\!\!\!\!\! & 0 \end{array} \right) \end{array}$$

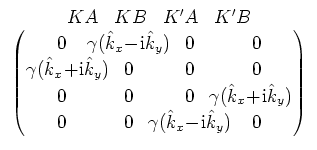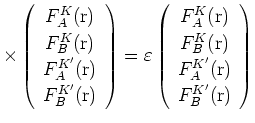$$\times \left( \begin{array}{c}F_A^K ({\fam\mbfam\tenmb r}) \\ F_... ...} ({\fam\mbfam\tenmb r}) \\ F_B^{K'} ({\fam\mbfam\tenmb r}) \end{array}\right)$$ (1)

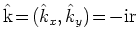
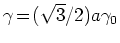
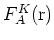
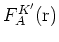
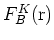
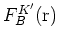
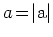
に従う包絡関数の積で与えられる.[5] ここで, $\hat{\fam\mbfam\tenmb k}\!=\!(\hat k_x,\hat k_y)\!=\!-{{\rm i}}\hbox{\cmbsy\char''72}$ は波数演算子, $\gamma\!=\!(\sqrt3/2)a\gamma_0$はバンドパラメーターであり, $F_A^K ({\fam\mbfam\tenmb r})$, $F_A^{K'} ({\fam\mbfam\tenmb r})$ と $F_B^K ({\fam\mbfam\tenmb r})$, $F_B^{K'} ({\fam\mbfam\tenmb r})$ はそれぞれAとB副格子の包絡関数であり, 格子定数 $a\!=\!\vert{\fam\mbfam\tenmb a}\vert$ のスケールでゆっくり変化する. ここで, 2次元グラファイトの単位格子は2個の炭素原子からなり, それらを図 1 (a)に示すようにAとBとする. (1)式は, 質量0の電子に対するディラック方程式と, KまたはK'について2行2列の部分はニュートリノに対する2行2列の Weyl 方程式とそれぞれ形式的に同じである. 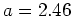まず最初に, 散乱ポテンシャルが格子定数($a=2.46$)の範囲ではゆっくり変化するような長距離型ポテンシャルを考える. 有効ポテンシャルは対角行列となりその成分は全て等しい. ここで後方散乱確率をボルン近似の範囲で計算すると0になる. これは次のように理解できる. Fermi面で交差する２つの分散直線はそれぞれ左向きと右向きに動く電子に対応する. 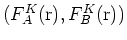その波動関数は分子の結合状態と反結合状態に対応しており, 隣り合う原子のスケールでこれらの波動関数すなわち $(F_A^K ({\fam\mbfam\tenmb r}), F_B^K ({\fam\mbfam\tenmb r}) )$は直交している. このとき対角型の有効ポテンシャルにより電子の運動方向を変えることはできない. さらに散乱のT行列を無限次まで計算しても, 後方散乱確率は厳密に0となる. 上述のボルン近似はその最低次に相当する. そこでは, 波数空間での多重散乱に対応する一つの項と, それと時間反転対称な項がうち消しあっている. これはニュートリノに似ている. ニュートリノのスピンは常にその運動方向を向いている. 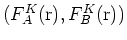この２成分の波動関数 $(F_A^K ({\fam\mbfam\tenmb r}), F_B^K ({\fam\mbfam\tenmb r}) )$を疑スピンとみなすと, ナノチューブ上の電子も同じ有効方程式1 に従うので, 当然同じ性質を持つ. この波動関数を波数空間の原点の周りで反時計回りにゆっくり一周すると, ベリーの位相を付けなければならない.[20] なぜなら原点はエネルギー縮退があるため幾何学的特異点となっているからである. 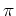ベリーの位相はちょうど$\pi$であり, これが上述の打ち消し合いを言い換えたことになっている. ところでナノチューブの軸に垂直な磁場をかけると, 不純物散乱が生じ正の磁気抵抗が期待される.[18] 最近, 後方散乱に関する単層ナノチューブを用いた実験が幾つか報告されている.[21]-[23] 初期の実験では低温で接触抵抗が巨大なためクーロン振動を示した. 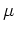一つの傍証として, その共鳴ピークが温度を下げると高くなり量子化伝導度の程度に近づく.[21] このとき平均自由行程はナノチューブの長さ8$\mu$mとなる.[22] より直接的には, 両端に電極を付けたナノチューブの上に置いたAFMチップを電圧端子として用いた実験が報告されている.[23] 単層ナノチューブではナノチューブの軸に沿って電圧降下がないが, 多層ナノチューブではほぼ一様にある. 一方, 多層ナノチューブでは量子化伝導度を報告した一つの例外[24]を除いて, 弱局在やAAS振動が報告されている.[25] これは, 不純物散乱があることを意味しており, 多層ナノチューブに上記の理論を適応できないようである. 単層ナノチューブと多層ナノチューブの違いについてはっきりした結論には到達していないが, 実験では電極または化学的ドーピングによりFermi準位が中性のものからずれ, 比較的太くサブバンド間隔の狭い多層ナノチューブは一次元的でなくなっている可能性, 面間の相互作用について[26],格子欠陥や格子ひずみの大小など色々議論がある. また, 軸平行方向の磁場での振動がバンドギャップに対するAharonov-Bohm効果で説明できるとの報告もある.[27]

著者のホームページ