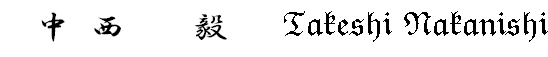トップ| 略歴| 研究内容| 論文| 論文妙録| 解説| 講演|

格子欠陥と量子化伝導度

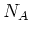
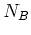
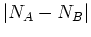
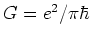
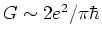
次に短距離型ポテンシャル, 例えば格子欠陥を考えよう. このときの有効ポテンシャルにはK点からK'点へ散乱する要素つまり有効ポテンシャルの非対角項があり, また一般にA, Bサイトで等しくない. ナノチューブの一箇所に欠陥を作り, それは$N_A$個のAサイトと$N_B$個のBサイトからなる場合を考える. 伝導度を, 格子モデルを用いた数値計算と有効質量の方法により調べた結果, 特異な量子化規則を見いだした.[28],[29] Fermiレベルでの伝導度$G$は差$\vert N_A-N_B\vert$だけに依存し, 差が2以上の場合完全反射, 差が１の場合半分透過 $G=e^2/\pi\hbar$,差が0の場合ほぼ完全透過 $G\sim 2e^2/\pi\hbar$となる. また, Fermiエネルギーを変えると伝導度は増加し次のサブバンド端のエネルギーで必ず完全透過になる. このとき欠陥の有効ポテンシャルは繰り込まれて0になるのである. 短距離ポテンシャルに関連し, 窒素やボロンで炭素を置換しドーピングした場合が, 第一原理計算により調べられており, 似た結果が予言されている.[30] さらにナノチューブの軸に垂直に磁場をかけると, 伝導度の磁場依存性は複雑であるが, おおむね正の磁気抵抗を示す.[31] 最近磁場がないときのFermiエネルギー依存性に関する実験が報告された.[32],[33] ナノチューブは, 化学気相成長法で作成された. これは今までのところ比較的格子欠陥を導入しやすいとされるサンプル作成法である. 格子欠陥をトンネル障壁とするドットのために, クーロン振動が観測されるが, あるゲート電圧では, クーロン振動が消滅する.[32] このとき格子欠陥によるトンネル障壁の有効ポテンシャルが小さくなり消滅したと考えられる.[28],[29] クーロン振動が観測されない別の実験では, ゲート電圧が小さいとき電気伝導度は小さくゲート電圧の関数として激しく振動し, 局在効果を示す.[33] ところが, ゲート電圧が大きくなると振動しながら量子化伝導度に近付く. 振動は２種類あり, 細かい振動はナノチューブの一電子レベル間隔から, 大きな振動は干渉効果から説明できる.

著者のホームページ