次へ: 金属的ナノチューブと半導体的ナノチューブ
上へ: jmssj4
戻る: jmssj4
カーボンナノチューブは新種の量子細線である.
飯島澄男先生による発見[
1]以来その電気伝導特性が理論的, 実験的に調べられカーボンナノチューブは大変特異な伝導特性を持つことが分かってきた.
また, 新しいナノスケールデバイスの材料となる可能性も議論されている.
そこで本稿では最近の電気伝導に関する研究を概説する.
まず第一にナノチューブの特徴はそのサイズにある.
円筒の直径はおおむね7から300 であり, 長さは1
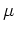
m以上になる.
半導体へテロ構造などで人工的に作られ, 従来提案され研究が進められてきた量子細線やデバイスよりずっと細長い.
二次元グラファイト面を円筒状に丸めてナノチューブを作ると, 円周方向の波数が量子化され, 量子化された一次元バンドの間隔は円周に反比例し, 直径
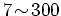
のナノチューブに対して
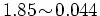
eVである.
これは, 室温よりも大きなエネルギー間隔であり, 電子の運動がナノチューブの軸方向だけに制限され, 一次元量子細線と見なすことができる.
また従来の量子細線が人工的な閉じこめポテンシャルによって電子が細線に閉じこめられるのに対し, ナノチューブでは周期境界条件により閉じこめられているので, 細線境界の乱れがなく, 比較的綺麗な量子細線といえる.
本稿では, 次にあげる興味深いナノチューブの電気伝導特性を概説する.
ナノチューブの電子状態は非常に特殊であり, グラファイト面の巻き方の違いにより金属的であったり半導体的であったりする.
最も興味深い理論的予言は後方散乱の消失である.
格子定数のスケールよりゆっくり変化する不純物ポテンシャルがあっても, 電子の後方散乱がないので抵抗のない理想的な導線となる.
一方格子欠陥は後方散乱の原因となりうるが, その場合も特異な量子化伝導度の規則がある.
電極とナノチューブの接合は重要な問題である.
Schottky障壁のポテンシャルが対数関数で表され系全体のオーダーの長さになるような非常に長いものとなり, これは全く新しいデバイスデザインを必要とすると共に, 新しい可能性がある.
ダイオードなどデバイスの応用も数々提案されている.
単純な交差したナノチューブや, 少数の5,7員環を含み異なる直径のナノチューブをつないだ構造を持つ接合系は, 電子状態の違うナノチューブをつないだ構造を提供する.
金属的ナノチューブではFermi面で交差する直線の分散関係が特徴である.
したがって一次元で重要となる電子間相互作用を考えるとき朝永-Luttinger流体の方法に可能性がある.
実際, 朝永-Luttinger流体としてトンネル伝導度の理解が進んでいる.
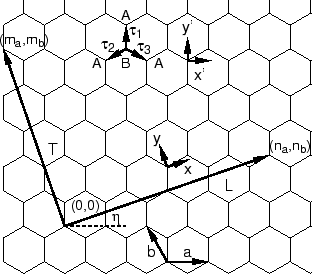
図 1:
(a) 2次元グラファイトの蜂の巣格子.
円周を与えるベクトル
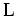の始点と終点が重なるように丸めることによりナノチューブが作られる.
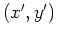はグラファイト面に固定した座標系であり, 
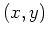は
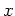軸が
に平行になるようにとる.
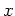軸と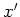
軸のなす角をカイラル角とよび
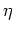であらわす.
特に,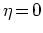 
をジグザグ構造ナノチューブ,
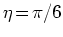を肘掛椅子構造ナノチューブとよぶ.
 |
