次へ: 不純物散乱 上へ: jmssj4 戻る: はじめに

金属的ナノチューブと半導体的ナノチューブ

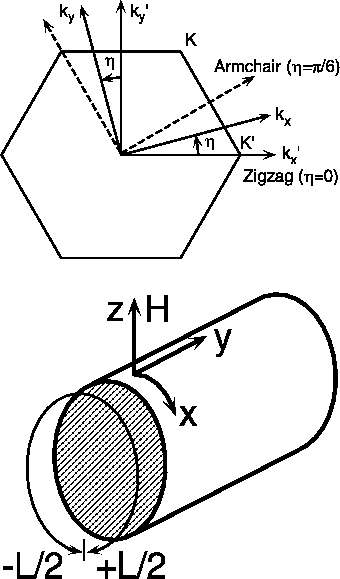
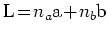
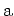
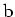
ナノチューブの構造は図 1 (a)に示すように, グラファイトを丸めたときに重なる格子点をむすぶカイラルベクトル ${\fam\mbfam\tenmb L}\!=\!n_a{\fam\mbfam\tenmb a}\!+\!n_b{\fam\mbfam\tenmb b}$ により決まる. ここで, ${\fam\mbfam\tenmb a}$ と ${\fam\mbfam\tenmb b}$ は２次元グラファイトの格子ベクトル,

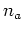
と

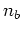
は整数である.

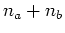
が3の倍数の時Fermi面で交差する直線の分散関係をもち金属的であり, それ以外は半導体的である. つまりグラファイト面の巻き方の違いにより3分の1は金属的, 3分の2は半導体的となる.

**図 1:** (b) グラファイト面の第一ブリルアン域. $\pi$ バンドはK点とK'点でFermiエネルギーを横切る.
**図 1:** (c) ナノチューブの円周方向に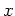軸, 軸方向に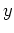軸をとる. 磁場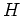は軸に垂直にかける.
$\begin{figure} \epsfxsize =80mm \epsfbox{bz2dg97a.eps} \setcounter{figure}{0} \epsfxsize =80mm \epsfbox{cnstr97a.eps} \end{figure}$

この変化は非常に激しく, カイラルベクトルを, 格子ベクトル変化させるだけで, 金属からeV程度のバンドギャップを持つ半導体へと電子状態が変わる. これらは最初格子モデルの数値計算によって予言され,[2]-[4] 有効質量近似でも説明された.[5] すなわち, 図 1 (b)に示すようにFermi点（K点とK'点）がブリルアン域の中心ではないために, 周期境界条件を課すため円周を一周したときに, ブロッホ関数の余分な位相が付き, 包絡関数に対する境界条件は巻き方に依るのである. 詳細は既刊の書籍, 解説記事を参照いただきたい.[8]-[11] 最近ではSTMを使った観察により実験的にも確認されている.[6],[7] 磁場をナノチューブの軸に平行にかけると周期境界条件に余分の位相が付き, バンドギャップの大きさが振動する, すなわちAharonov-Bohm効果があらわれる.[5],[13] Peierls によって予言されたように, 一次元金属は安定でなく, 格子ひずみと電荷密度波を生じてギャップが開く. しかし, ナノチューブは例外である. 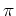電子の運動は一次元的であるが, ナノチューブが円筒であるために格子ひずみを生ずるエネルギーが大きすぎ, エネルギー的に不利だからである.[14],[16] また理論的には非常に細いナノチューブの場合, 曲率により $\pi$ 軌道間の結合が異方的となるため, 小さいギャップが予言されているが, 普通の太さのナノチューブではほとんど問題とならない.[2],[17]