last update 2007.11.22
Peppardらが報告した四つ組(テトラド)効果は、Jørgensenによって提唱された、Refined Spin-pairing Energy Theory (RSPET) と呼ばれる分光理論式に含まれる4f電子軌道の電子雲拡大効果が熱力学量として現れたものです。希土類元素の物理化学の最終章では、川邊によって熱力学量に適応できるように改良されたRSPETを中心に説明していきましょう。ただし、理工系の大学生レベルでないと理解できません(といっても私も高校で物理を専攻しなかったので皆さんと同じようなレベルです。間違いがあれば指摘してください)。
見たいエネルギーだけを見る
C. K. Jørgensen といえば、分光学ではかなり有名な人らしいです。特に 4f q→4fq+1 や4f q→4f q−15d エネルギー遷移をスピン-軌道相互作用の点から簡単に説明する式を提唱した事で知られています(Jørgensen, 1962, Mol. Phys. 5, 271-277; Jørgensen, 1963, Adv. Chem. Phys.. 5, 33-146; Jørgensen, 1970, J. Inorg. Nucl. Chem. 32, 3127-3128; Jørgensen, 1970, In Handbook on the Physics and Chemistry of Rare Earths, 3, 111-169.)。ただし、この人の論文はとにかく読みにくい(私はさっぱり理解できなかった)。お友達(?)のNugentさんが分かり易く説明している論文がありますので(Nugent L, J., 1970, J. Inorg. Nucl. Chem. 32, 3485-3491; Nugent and Sluis, 1971, J. Opt. Soc. Am. 61, 1112-1115; Nugent et al., 1971, J. Inorg. Nucl. Chem. 33, 2503-2530; Nugent et al., 1973, J. Phys. Chem. 77, 1528-1539)、興味のある方や分光学を専攻にしている方はこちらを読んでいただくとよろしいと思われます。この章で解説する内容は、Kawabe (1992, Geochem. J. 26, 309-335)を基本としていますので、ばりばりの物理化学を専攻されていない方はこちらを参考にしてください。
ランタノイドは、3d遷移金属元素と異なり結晶場による縮退した電子軌道の分裂の程度が小さく、むしろスピンー軌道相互作用による多重(LS)項の分裂の方が圧倒的に大きい特徴があります(例 足立,1999,希土類の科学)。もちろん、スピンースピン相互作用もありますが、これは結晶場の効果よりもさらに小さいものです。4f電子そのものが結合にほとんど関係しない(結合エネルギーのうち、4f電子軌道の電子が関係するのはほんの数%程度らしい)ことが、四組(テトラド)効果そのものの存在を疑問視する大きな理由となっているようです。しかし、相対値が小さいことは必ずしも、4f電子軌道が関係する結合エネルギーの絶対値が小さいことを意味しません。ただし、ランタノイドが様々な化合物を形成する中においても、4f電子の振る舞いが基本的にatomicであることがRSPETにおいて非常に重要となってくるあたりが、混乱を招く理由となっているかもしれません。
では本題に入りましょう。四つ組(テトラド)効果は4f電子が悪さをしていることは明かですので、まず、4f電子のエネルギーだけに着目してみましょう。4f電子の基底エネルギー(E(4f q))はRSPETより以下の式で表されます。
E(4f q) = qW0+(1/2)q(q −1){E0+(9/13)E1}+(9/13)n(S)E1 +m(L)E3+p(S, L, J)ζ4f (式 1)
W0は4f電子1個あたりの平均エネルギー、(E0, E1, E3)はラカー係数、ζ4f はスピン・軌道相互作用を表す定数項、n(S),m(L),p(S, L, J) は基底レベル(2S+1LJ )の量子数から決まる事実上の定数です。また、第3・4項に表われるラカー係数(E 1, E 3)は、電子反発エネルギーを表し、テトラド効果の大きさと向きを決める項です。これについては後ほど詳しく説明します。
式(1)は一見複雑怪奇で何が何だか分かりませんが、言わんとすることは単純明快です。まず式(1)の第1・2項は、基底エネルギーをキセノン核の周りに4f電子が均等に配置した時の平均的なエネルギーで表したものです。ただし、この二式は完全に理論的に値が与えられるものではなく、実際には実験データを元に決められます。次に、式(1)の第3-4項は、LS多重項を表します。一言で言うならば、フント則を反映したものです。第5項はスピン-軌道相互作用項を表します。ただし、第5項は寄与が小さい場合が多いので、多くの場合省略します。式(1)の言わんとすることは、「平均的なエネルギー(第1・2項)からフント則(第3-4項)によって基底エネルギーがさらに安定化する」と言うことです。
ちなみに、フント則とは
1つの電子状態からできる(L, S)準位の内でエネルギーが最低なのは(基底エネルギーを与える準位は)
のことを言います。
では、式(1)の第3・4項(LS多重項)による基底エネルギーの安定化傾向はランタノイドシリーズを通してどのように変化し、どのように四つ組(テトラド)効果につがるのでしょうか?それを表したのが下の表と図です。まず、n(S) とm(L)はいずれも負の定数です。n(S) にはV字型の変化が見られ、ガドリニウムブレイクの主要な原因となっています。一方、m(L)はW字型の変化を示します。そして、ラカー係数(E 1, E 3)の間には、ある一定比を取ることが経験的に知られていますので、その線形一次式(n(S)+(3/10) m(L))を求めてみると、なんとはっきりと四つ組(テトラド)効果が確認されます。従って、式(1)は、ランタノイド化合物の内部エネルギーに、四つ組(テトラド)効果が内在していることを示しているのです。
この説明ではよく分からないという方に、もう少し直感的に説明しましょう。4f電子軌道は7つありますが、同じ軌道に電子が2個ずつ(スピンの向きを逆にして)収納されるより、別々の軌道にスピンの向きを揃えて入った方が電子間の反発エネルギーは小さくなります(つまりより安定に)。この効果がn(S) のV字型変化となります。また、実際の4f電子軌道は球体状の軌道ではなく、ある方向に偏った存在確率分布を示します。そのため、空間的に近い軌道を避けて電子が収容される傾向があります。この効果が、m(L) のW字型変化につがると理解してください。もし、n(S)やm(L)の項がなければ、ランタノイドのエネルギーは、四つ組(テトラド)効果を持たない、なめらかな変化を示すはずです。
| Ln3+ | q | 基底状態 | n(S) | m(L) | p(S, L, J) |
|
| La | 0 | 1S0 | 0 | 0 | 0 | |
| Ce | 1 | 2F5/2 | 0 | 0 | −2 | |
| Pr | 2 | 3H4 | −1 | −9 | −3 | |
| Nd | 3 | 4I9/2 | −3 | −21 | −7/2 | |
| Pm | 4 | 5I4 | −6 | −21 | −7/2 | |
| Sm | 5 | 6H5/2 | −10 | −9 | −3 | |
| Eu | 6 | 7F0 | −15 | 0 | −2 | |
| Gd | 7 | 8S7/2 | −21 | 0 | 0 | |
| Tb | 8 | 7F6 | −15 | 0 | −3/2 | |
| Dy | 9 | 6H15/2 | −10 | −9 | −5/2 | |
| Ho | 10 | 5I8 | −6 | −21 | −3 | |
| Er | 11 | 4I15/2 | −3 | −21 | −3 | |
| Tm | 12 | 3H6 | −1 | −9 | −5/2 | |
| Yb | 13 | 2F7/2 | 0 | 0 | −3/2 | |
| Lu | 14 | 1S0 | 0 | 0 | 0 |
さて、式(1)は分光学の理論式から導かれた式ですから、次にこれを熱力学量に適応させる必要があります。ランタノイドが次のような化学反応式にある場合、
LnXm + nY y− = LnYn +mX x− 式(2)
反応のエンタルピーは次のように表されます。
ΔHr(q) =
ΔH 0f(LnYn)
+ mΔH 0f (X x−) −
ΔH 0f(LnXm) −
nΔH 0f(Y y−)
=
ΔH 0f(LnYn) −
ΔH 0f(LnXm) + constant. 式(3)
このとき、反応のエンタルピーは、4f電子の関係するエネルギー[ΔE( 4f q):式(1) ]とそれ以外のエネルギー[ΔH0 ]に分けることが出来ます。
ΔHr(q) = ΔE(4f q) + ΔH0 式(4)
次に、さらなる近似を導入します。式(1)で用いられた、W0, E0, E1, E 3, ζ4f は有効核電荷(Z* = q + s* ; s* = 25)に関係する量で、次のような近似式で表されます。もちろん、Δとは、反応前後のランタノイド化合物(化学種)の違いを表します。
ΔW0 = ΔW0(LnYn)
− ΔW0(LnXm) =
fw(q)Z* = (Cw + C'wq + ··· )(q
+ s*)
ΔE0 = ΔE0(LnYn) −
ΔE0(LnXm) =
fa(q)Z* 2 = (Ca + C'aq + ··· )(q + s*)2
ΔE1 = ΔE1(LnYn) −
ΔE1(LnXm) =
f1(q)Z* = (C1 + C'1q + ··· )(q + s*)
ΔE3 = ΔE3(LnYn) −
ΔE3(LnXm) =
f3(q)Z* = (C3 + C'3q + ··· )(q + s*)
Δζ4f = Δζ4f(LnYn) −
Δζ4f(LnXm) =
fls(q)Z* 4 = (Cls + C'lsq + ··· )(q +
s*)4. 式(5)
式(4)を元に、最終的に式(1)は有効核電荷の多項式で表されます。
ΔHr(q) = ΔH0 +
(a+bq)qZ* +
(9/13)n(S)C1Z* +
m(L)C3Z* +
p(S, L, J)ClsZ*4
= A + (a+bq)qZ* +
(9/13)n(S)C1Z* +
m(L)C3Z* +
p(S, L,
J)ClsZ*4 式(6)
細かい式の展開は省略しましたが、この式が熱力学量に現れた四組(テトラド)結果を表す、改良RSPET式です。A, a, b は定数項、C1 [≈ ΔE1/(q+s*)], C3 [≈ ΔE3/(q+s*)]はそれぞれラカー係数に関係した項、Cls [≈ Δζ4f /(q+s*) 4]はスピンー軌道相互作用項に関係した項です。通常の解析では、スピンー軌道相互作用項は大変小さいので無視します。
何とか、四組(テトラド)効果を理論式で表す事が出来ました。つぎに、エンタルピーの4f電子軌道以外の効果について少しお話ししていきましょう。1.希土類元素って?の 3.3. 希土類元素イオンで説明しましたランタニド効果によって、原子番号が増加するに従いランタノイドイオンはイオン半径が大きく変化します。このため、ランタノイド15元素全てが同じ配位構造を持つことは大変まれです。配位構造がランタノイド系列の途中で変わるということは、生成エンタルピーに、構造が変化することによって生じるエネルギー変化が組み込まれることになります。つまり、四組(テトラド)効果を解析する前に、この構造変化を適切に補正しておかないと(式(6)の定数項 A の補正)、正しい解析結果が得られなくなります。この構造変化補正について、具体例を挙げながら見ていきましょう。
Kawabe (1999)では、塩化ランタノイドn水和物(LnCl3・nH2O)とランタノイドエチルサルファイド9水和塩(Ln(C2H5SO4)3・9H2O)の熱力学データを用いた構造変化補正について議論しています。塩化ランタノイドはランタン(La)、セリウム(Ce)、プラセオジム(Pr)の化合物が7水和塩で残りが全て6水和塩です。これに対し、ランタノイドエチルサルファイド9水和塩はランタノイドシリーズ全てに共通した配位構造を持つ大変珍しい化合物です。従って、両者の生成エンタルピーの差に系統的な違いが見られた場合、それは塩化ランタノイドの水和数変化によって引き起こされたことになります。そこで、下記の式のような反応式を考え、反応のエンタルピーを求めてみましょう。
LnCl3・nH2O(c) + 3ES−(aq) + (9−n)H2O(l) = Ln(ES)3・9H2O(c) + 3Cl−(aq) 式(7)
下の図には青色で、式(7)の反応のエンタルピー変化を示しています["ES"は C2H5SO4の略称]。
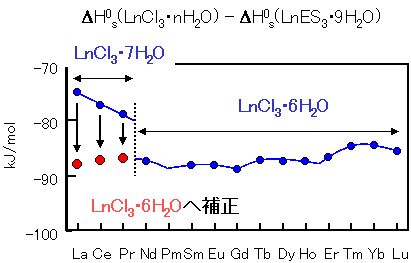
Kawabe (1999, Geochem. J. 33, 249-265)より引用(一部改)。
ごらんのように、プラセオジム(Pr)とネオジム(Nd)の間でギャップが生じています。これは水和数が途中で変化する(7から6へ)ために、塩化ランタンの持つ生成エンタルピーに余分なエネルギーが加わっているためです。RSPET式は、元々分光学データ解析用の理論式であるため、このような水和数(配位数)変化を補正する項目が入っておりません。そのため、この反応式を四組(テトラド)効果を改良RSPET式で解析するためには、塩化ランタノイドの水和数を全て同じにする必要があります。ここでは、水分子を一つ排出する反応エネルギーの補正を行えばよろしいのです。
LnCl3・7H2O(c) = LnCl3・6H2O(c) + H2O(l) 式(8)
この反応に伴うエネルギー変化を補正した結果が、上図の赤丸のデータです。補正することによって、ネオジム(Nd)の延長上にうまく曲線が引けそうです。残念ながら、地球上で起きる反応に改良RSPET式適応する場合は、この例のように簡単に構造変化が補正できる場合はあまり多くありません。上記例のような配位子の変化、結晶構造の変化、価数の変化など状況に応じて補正していきます。
さて、化学的な議論であれば、上記の改良RSPETで事が足りるのですが、地球化学においては、多くの議論が分配係数や錯生成定数など、エンタルピーではなくギブスの自由エネルギーしか、データとして利用できない場合があります。反応のギブスの自由エネルギーは、エンタルピーとエントロピーを用いて
ΔGr(q) = ΔHr(q) − TΔSr(q) 式(9)
と表されます。そこで、先ほどの式(7)の反応で得られる、ギブスエネルギー、エンタルピー、エントロピーに四組効果がどのように現れるかをまず見てみましょう。
右図には、式(7)の反応の熱力学量が示されています。当然ながら、水和数変化もギブスエネルギー、エンタルピー、エントロピー全てにそれぞれ対応した量ずつ補正されています。
ごらんのように、反応の熱力学量には全て四組(テトラド)効果が認められることが分かります。湾曲の強さに差はありますが、全て同じ向きに曲がっている事が分かります。従って、式(9)より、反応の温度が高い場合、エントロピーの四組(テトラド)効果とエンタルピーの四組(テトラド)効果が打ち消し会って、ギブスの自由エネルギーに四組(テトラド)効果が認められなくなってしまいます。右図に示したデータは25°Cの熱力学量ですが、この温度ですら、ギブスの自由エネルギーに見られる四組(テトラド)効果の程度がエンタルピーの四組(テトラド)効果に比べて小さいことが分かります。
このため、地球科学の分野で火山岩や深成岩など非常に高い温度(1000°C前後で反応した)で出来た物質には明瞭が四組(テトラド)効果が認められません。もし、2000-3000°Cの反応をみたならば、反応のギブスの自由エネルギーにはエントロピーの四組(テトラド)効果が強く反映されることでしょう。四組(テトラド)効果が見えたり見えなかったりすることから、四組(テトラド)効果は重要な現象ではない!という人も大勢います。しかし、温度が少しずつ下がってくると、花崗岩のような比較的低い温度で出来たと考えられる岩石には、四組(テトラド)効果が認められるようになります。見えないから重要でないと考えるのではなく、なぜ見えなくなるのだろう?と考えることが科学ではないのでしょうか?と私は思うのです。
さて、話が少しそれましたが、改良RSPETはエンタルピーに関する理論式です。もしエントロピーについて四組(テトラド)効果に関する理論式が確立されれば、自動的にギブスの自由エネルギーの四組(テトラド)効果に関する理論式が得られます。しかし、残念ながら現段階では論文としては、改良RSPETについてしか報告されていません。ではどうしましょう?
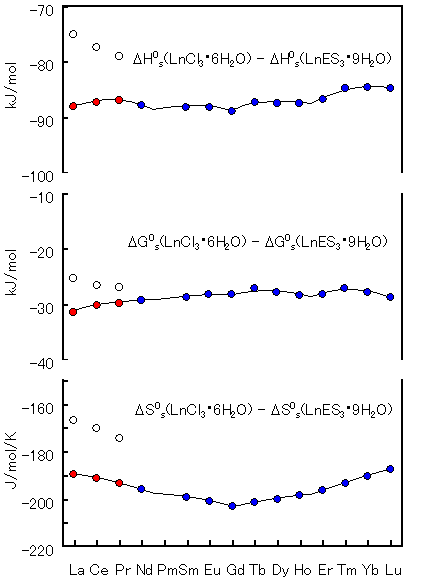
Kawabe (1999, Geochem. J. 33, 249-265)より引用(一部改)。
ここで、火山岩など非常に温度の高い反応は、エントロピーの四組(テトラド)効果に関する理論式が完成するまでしばらく定性的な議論をする事にし、河川や海など常温以下の低い温度で起きる反応に着目しましょう。この場合、ギブスの自由エネルギーはエンタルピー項だけでえいやっと近似してもよいと思われます。そこで、地球化学の研究で議論されている分配係数(Kd(Ln)) や錯体生成定数(K(Ln))に対して改良RSPET式(6)を適用してみましょう。ここで、反応式(2)の分配係数 K(Ln) (= {[LnYn]/[LnXm]}{[Xx−]m/[Yy−]n}:[ ]はモル分率を表す) を例に見ていきましょう。この場合、分配係数 K(Ln)は次のように書き直すことが出来ます。
log K(Ln) = − ΔGr /2.303RT
= {ΔGf(LnXm) −
ΔGf(LnYn)}/(2.303RT) + constant.
≈ {ΔHf(LnXm) −
ΔHf(LnYn)}/(2.303RT)+constant
≈ −{A + (a+bq)qZ* +
(9/13)n(S)C1Z* +
m(L)C3Z* +
p(S, L,
J)ClsZ*4}/(2.303RT) 式(10)
これが、地球化学の分野で使用する改良型のさらに改良型のRSPET式になります。反応のギブスの自由エネルギーと分配係数の間にはマイナスの関係がありますので、注意が必要です。ランタノイド化合物(錯体)以外による constant項や構造変化項は定数項 A に組み込んでいます。ΔGr(q) ≈ ΔHr(q) の仮定がありますので、式(10)で得られたC1, C3項は、当然ながらエンタルピーから得られる結果と完全には一致しません。しかし、大小関係や符号は一致します。
電子雲拡大効果(共有結合的?イオン結合的?それが重要)
では、最後に式(1)に出てきたラカー係数について説明しましょう。ラカー係数は分光学で使用される物理パラメーターで、電子雲拡大効果の程度を表します。分光学で見られるパラーメーターがどうして熱力学量に関係してくるのでしょう?この電子雲拡大効果を模式的に示したのが下の図です。
| イオン結合的 | 共有結合的 |
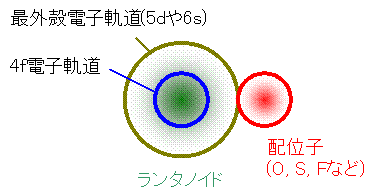 |
 |
| ラカー係数 大 | ラカー係数 小 |
| 4f電子は結合にほとんど寄与しないため、化合物であっても、まるで自由イオンと同じような電子軌道を示す。 | 結合に共有結合の度合いが強まると(あくまで相対的に)、4f電子軌道が配位子側へ広がる[電子雲拡大!]。これは、多少なりとも4f電子が結合に関与するためである。 |
 |
 |
| 4f電子の感じる電子反発(電子は負の電荷を持つため常に反発し合っている)は単独で存在する場合とほとんど変わらない。結果として、4f電子のエネルギー(式(1))に占めるテトラド効果の寄与は大きい。 | 4f電子の感じる電子反発エネルギーが減少するため、4f電子のエネルギー(式(1))に占めるテトラド効果の寄与が小さくなる。 |
つまり、イオン結合的なランタノイド化合物はラカー係数が大きくて、共有結合的なランタノイドの化合物はラカー係数が小さくなるということです。最も、ランタノイドは典型的なイオン結合的な化合物を作る元素ですので、あくまで相対的に共有結合性の寄与の大小を見ているわけです。実際の分光データからも、ネオジムの酸化物はフッ化物よりも共有結合性が高い化合物ですが、ラカー係数の大小関係も同様に、酸化物の方が小さくなっていることが分かります。と、いうことは、反応式を考えたとき、反応物と生成物の間のラカー係数の違いがテトラド効果として現れることになります。
次に、化学反応に内部エネルギー中のテトラド効果の差がどのように反映されるのかを、模式的に説明していきましょう。先ほどの式(7)と(8)を合わせた反応式
LnCl3・6H2O(c) + 3ES−(aq) + 3H2O(l) = Ln(ES)3・9H2O(c) + 3Cl−(aq) 式(11)
の反応のエンタルピーとRSPET式の関係は次のように表されます。
ΔHr(q) =
ΔH 0f(Ln(ES)3・9H2O(c)) −
ΔH 0f(LnCl3・6H2O(c)) + const.
= A + (a+bq)qZ*
+ (9/13)n(S)C1Z*
+ m(L)C3Z*
+ p(S, L,
J)ClsZ*4 式(12)
ここで、この反応のC1, C3パラメーターは、塩化ランタノイドn水和物(LnCl3・nH2O)とランタノイドエチルサルファイド9水和塩(Ln(C2H5SO4)3・9H2O) のもつそれぞれのラカー係数の差で表されます。4.2.3章の図に示した、反応のエンタルピーに上に凸のテトラド効果(上に向かってもこもこ)が認められるということは、C1, C3 パラメーターが正であることを示します。もし、C1, C3パラメーターが負である場合は、下に凸のテトラド効果が認められます。
C1 ≈ {ΔE1(Ln(ES)3・9H2O(c)) − ΔE1(LnCl3・6H2O(c)}/(q+s*) >0
: すなわち ΔE1(Ln(ES)3・9H2O(c)) >
ΔE1(LnCl3・6H2O(c))
C3 ≈ {ΔE3(Ln(ES)3・9H2O(c)) − ΔE3(LnCl3・6H2O(c)}/(q+s*) >0
: すなわち ΔE3(Ln(ES)3・9H2O(c)) >
ΔE3(LnCl3・6H2O(c))
結果として、塩化ランタノイドn水和物(LnCl3・nH2O)の方がランタノイドエチルサルファイド9水和塩(Ln(C2H5SO4)3・9H2O)よりもより共有結合性が高い化合物であることが分かります。
これをもっと一般化してみましょう。反応式(2)[LnXm + nY y− = LnYn + mX x−] を考えたとき、反応のエンタルピーに現れるテトラド効果には次の4つのパターンがあります。
| Cl ≈ {ΔEl(LnYn) − ΔEl(LnXm)}/(q+s*): l = 1 or 3 | ΔHr = ΔHf(LnYn) − ΔHf(LnXm) + const. | log K(Ln) = −ΔHr | ||
| C1, C3パラメーター | ΔEl (LnYn) (生成物): l = 1 or 3 | ΔEl (LnXn) (反応物): l = 1 or 3 | 反応のエンタルピーに現れるテトラド効果式(1)のE(4f)の模式図 | 分配係数に表れるテトラド効果 |
| ほとんど0(ゼロ) | 大(イオン結合的) | 大(イオン結合的) | テトラド効果がほとんど無い = 大きなテトラド効果(LnYn) − 大きなテトラド効果(LnXm) |
テトラド効果がほとんど無い |
| ほとんど0(ゼロ) | 小(共有結合的) | 小(共有結合的) | テトラド効果がほとんど無い = 小さなテトラド効果(LnYn) − 小さなテトラド効果(LnXm) |
テトラド効果がほとんど無い |
| 正 | 大(イオン結合的) | 小(共有結合的) | 上に凸のテトラド効果 [ = 大きなテトラド効果(LnYn) − 小さなテトラド効果(LnXm) |
下に凸のテトラド効果 |
| 負 | 小(共有結合的) | 大(イオン結合的) | 下に凸のテトラド効果 [ = 小さなテトラド効果(LnYn) − 大きなテトラド効果(LnXm) |
上に凸のテトラド効果 |
最後に、具体例を挙げながら見ていきましょう。さて、下の図は研究紹介のページでも載せた深海底マンガン団塊と海水間の希土類元素の分配反応についての研究結果です。青色は、天然のデータで、そのほかは鉄水酸化物と人工海水の間の希土類元素の分配実験の結果を示しています。縦軸の分配係数は、値が大きいほど鉄水酸化物にくっつきやすく、値が小さいほど海水中に留まりやすくなることを示しています。詳しくはOhta and Kawabe, 2000. Geochem. J., 34, 455-473を参照してください。
人工海水に炭酸イオンを入れない場合(一番下のデータ)は、重希土類元素が選択的に鉄水酸化物に取り込まれますが、軽希土類元素側はむしろ人工海水中に安定に存在します。これは重希土類元素ほど加水分解をしやすく沈殿しやすい性質を反映していることと、希土類元素が水に溶けているときの水分子の配位数が途中で変化し、軽希土類元素ほど溶液中で安定に存在しやすいことを反映しています。また、顕著な上に凸のテトラド効果が見られます。
人工海水に少しずつ炭酸イオンを加えていくと、どんどん軽希土類元素側の方が重希土類元素よりも選択的に鉄水酸化物に濃集していくことが分かります。これは、水に溶けている希土類元素が炭酸イオンと強く結びついてより安定に存在するためです。しかも、重希土類元素ほど炭酸イオンと強く結びついて安定になりやすいので、相対的に軽希土類元素上がり重希土類元素下がりの分配係数パターンになります。興味深いことに、炭酸イオンが増えていくとテトラド効果がどんどん小さくなり、最終的にはほとんど直線的になってしまいます (一番上のデータ、緑色のひし形)。これはどのように解釈すればよいのでしょうか?
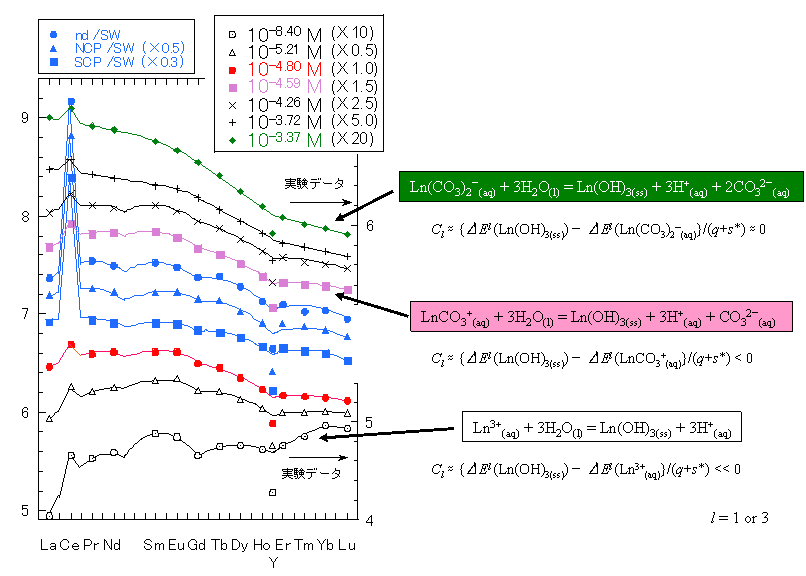
一番下の丸、中央のピンクの四角、一番上の緑色のひし形の3つのデータについて、それぞれ反応式を書いてみましょう。いずれの式も、生成物はLn(OH)3(ss)という鉄水酸化物に取り込まれた同じ化合物ですが、反応物側の(溶液中の)希土類元素は、溶液中の炭酸イオン濃度が増えていくに従って、次第にLn3+(aq)、LnCO3+(aq)、Ln(CO3)2−(aq) とどんどん変化していきます。この順に、共有結合性が増してゆき、最終的にはLn(CO3)2−(aq) とLn(OH)3(ss)では、ほとんどラカー係数が等しいためテトラド効果が見えなくなったと解釈できます。Ohta and Kawabe (2000) Geochem. J., 34, 455-473では、海底マンガン団塊と海水間の希土類元素の分配反応にはっきりと上に凸のテトラド効果が見られることから、海水中の希土類元素は基本的に従来考えられてきた結果とは異なり LnCO3+(aq) として存在していることを突き止めました。
また、Ohta and Kawabe. (2000) Geochim. Cosmochim. Acta, 65, 695-703では、水溶液中のpHが増加するに従って、二酸化マンガンと水溶液(炭酸イオンを含まない)間の希土類元素の分配係数に見られる上に凸のテトラド効果がより大きくなることから、pHの増加に伴って二酸化マンガンに取り込まれている希土類元素に配位している水酸基が増加したか、配位水和数が変化したかなど配位子場の変化が生じた結果と解釈しました。つまり、テトラド効果の向きや大小関係が化学種の推定に役立つことが分かります。
![]()