AIST Official Top Page Search result about Phase-field in AIST web site (Japanese)

フェーズフィールドモデル(PFM)に基づく二相流界面追跡CFD手法の研究・開発
Research and Development of Computational Fluid Dynamics (CFD) Methods Based on Phase-Field Model (PFM) for Interface-Tracking Simulations of Two-Phase Flows

国立研究開発法人 産業技術総合研究所
省エネルギー研究部門 熱流体システムグループ
 Thermal Energy Applications Group (TEA)
Recearch Institute for Energy Conservation (iECO)
National Institute of Advanced Industrial Science and Technology (AIST)
Tsukuba, Ibaraki, Japan.

連絡先/Contact Info.: 高田 尚樹 (Naoki TAKADA, Dr.Eng. E-mail: naoki-takada@aist.go.jp)
Last Update on July 30, 2023. / Articles [69,70] were added in References
S. Aihara, N. Takada & T. Takaki. Theor. Comput. Fluids Dyn. (2023).
高田尚樹, 化学工学, Vol. 87 (3) (2023), p. 126-128.
N. Takada, et al., Multiph. Sci. Technol., Vol. 34 (3) (2022), p. 17-33.
S. Aihara, T. Takaki & N. Takada. Comput. Fluids. 2019, Vol. 178, p. 141-151.
N. Takada et al. J. Comput. Sci., Vol. 17 (2016), p. 315-324.
【特集】フェーズフィールド法 (CMD Newsletter. 2015, No.53, p.2-17.)
【日本国内の企業・研究開発機関・教育機関の皆様へ連携研究のご案内】
　以下について当方共との連携をご検討の際は担当者(高田尚樹)へお気軽に御相談下さい。
（１）下記の熱・流体力学数値シミュレーション技術の研究開発
　　（物理モデル・数理モデル・計算スキーム・解析コード・アプリケーションソフトウェア）
（２）熱・流体現象の解明・予測・応用技術開発での下記シミュレーション技術の活用
Featured Publications: [66,65,62,54,39,43,40,29] for Key Technology:
Micro-fluidic Analysis Using Bottom-up Mesoscopic Models (PFM&LBM)
Micro Slug Droplets Motion Simulation
e.g. Simulator of micro droplets motion for MEMS device fabrication (CFD method54&Application6)
KAKENHI (Grants in Aid for Scientific Research), supported by MEXT & JSPS(3,4) BEANS Project, supported by NEDOGrant by NEDO(2) FIRST supported by MEXT & JSPS(3)
Micro Droplet Motion on Textured SurfaceMicro Droplet Motion on Textured Surface2D Broken Water Column under Gravity
Droplet on textured surface66| Droplet on partially wetted surface39| Water column under gravity32
Contents / 目次: 要約・キーワード/ 1.研究概要/ 2.PFM/ 3.数値実験結果/ 謝辞/ 参考文献
Abstract / 要約 :　このウェブサイトでは、空気、蒸気、水など多数種類の流体が混在して起こる複雑な物理現象を解明するための、流体力学と非平衡熱力学に基づく新しい数値流体力学（Computational Fluid Dynamics,CFD）シミュレーション手法の研究・開発の概要を紹介します。
　また、開発した手法を使用してコンピュータ上で再現される、水滴や液膜の界面（=水と空気の接触面）挙動の計算結果を、CG静止画像やMPEG形式動画で示します。[ English edition ]
Keywords / キーワード : Computational Fluid Dynamics, Nonequilibrium Thermodynamics, Numerical Analysis, Multiphase Flow, Two-Phase Flow, Bubble, Drop, Liquid Film, Lattice Boltzmann Method (LBM), Free Energy Theory, TDGL Equation, Cahn-Hilliard Equation, Allen-Cahn Equation, Phase-Field Model, Diffuse Interface Model, Surface Tension, Capillarity, Interface Tracking, Interface Capturing, Moving Boundary, Free Surface, Stefan Problem, Wettability, Contact Angle, Micro Channel, Phase Change, Boiling, Condensation, Vapor, Nucleation.
１．Introduction / 研究開発の概要 [11,22,25,29,32,37]

1.1. 目的 [ Revised on Aug.8,2006 ]
複雑二相流現象の高精度・高効率数値解析手法の基盤開発と現実問題への適用・普及．
(1) 高密度比二相流解析における，従来手法よりも高い計算効率と数値的安定性の実現．
(2) 解析ニーズに応じた時間・空間離散化スキームと計算アルゴリズムの柔軟な選択の実現．
(3) 体積・界面形状の保存性と界面再構成の高精度化．
(4) 格子ボルツマン法(Lattice Boltzmann Method, LBM)[8,15-21,35,36]の要素計算技術(物理モデル,離散化)と知見の活用．

1.2. 計算手法と研究開発の特徴 [ Revised on Aug.8,2006 ]
(1) 流体モデル・・・マルチスケール(界面＋流体)・マルチフィジックス(流体力学＋非平衡熱力学)
(2) 従来手法と異なる物理学的アプローチによる界面追跡/界面追跡アルゴリズム．
(3) 学術的新規性・・・数値流体力学(CFD)への材料計算科学分野の物理概念=フェーズフィールド・モデル(PFM)[1]-[7]の導入．
(4) LBMの二相流モデル[8,15-21,35,36]をベースにした研究開発の実施．
(5) 従来CFD手法の計算アルゴリズム・離散化スキームとPFMとの最適な融合．

1.3. 開発した計算手法の用途
高精度・高効率の流体数値実験の実施：
(1) 水域環境・地層環境中における流体挙動の微視的解明．
(2) 微視的流体現象を利用した環境改善技術の開発・評価．
(3) 流体挙動の高精度制御技術の開発・評価 (例:マイクロチャネル内二相流動)．
(4) 環境汚染物質の影響予測/拡散防止技術の開発・評価．

２．Phase-field Model(PFM) / フェーズフィールドモデルの概要

　界面を伴う多相・多成分物質系(二相流体,高分子薄膜,二元合金,etc.)で生じる，メゾスケールの複雑な組織形成過程を効率的に再現できる，自由エネルギー理論に基づく非平衡統計熱力学的モデル[1-5,28]．

2.1. 界面ダイナミクスの特徴[1,6-8,15,28,35,36]
(1) 界面 ＝ 流体の物性が連続的に変化する，有限な幅の領域(Diffuse Interface)．
(2) 表面張力 ＝ 秩序変数(質量密度or相・成分濃度)勾配に起因する，界面自由エネルギー．
　→界面形状に関する複雑な幾何計算(CSF model)を行わずに考慮される．
(3) 界面再構成 ＝ 非平衡系の化学ポテンシャルの瞬時局所的な勾配を利用．
　→従来アルゴリズム(MARS,CIP,etc.)を用いない，流体界面移流計算．

Table 1 Comparison of interface(I.F.)-tracking CFD methods [9,10]
Comparison of interface(I.F.)-tracking CFD methods

2.2. 二相流CFDに対する利点[1,6-11,28]
(1) 界面追跡計算の簡素化による, 計算コードの平易な多次元への拡張．
(2) 相変化や溶解に伴う, 界面を通した熱物質移動現象の自律的な再現．
(3) 固体表面の濡れ性境界条件の容易な実行．
(4) 複雑形状を持つ多数の界面に対する，従来よりも高効率な捕獲・追跡計算．
(5) 高密度比二相流(空気-水etc.)解析における，従来よりも高い数値的安定性．

2.3. 計算方法[6-11,54] [ Update on Aug.14,'13 ]
(1) 基礎方程式[1,8]
　(i) Navier-Stokes(NS)方程式系 ： 二相流体の質量,運動量,エネルギーの保存.
　(ii) 圧力テンソル ： 2階, 状態方程式 + 表面張力項, NS方程式に含まれる.
　(iii) Cahn-Hilliard(C-H)型[2]・Allen-Cahn(A-C)型方程式[47,48,50-54] ： 流体界面の移流・形成の計算.
(2) 空間の離散化と時間の進行方法
　(i) 空間 ： 有限差分法/有限要素法/有限体積法/境界適合座標.
　(ii) 時間 ： 陽解法(Runge-Kutta,修正Euler,改良Euler)/半陰解法/陰解法.
　(iii) その他 ： 格子ボルツマンスキーム[8,54]等, 既存の各種スキームが利用可能.
(3) アルゴリズム
　(i) 圧力・流速の計算 ： SMAC, SOLA, Projection法, etc.(非圧縮性流体)
　(ii) その他 ： CIP法など既存の各種アルゴリズムを併用可能.

３．Numerical Results / PFM-CFD法による二相流数値実験結果

(1) 円形界面 ( 直径=32正方形セル ) の非定常移流ベンチマーク計算 [9-11,12-14]
　・・・ 2次元, 一定角速度の回転, Courant数=2.5×10-3 【MPEG1動画, 575KB】
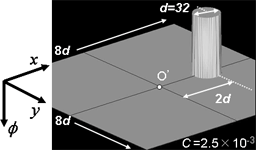　　2D rotation of an interface by a circular vortex with constant angular velocity.

(2) 自由落下液滴 ( 水, 直径10mm ) と液膜 ( 水, 厚さ2mm ) の衝突 [9][11][13]
　・・・ 2次元, 気相:空気, 常温1気圧, 界面形状, 流速ベクトル, 圧力分布 【MPEG1, 4.13MB】
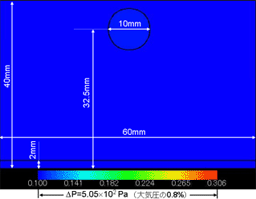　　2D single free-falling drop merging into a liquid film on solid wall.

(3) 自由落下液滴 ( 水, 直径10mm ) と液膜 ( 水, 厚さ2mm ) の衝突 [9][10][12-14]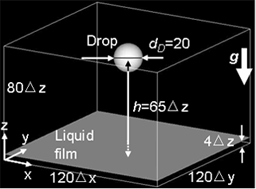
　・・・ 3次元, 気相:空気, 常温1気圧, 界面形状 【MPEG1, 1.43MB】
　　3D single drop free-falling and merging into a liquid film on solid wall.

(4) 自由落下液滴 ( 水, 10mm径 ) と液膜 ( 2mm厚 ) の衝突 [9][10][13][27]
　・・・ 3次元, 気相:空気, 常温1気圧 【MPEG1,2.41MB】
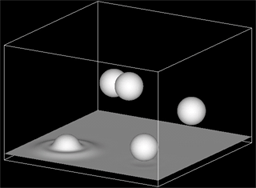　　3D free-falling drops merging into a liquid film on solid wall.

(5) 自由落下液滴 ( 水, 10mm径 ) と垂直液膜の衝突 [9]
　・・・ 3次元, 気相:空気, 常温1気圧 【MPEG1, 2.08MB】
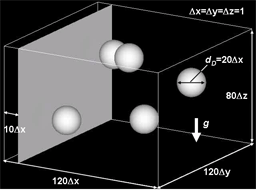　　3D free-falling drops collapsing with vertical liquid film.

(6) 固体表面上の不均一濡れ性による液滴 ( 水, 直径16mm半球 )の移動 [9]
　・・・ 3次元, 無重力, 気相:空気, 常温1気圧, 質量密度比801.7, 接触角:61.4度,118.6度.
　【MPEG1, 716KB】
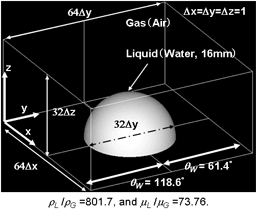　　3D motion of single drop on a flat surface of solid wall with non-uniform wettability (different contact angles).

(7) 液柱 ( 水, 高さ20mm×幅10mm×奥行10mm )の崩壊 [10][12-14][27]
　・・・ 2次元, 気相:空気, 常温1気圧, 奥行:周期境界条件 【MPEG1, 3.1MB】
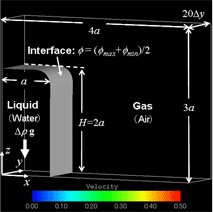　　Collapse of 2D liquid column under gravity.

(8) 液柱 ( 水, 高さ292mm×幅146mm )の崩壊 [10][12-14][27]
　・・・ 2次元, 気相:空気, 常温1気圧, 質量密度比801.7
　　Collapse of 2D liquid column under gravity.【GIF, 1.0MB】

(9) 過熱平板上での相変化による気泡核の形成 [7][12][15][31][37]
　・・・ van der Waals流体, 密度比1.53, 粘性・熱伝導=一定, 無重力, 2次元, 界面形状, 流速・温度分布.
　【MPEG1, 9.22MB】
　　2D bubble nucleation

(10) 一様せん断流れ場の液滴の変形・分裂[9][16]-[19][28] ( 格子ボルツマン法(LBM)の3次元二相流モデル[20][21]による結果 )
　・・・ 計算領域:64×32×64立方セル, 上下:移動壁境界(一定速度), その他:周期境界, 液滴直径16, 粘性比1, 密度比1, 3次元界面形状.
　Deformation and breakup of a single drop at Ca=0.3, Re=0.75.【MPEG1, 333KB】 Deformation and breakup of two drops at Ca=0.3, Re=1.0.【MPEG1, 929KB】

(11) Capillarity-driven air-water flow in a rectangular micro channel.
　・・・ 3D interface profile and cross-sectional flow velocity field. Contact angle 77 degrees, 0.1(D)×0.1(H)×0.2(W)mm, no gravity.
　Capillarity-driven air-water flow in a rectangular micro channel with 0.1(D)×0.1(H)×0.2(W)mm.【MPEG1, 1.22MB】

(12) 2次元円形界面 ( 直径=32正方形セル ) 線形移流ベンチマーク計算 [47,48,50,51,53-56]
　・・・ Courant数10-2, 移流方程式：修正保存形Allen-Cahn型, 計算スキーム：格子ボルツマン法. [ Addition on November 9, 2013. ]
　2D linear translation of an interface.【GIF動画, 920KB】

(13) T字型混合マイクロ流路による液液二相系スラグ液滴連続形成. ( 修正保存形拡散界面モデル[47,48,50,51,53-61] LBMによる結果. )
　・・・ 計算領域：462×22×82立方セル構造格子. 流路：正方形断面20×20セル, 親水性・滑り無し静止固体壁. 流入境界：断面一様速度. 流出境界：圧力一定, 速度勾配0. 流動条件：流量時間一定, 粘性比1, 密度比1, Reynolds数1.05, Capillary数2.53e-4, (a) 体積流量比 QO/QW = 1, (b) QO/QW = 1.5 (参考：実験(1,2,3)). [ Update on July 8, 2014. ]
(a)Two-phase liquid slug formation in microchannel with T-junction for Re=1.05 and Ca=2.53e-4.【WMV, 506KB】
(b)Micro Slug Droplets Motion Simulation

(14) 矩形流路内凹凸固体表面上の微小流体粒子の挙動予測. ( Phase-field LBM [47,48,50,51,53-61,66] による結果. )
　・・・ 計算領域：202×42×32立方セル構造格子. 流路：滑り無し静止固体壁, 溝深さ4セル幅, 静的接触角110°(液滴), 流量一定・一様流入, 連続流出. 半球状液滴直径32セル, 界面厚さ4セル幅, 粘性比1, 密度比1, Reynolds数13.37, Capillary数2.53e-3. [ Addition on August 23, 2014. ]
Two-phase liquid slug formation in microchannel with T-junction for Re=1.05 and Ca=2.53e-4. 【WMV, 598KB】
(a) 溝幅・間隔 4セル.
Two-phase liquid slug formation in microchannel with T-junction for Re=1.05 and Ca=2.53e-4. 【WMV, 612KB】
(b) 溝幅・間隔 6セル.
Two-phase liquid slug formation in microchannel with T-junction for Re=1.05 and Ca=2.53e-4. 【WMV, 357KB】
(c) 溝幅・間隔 8セル.

(15) 2次元等温物体周りのvan der Waals流体相変化流れ [37].
　・・・ 計算領域：300×60正方セル構造格子. Reynolds数2.03. [ Addition on August 23, 2014. ]
Two-phase liquid slug formation in microchannel with T-junction for Re=1.05 and Ca=2.53e-4.
(a) 計算領域, 初期・境界条件.
(b) 密度分布の時間変化. Cavitation数 0 (【WMV, 979KB】), 7 (【WMV, 675KB】).

(16) マランゴニ効果による温度勾配下の無重力静止液中の2次元単一気泡対流移動現象 [41].
　・・・ 計算領域：146×7×110立法セル構造格子, 気泡直径20セル, 密度比804.3，粘性比429.2，温度拡散比1.0, Marangoni数588.5, Prandtl数91.5, Weber数3.43e-2. 温度分布の時間変化. [ Addition on August 23, 2014. ]
2D bubble migration under temperature gradient and no gravity due to Marangoni effect for Ma=588.5, Pr = 91.5 and We=3.43e-2. 【WMV, 4.11MB】
Acknowledgements / 謝辞（代表者で獲得した主な研究資金）

(1) Financial support / 競争的外部研究資金: 「 微視的数値解析手法による地層環境内の物質拡散現象予測の高度化 」, 国立機関等原子力試験研究費, 文部科学省(MEXT), 平成14年度-16年度(2002/04/01-2005/03/31,終了). [ 概要(HTML), 事後評価資料(PDF,総合評価結果:A) ]

(2) Financial support / 競争的外部研究資金: 「 フェーズフィールドモデルに基づくマイクロ流路内二相流の界面追跡計算法の開発 」, 科学研究費補助金(Grant-in-Aid for Scientific Research)若手研究(B), 課題No.18760134, 文部科学省(MEXT), 平成18年度-20年度(2006/04/14-2009/03/31). [ 概要(PDF/HTML) ] [ Update on July 8, 2014. ]

(3) Financial support / 競争的外部研究資金: 「 フェーズフィールドモデルに基づくマイクロ多孔質体内相変化二相流計算法の開発 」, 科学研究費補助金(Grant-in-Aid for Scientific Research)基盤研究(C)（一般）, 課題No.26420128, 日本学術振興会(JSPS), 平成26年度-28年度(2014/04/01-2017/03/31). [ 概要(HTML) ] [ Addition on July 8, 2014. ]

(4) Financial support / 競争的外部研究資金: 「 微小流体操作デバイスの機能評価に向けた固気液混相流計算法の開発 」, 科学研究費補助金(Grant-in-Aid for Scientific Research)基盤研究(C)（一般）, 課題No.20K04297, 独立行政法人日本学術振興会(JSPS), 令和2年度-4年度(2020/04/01-2023/03/31). [ 概要(HTML) ] [ Addition on May 30, 2022. ]

References / 参考文献 [ [67] updated. ]

[1] Anderson, D. M.; McFadden, G. B.; Wheeler, A. A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, Vol. 30, p. 139-165. [ doi:10.1146/annurev.fluid.30.1.139 ][Abstract][ Up. Aug.23,2014 ]

[2] Cahn, J. W.; Hilliard, J. E. Free energy of a nonuniform system I. Interfacial free energy. J. Chem. Phys. 1958, Vol. 28, p. 258-267. [ doi: 10.1063/1.1744102 ][Abstract][ Up. Aug.23,2014 ]

[3] Dierk Raabe 原著, 酒井 信介・泉 聡志 共訳, "コンピュータ材料科学 - 材料の微視的構造と特性のシミュレーション -" (2004), 森北出版(株), ISBN978-4-627-66491-3. [概要][ Up. Aug.23,2014 ]

[4] 齊藤 良行, "組織形成と拡散方程式" (2000), (株)コロナ社, ISBN4-339-04349-4. [概要][ Up. Aug.23,2014 ]

[5] 太田 隆夫, "界面ダイナミクスの数理" (1997), (株)日本評論社, ISBN4-535-78246-6. [概要][ Up. Aug.23,2014 ]

[6] Jacqmin, D. Calculation of Two-Phase Navier-Stokes Flows Using Phase-Field Modeling. Journal of Computational Physics. 1999, Vol. 155, p. 96-127. [ doi:10.1006/jcph.1999.6332 ][Abstract][ Up. Aug.23,2014 ]

[7] Jamet, D.; Lebaique, O.; Coutris, N.; Delhaye, J. M. The Second Gradient Method for the Direct Numerical Simulation of Liquid-Vapor Flows with Phase Change. J. Comput. Phys.. 2001, Vol. 169, p. 624-651. [ doi:10.1006/jcph.2000.6692 ][Abstract][ Up. Aug.23,2014 ]

[8] Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys.. 2004, Vol. 198, p. 628-644. [ doi:10.1016/j.jcp.2004.01.019 ][Abstract][ Up. Aug.23,2014 ]

[9] 高田 尚樹. 二相流数値シミュレーションにおける界面追跡のためのフェーズフィールドモデルと格子ボルツマン法. 日本機械学会2004年度年次大会, 先端技術フォーラム, No.F06 : 熱流体解析技術の新展開−格子ボルツマン法−, 2004.9.7, 北海道大学.【 年次大会講演資料集(8),130-131. / 口頭発表資料(PFD) 】

[10] 高田 尚樹; 三澤 雅樹. 二相流界面追跡シミュレーションのためのフェーズフィールドモデルと格子ボルツマンスキームの検討. 日本流体力学会 第18回数値流体力学シンポジウム講演論文集(CD-ROM&Web,PDF), 論文No.D4-2, 国立オリンピック記念青少年センター(東京), 2004.12.15-17.

[11] 高田 尚樹; 冨山 明男. PHASE-FIELD MODELに基づく二相流数値計算手法. 日本機械学会論文集B編. 2005, 71巻, 701号, 論文No.04-0186, p. 117-124. [Contents][CiNii(Abstract&Text(PDF))][Full Text(PDF,Local)] [ doi:10.1299/kikaib.71.117 ]/ Takada, Naoki; Tomiyama, Akio. A Numerical Method for Two-Phase Flow Based on a Phase-Field Model. Transactions of the Japan Society of Mechanical Engineers, Series B ( Trans. Jpn. Soc. Mech. Eng. Ser. B ). 2005, Vol. 71, No. 701, Paper No.04-0186, p. 117-124. [ Up. Aug.23,2014 ]

[12] Takada, Naoki; Misawa, Masaki; Tomiyama, Akio. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Proceedings of 2005 ASME Fluids Engineering Division Summer Meeting and Exhibition (CD-ROM), Paper No. FEDSM2005-77367, June 19-23, 2005, Houston, Texas, USA. [ doi:10.1115/FEDSM2005-77367 ][Abstract][Abstract, in Forum on Advances in Free Surface and Interface Fluid...][ Up. Aug.23,2014 ]

[13] 高田 尚樹. フェーズフィールドモデルに基づく二相流界面追跡計算法. (社)自動車技術会 第8回CFD技術部門委員会 (講演資料,PDF,2.6MB), 2005/06/28, 市ケ谷, 東京.

[14] 高田 尚樹; 三澤 雅樹; 冨山 明男. 二相流界面追跡シミュレーションのためのフェーズフィールド法. 日本混相流学会年会講演会2005講演論文集, p.275-276, 講演No.C221, 一般セッションGS-3, 2005/08/02, 工学院大学, 新宿, 東京.【 要旨(PDF,578KB) 】

[15] Seta, T.; Kono, K. Thermal Lattice Boltzmann Method for Liquid-Gas Two-Phase Flows in Two Dimensions. JSME International Journal Series B-Fluids and Thermal Engineering. 2004, Vol. 47, No. 3, p. 572-583. [ doi:10.1299/jsmeb.47.572 ][Abstract] [ Up. Aug.23,2014 ]

[16] Takada, Naoki; Tomiyama, Akio; Hosokawa, Shigeo. Numerical Simulation of Drops in a Shear Flow by a Lattice-Boltzmann Binary Fluid Model. Computational Fluid Dynamics JOURNAL. 2003, Vol. 12, No. 3, p. 475-481. [Contents(HTML)][Text(PDF,proof)] [ Up. Aug.23,2014 ]

[17] 高田 尚樹; 冨山 明男. 統計熱力学的界面モデルを用いたせん断流中における液滴挙動の数値シミュレーション. 日本機械学会論文集B編. 2004, 70巻, 699号, 論文No.04-0121, p. 2712-2720. [Contents][CiNii(Abstract&Text)] [ doi:10.1299/kikaib.70.2712 ]/ Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Motion of Drops in a Shear Flow Using a Statistical-Thermodynamic Interface Model. Transactions of the Japan Society of Mechanical Engineers, Series B ( Trans. Jpn. Soc. Mech. Eng. Ser. B ). 2004, Vol.70, No.699, Paper No.04-0121, p. 2712-2720. [ Up. Aug.23,2014 ]

[18] Takada, Naoki; Tomiyama, Akio; Hosokawa, Shigeo. Lattice Boltzmann Simulation of Interfacial Deformation. International Journal of Modern Physics B ( Int. J. Mod. Phys. B ). 2003, Vol. 17, Nos. 1-2, p. 179-182. [ doi:10.1142/S0217979203017308 ][Abstract]

[19] Takada, Naoki; Tomiyama, Akio; Hosokawa, Shigeo. Lattice Boltzmann Simulation of Drops in a Shear Flow. Proceedings of the 4th ASME-JSME Joint Fluids Engineering Conference (CD-ROM), Paper No. FEDSM2003-45166, Honolulu, Hawaii, USA, July 6-10, 2003. [ doi:10.1115/FEDSM2003-45166 ][Abstract] [ Up. Aug.23,2014 ]

[20] Takada, Naoki; Misawa, Masaki; Tomiyama, Akio; Fujiwara, Shinya. Numerical Simulation of Two- and Three-Dimensional Two-Phase Fluid Motion by Lattice Boltzmann Method. Computer Physics Communications ( Comput. Phys. Commun. ). 2000, Vol. 129, Nos. 1-3, p. 233-246. [ doi:10.1016/S0010-4655(00)00110-7 ][Abstract]

[21] Takada, Naoki; Misawa, Masaki; Tomiyama, Akio; Hosokawa, Shigeo. Simulation of Bubble Motion under Gravity by Lattice Boltzmann Method. Journal of Nuclear Science and Technology ( J. Nucl. Sci. Technol. ). 2001, Vol. 38, No. 5, p. 330-341. [ doi:10.1080/18811248.2001.9715037 ][Abstract][CiNii][Full Text(PDF)] [ Up. Aug.23,2014 ]

[22] Takada, Naoki; Misawa, Masaki; Tomiyama, Akio. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Mathematics and Computers in Simulation ( Math. Comput. Simul. ). 2006, Vol. 72, Nos. 2-6, p. 220-226. [ doi:10.1016/j.matcom.2006.05.006 ][Abstract]

[23] 高田 尚樹. フェーズフィールド界面追跡法による水滴、水膜、水柱の動きのコンピュータシミュレーション. 日本機械学会 第18回計算力学講演会ビジュアリゼーションコンテスト, 2005/11/19-20, 筑波大学, つくば市.【 要旨(PDF,53KB) 】

[24] 高田 尚樹; 冨山 明男. フェーズフィールドモデルに基づく界面追跡法による高密度比二相流の数値シミュレーション. 日本流体力学会 第19回数値流体力学シンポジウム講演論文集(CD-ROM&Web,PDF), 講演No.B5-4, 国立オリンピック記念青少年センター(東京), 2005/12/13-15.【 要旨(PDF,449KB) 】

[25] 高田 尚樹; 三澤 雅樹; 冨山 明男. 二相流界面追跡シミュレーションのためのフェーズフィールド法. 混相流研究の進展. 2006, 1巻, p. 171-179. (日本混相流学会年会講演会2005論文精選集, 講演No.C221) [目次][要旨][本文(PDF)][参考文献]/ Takada, Naoki; Misawa, Masaki; Tomiyama, Akio. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Progress in Multiphase Flow Research ( Prog. Multiph. Flow Res. ). 2006, Vol. 1, p. 171-179. [ doi:10.3811/pmfr.1.171 ][Contents][Abstract][Text(PDF)][Refs.] [ Up. Aug.23,2014 ]

[26] 高田 尚樹; 冨山 明男. フェーズフィールドモデルに基づく界面追跡法の自由表面流れ解析への適用. 第55回理論応用力学講演会(NCTAM2006)講演論文集, p. 277-278, 講演No.2D02, 2006/01/25, 京大会館, 京都市左京区.【 要旨(PDF/HTML) 】 [ Up. Aug.23,2014 ]

[27] Takada, Naoki; Tomiyama, Akio. Interface-Tracking Simulation of Two-Phase Flows by Phase-Field Method. Proceedings of 2006 ASME Joint U.S.-European Fluids Engineering Summer Meeting (CD-ROM), Paper No. FEDSM2006-98536, July 17-20, 2006, Miami, Florida, USA. [ Forum on Advances in Free Surface and Interface Fluid Dynamics ][ doi:10.1115/FEDSM2006-98536 ][Abstract] [ Up. Aug.23,2014 ]

[28] 日本機械学会 編 (分担執筆), "改訂 気液二相流技術ハンドブック," p. 88-92, A5判, 604頁, ISBN978-4-339-04578-9, 株式会社コロナ社, 2006年6月30日./ The Japan Society of Mechanical Engineers, "Handbook of Gas-Liquid Two-Phase Flow Technology - Second Edition," 3.4.4 Numerical Analysis of Multi-phase Flows by Using Lattice Boltzmann Method (ed. N.Takada, p. 88-92), A5, 604 pages, ISBN978-4-339-04578-9, Corona Publishing Co., Ltd., Tokyo, Japan, June 30, 2006 (in Japanese). [ Up. Aug.23,2014 ]

[29] Takada, Naoki; Tomiyama, Akio. A Numerical Method for Two-Phase Flow Based on a Phase-Field Model. JSME International Journal Series B-Fluids and Thermal Engineering ( JSME Int. J. Ser. B-Fluids Therm. Eng. ). 2006, Vol. 49, No. 3, p. 636-644. [ doi:10.1299/jsmeb.49.636 ][Contents][Abstract][Full Text(PDF)][Refs.][CiNii] [ Up. Aug.23,2014 ]

[30] 高田 尚樹; 広川 景俊; 林 公祐; 冨山明 男. 二相流数値シミュレーションの界面移流・再構成計算に対するカーン・ヒリアード方程式の適用性の検討. 第11回日本計算工学会講演会(JSCES2006), 計算工学講演会論文集, 第11巻第1号, p. 415-416, 講演No.C-5-1, 2006/06/12-14, 大阪大学コンベンションセンター, 大阪府吹田市.

[31] 高田 尚樹; 冨山 明男. フェーズフィールド法を用いた相変化を伴う二相流の数値シミュレーション. 日本混相流学会年会講演会2006講演論文集, p. 420-421, 講演No.D322, 2006/08/04-06, 金沢工業大学, 石川県.【 要旨(PDF,362KB) 】

[32] Takada, Naoki; Tomiyama, Akio. Application of Interface-Tracking Method Based on Phase-Field Model to Numerical Analysis of Free Surface Flow. Theoretical and Applied Mechanics Japan ( Theor. Appl. Mech. Jpn., Proceedings of NCTAM Japan ). 2006, Vol. 55, p. 149-156. [ doi:10.11345/nctam.55.149 ][Abstract][Full Text(PDF,Local)] [ Update on June 28, 2013 ]

[33] 林 公祐; 高田 尚樹; 冨山 明男. 表面張力評価へのカーン-ヒリヤード方程式の応用. 日本機械学会第18回計算力学講演会講演論文集, p. 805-806, 講演No.2504, 2005/11, 筑波大学, 茨城県つくば市. [ Up. Aug.23,2014 ]

[34] 林 公祐; 高田 尚樹; 冨山 明男. 表面張力評価へのカーン-ヒリヤード方程式の応用. 混相流. 2006, 20巻, 3号, p. 244-251. [CiNii][Contents][Abstract][Text(PDF)][Refs.]/ Hayashi, Kosuke; Takada, Naoki; Tomiyama, Akio. Application of Cahn-Hilliard Equation to the Evaluation of Surface Tension Force. Japanese Journal of Multiphase Flow ( Jpn. J. Multiph. Flow ). 2006, Vol. 20, No. 3, p. 244-251. [ doi:10.3811/jjmf.20.244 ] [ Up. Aug.23,2014 ]

[35] Swift, M. R.; Orlandini, E.; Osborn W. R.; Yeomans, J. M. Lattice Bolztammn Simulations of Liquid-Gas and Binary Fluid Systems. Physical Review E. 1996, Vol.54, p. 5041-5052. [ doi:10.1103/PhysRevE.54.5041 ][Abstract]

[36] Teng, S.; Chen, Y.; Ohashi, H. Lattice Boltzmann Simulation of Multiphase Fluid Flows through the Total Variation Diminishing with Artificial Compression Scheme. International Journal of Heat and Fluid Flow. 2000, Vol. 21, p. 112-121. [ doi:10.1016/S0142-727X(99)00068-5 ][Abstract]

[37] 高田 尚樹; 冨山 明男. フェーズフィールド法を用いた相変化を伴う二相流の数値シミュレーション. 混相流研究の進展. 2007, 2巻, p. 173-180. (日本混相流学会年会講演会2006論文精選集) [目次][要旨][本文(PDF)][参考文献]/ Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Two-Phase Flows with Phase Change Using a Phase-Field Method. Progress in Multiphase Flow Research ( Prog. Multiph. Flow Res. ). 2007, Vol. 2, p. 173-180. [ doi:10.3811/pmfr.2.173 ][Contents][Absract][Text(PDF)][Refs.] [ Up. Aug.23,2014 ]

[38] Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Isothermal and Thermal Two-Phase Flows Using Phase-Field Modeling. International Journal of Modern Physics C ( Int. J. Mod. Phys. C ). 2007, Vol.18, No.4, p. 536-545. [ doi:10.1142/S0129183107010772 ][Abstract]

[39] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Ichikawa, Naoki. Application of a Phase-Field Method to the Numerical Analysis of Motions of a Two-phase Fluid with High Density Ratio on a Solid Surface. Journal of Computational Science and Technology. 2008, Vol.2, No.2 (Special Issue on Computational Methods for Multiphase Flows), p. 318-329. [ doi:10.1299/jcst.2.318 ][Contents][Abstract][Full Text(PDF)][Refs.][Preface]

[40] Matsumoto, Junichi; Takada, Naoki. Two-phase flow analysis based on a phase-field model using orthogonal basis bubble function finite element method. International Journal of Computational Fluid Dynamics ( Int. J. Comput. Fluid Dyn. ). 2008, Vol. 22, No. 8, p. 555-568. [ doi:10.1080/10618560802238226 ][Abstract][AIST RRPDB]

[41] 高田 尚樹; 松本 純一. 拡散界面モデルを用いた二相流体流れの数値解析. 数理解析研究所講究録 (数値解析における理論・手法・応用). 2009, Vol. 1638 (20090400), p. 83-94. [CiNii][Handle Proxy(Image PDF)] / Takada, Naoki; Matsumoto, Junichi. Numerical Analysis of Two-phase Fluid Flows Using a Diffuse-interface Model. RIMS Kokyuroku. 2009, Vol. 1638, p. 83-94.

[42] 松本 純一; 高田 尚樹; 松本壮平. Phase-Fieldモデル自由表面問題におけるCahn-Hilliard方程式の陰的混合有限要素法の検討. 日本流体力学会 第23回数値流体力学シンポジウム講演論文集(CD-ROM). 論文No.G9-6, 2009/12/18, 仙台市民会館, 宮城県仙台市. [要旨(PDF)]

[43] 井上 康博; 松本 迪斉; 北條 正樹; 高田 尚樹; 安達 泰治; 石田和希. Phase-Field Navier-Stokesモデルによる繊維間隙スケール樹脂流れにおける気液界面ダイナミクスの検討. 日本複合材料学会誌. 2010, Vol. 36, No. 3, p. 94-103. [要旨]/ INOUE, Yasuhiro; MATSUMOTO, Michihito; HOJO, Masaki; TAKADA, Naoki; ADACHI, Taiji; ISHIDA, Kazuki. Simulation Study on Dynamics of Resin-Air Interface during Resin-Air Flows between Filaments Using Phase-Field Navier-Stokes Model. Journal of the Japan Society for Composite Materials. 2010, Vol. 36, No. 3, p. 94-103. [ doi:10.6089/jscm.36.94 ][Contents][Abstract][Text(PDF)][Refs.][CiNii]

[44] 松本 純一; 高田 尚樹. 気液の二相流れ数値シミュレーション. 特集・トライボロジーにおける最新計算手法. 2010, トライボロジスト, 55巻, 6号, p. 387-393. [CiNii]/ MATSUMOTO, Junichi; TAKADA, Naoki. Numerical simulations of gas-liquid two-phase flow. Toraiborojisuto/Journal of Japanese Society of Tribologists. 2010, Vol. 55, No. 6, p. 387-393. [AIST RRPDB] [ Up. Aug.23,2014 ]

[45] 松本 純一; 高田 尚樹; 松本 壮平. Phase-Fieldモデルを用いた一億自由度気液二相流有限要素解析. 第60回理論応用力学講演会, 2011/03/08, 東京工業大学, 東京都目黒区大岡山./ Matsumoto, J.; Takada, N.; Matsumoto, S. One Hundred Million Degree of Freedom Two-Phase Flow Finite Element Method Analysis Using Phase-Field Model. Proceedings of the 60th National Congress on Theoretical and Applied Mechanics (NCTAM). 2011, Vol.60, Paper No.GS03-04. [Abstract][AIST RRPDB]

[46] 高田 尚樹; 松本 純一; 松本 壮平. Phase-fieldモデルを援用した混相流のCFDシミュレーション. 化学工学会関東支部 第7回ホットな話題の講習会「高度部材開発を支えるCFDシミュレーション」, 2012/05/09, 東京理科大学森戸記念館第一フォーラム, 東京都新宿区. 講習会テキスト, p. 14-26. [AIST RRPDB]

[47] 高田 尚樹; 松本 純一; 松本 壮平. 混相流体力学数値シミュレーションのための保存形拡散界面モデルに基づく移動境界追跡法. 日本機械学会第25回計算力学講演会, 講演No.1121 (OS 11. フェーズフィールド法とその多様な展開), 2012/10/07, ポートアイランド南地区, 兵庫県神戸市中央区./ Takada, N.; Matsumoto, J.; Matsumoto, S. A moving boundary-tracking method based on a conservative diffuse-interface model for computational multiphase fluid dynamics simulations. Proceedings of JSME 25th Computational Mechanics Conference (CMD2012). 2012, Paper No.1121, Port Islad, Kobe, Hyogo, Japan. [AIST RRPDB]

[48] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. Phase-field Model-based Simulation of Motions of a Two-phase Fluid on Solid Surface. JSME-CMD International Computational Mechanics Symposium 2012 in Kobe (JSME-CMD ICMS2012), No.MS7-4-2 (Minisymposium: No.7 Recent Progress in Computational Fluid Dynamics and Related Topics), 2012/10/9-11, Port Island, Kobe, Hyogo, Japan. [AIST RRPDB]

[49] 高田 尚樹; 松本 純一; 松本 壮平. MEMS流体デバイス設計等のためのマイクロスケール混相流体シミュレーション技術. 産総研オープンラボ (AIST OpenLab), テーマNo.N-95, 2012/10/25-26, 産業技術総合研究所つくばセンター, 茨城県つくば市. 研究カタログ, 2012年度版, p.352. [Abstract(digbook)][AIST RRPDB]

[50] 高田 尚樹; 松本 純一; 松本 壮平. 保存形拡散界面モデルに基づく二相流体移流方程式の数値解法. 日本流体力学会第26回数値流体力学シンポジウム講演論文集(USB Memory&Web,PDF), 講演No.B03-2, 国立オリンピック記念青少年総合センター (東京都渋谷区), 2012/12/18-20./ Takada, N.; Matsumoto, J.; Matsumoto, S. A numerical method for two-phase fluid advection equation based on a conservative diffuse-interface model. Proceedings of JSFM 26th Computational Fluid Dynamics Symposium (CFD2012). Paper No.B03-2, December 18-20, 2012, Tokyo, Japan. [Proc.Paper(PDF)][AIST RRPDB]

[51] 高田 尚樹; 松本 純一; 松本 壮平. 二相流体流れシミュレーションのための保存形拡散界面移流方程式の数値解法. 第62回理論応用力学講演会講演論文集(USB Memory&Web,PDF), 講演No., 東京工業大学大岡山キャンパス (東京都目黒区), 2013/03/06-08./ Takada, N.; Matsumoto, J.; Matsumoto, S. A numerical method to conservative diffuse-interface advection equation for two-phase fluid flow simulations. Proceedings of 62nd Theoretical and Applied Mechanics Japan (NCTAM). Paper No., March 6-8, 2013, Tokyo, Japan. [Abstract][AIST RRPDB]

[52] 松本 純一; 高田 尚樹; 松本 壮平. 非構造格子を用いたPhase-Fieldモデル自由表面問題におけるAllen-Cahn方程式の計算法の検討. 第18回計算工学講演会講演論文集, 講演No.F-9-1(OS32自由移動境界問題(2)), 東京大学生産技術研究所 (東京都目黒区駒場), 2013/06/20./ Matsumoto, J.; Takada, N.; Matsumoto, S. A Study on Computational Method of Allen-Cahn Equation in Phase-Field Model Free Surface Problem using Unstructured Grid. Proceedings of Computational Engineering and Science, Vol. 18, Paper No.F-9-1, June 19-21, 2013, Institute of Industrial Science, the University of Tokyo, Komaba, Tokyo, Japan.

[53] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. A Diffuse-interface Tracking Method for the Numerical Simulation of Motions of a Two-phase Fluid on a Solid Surface. Proceedings of the 8th International Conference on Multiphase Flow (ICMF2013), Paper ID: ICMF2013-599, May 26-31, 2013, Jeju, Korea. [AIST RRPDB]

[54] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. Phase-field Model-based Simulation of Motions of a Two-phase Fluid on Solid Surface. Journal of Computational Science and Technology. 2013, Vol. 7, No. 2, p. 322-337. (Special Issue on International Computational Mechanics Symposium, 2012 (ICMS2012), Kobe) [ doi:10.1299/jcst.7.322 ][Abstract][AIST RRPDB]

[55] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. An Interface-tracking Method based on a Conservative Phase-field Model for Computational Two-phase Fluid Dynamics Simulations. The 5th International Conference on Coupled Problems in Science and Engineering (Coupled Problems 2013). June 19, 2013, Santa Eulalia, Ibiza, Spain. [Abstract(PDF)][AIST RRPDB]

[56] 高田 尚樹; 松本 純一; 松本 壮平. 修正保存形拡散界面モデルに基づくマイクロ二相流数値計算手法. 第26回計算力学講演会講演論文集, 講演No.1620 (OS 16. フェーズフィールド法とその多様な展開), 佐賀大学 (佐賀市本庄町), 2013/11/02./ Takada, N.; Matsumoto, J.; Matsumoto, S. A Numerical Method for Micro Two-phase Fluid Flow Based on a Modified Conservative Diffuse-interface Model. Proceedings of 26th Computational Mechanics Conference (CMD2013). Paper No.1620, November 2, 2013, Saga, Japan. [Program][AIST RRPDB] [ Update on August 13, 2014 ]

[57] 松本 純一; 高田 尚樹. 非構造格子を用いたPhase-Fieldモデル自由表面問題における化学ポテンシャルとモビリティーの効果の検討. 第26回計算力学講演会講演論文集, 講演No.1621 (OS 16. フェーズフィールド法とその多様な展開), 佐賀大学 (佐賀市本庄町), 2013/11/02./ Matsumoto, J.; Takada, N. A Study of the Effects of Mobility and Chemical Potential in Phase-Field Model Free Surface Problem using Unstructured Grid. Proceedings of 26th Computational Mechanics Conference (CMD2013). Paper No.1621, November 2, 2013, Saga, Japan. [Program][AIST RRPDB] [ Update on August 13, 2014 ]

[58] 高田 尚樹; 松本 純一; 松本 壮平. マイクロ製造プロセスにおける二相流体挙動の拡散界面モデルに基づく数値計算手法. 第5回マイクロ・ナノ工学シンポジウム講演論文集, p. 155-156, 講演No.6PM1-D-4 (OS.6PM1-D マイクロナノ現象のシミュレーション), 仙台国際センター (宮城県仙台市青葉区), 2013/11/06./ Takada, N.; Matsumoto, J.; Matsumoto, S. A Numerical Method Based on Diffuse-interface Model for Two-phase Fluid Motion in Microfabrication Process. Proceedings of 5th Micro Nano Engineering Symposium (MNM2013), p.155-156, Paper No.6PM1-D-4, November 6, 2013, Sendai, Miyagi, Japan. [Program(PDF)][AIST RRPDB] [ Update on August 13, 2014 ]

[59] 高田 尚樹; 松本 純一; 松本 壮平; 三鬼 陽美; 金子 暁子; 阿部 豊. T型混合部を有するマイクロ流体デバイス内の液滴形成に関する数値シミュレーション. 日本流体力学会第27回数値流体力学シンポジウム講演論文集(USB Memory&Web,PDF), 講演No.D08-3 (OS2-3: 離散要素型解法), 名古屋大学 (愛知県名古屋市千種区), 2013/12/17-19./ Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Miki, Youmi; Kaneko, Akiko; Abe, Yutaka. Numerical Simulation of Formation of Liquid Droplets in Microfluidic Device with T-junction. Proceedings of JSFM 27th Computational Fluid Dynamics Symposium (CFD2013), Paper No.D08-3, December 17-19, 2013, Nagoya University, Nagoya, Aichi, Japan. [Program/Proc.Paper(PDF)][AIST RRPDB] [ Update on December 1, 2014 ]

[60] 高田 尚樹; 松本 純一; 松本 壮平. 固体表面上の二相流体挙動の数値解析へのPhase-fieldモデル格子ボルツマン法の適用. 日本計算工学会 第19回計算工学講演会論文集(CD-ROM), 講演No.B-5-3 (OS 3. 計算工学におけるフェーズフィールド法の可能性), 広島国際会議場 (広島市中区中島町), 2014/06/11-13./ Takada, N.; Matsumoto, J.; Matsumoto, S. Application of a Phase-field Model-based Lattice Boltzmann Method to Numerical Analysis of Two-phase Fluid Motion on Solid Surface. Proceedings of the Conference on Computational Engineering and Science, Vol. 19, Paper No.B-5-3, June 11-13, 2014, Hiroshima, Japan. [AIST RRPDB] [ Addition on August 13, 2014 ]

[61] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. Numerical Simulation of Two-phase Fluid Motion in Microchannel Based on Phase-field Model. Proceedings of the 11th World Congress on Computational Mechanics (WCCM XI - ECCM V - ECFD VI), p. 3895-3903, Paper No. 2182, July 20-25, 2014, Barcelona, Spain. [Program(MS143B)][Abstract][Paper][AIST RRPDB] [ Update on October 8, 2014 ]

[62] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. A Diffuse-interface Tracking Method for the Numerical Simulation of Motions of a Two-phase Fluid on a Solid Surface. The Journal of Computational Multiphase Flows. 2014, Vol. 6, No. 3, p. 283-298. [ doi:10.1260/1757-482X.6.3.283 ][Contents][Abstract][AIST RRPDB] [ Update on October 11, 2014 ]

[63] 高田 尚樹; 松本 純一; 松本 壮平; 栗原 一真. 物体の形状と表面濡れ性に起因する微小二相流体挙動の数値シミュレーション. 日本流体力学会第28回数値流体力学シンポジウム講演予稿集, 講演No.D05-1 (OS2-3: 離散要素型解法), タワーホール船堀 (東京都江戸川区), 2013/12/09-11./ Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Kurihara, Kazuma. Numerical Simulation of Microscopic Two-phase Fluid Motion Caused by Solid-body Shape and Surface Wettability. Proceedings of JSFM 28th Computational Fluid Dynamics Symposium (CFD2014), Paper No.D05-1, December 9-11, 2014, Tower Hall Funabori, Edogawa-ku, Tokyo, Japan. [Program/Proc.Paper(PDF)][AIST RRPDB] [ Update on October 5, 2015 ]

[64] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Kurihara, Kazuma. CFD Simulation of Microscopic Two-phase Fluid Motion on Solid Body with Edges and Heterogeneously-wetted Surface Using Phase-field Model. Proceedings of the 6th International Conference on Coupled Problems in Science and Engineering (Coupled Problems 2015), p. 625-634, Paper ID 320, May 18-20, 2015, San Servolo, Venice, Italy. [Program(WeE03)][Abstract(PDF)][Full paper(PDF)][AIST RRPDB] [ Addition on October 5, 2015 ]

[65] Inoue, Yasuhiro; Ishida, Kazuki; Takada, Naoki; Hojo, Masaki. Reductions in anisotropic errors from implementation of phase-field wetting boundary condition for off-grid objects. International Journal of Computational Methods (Int. J. Comput. Meth.). 2015, Vol. 12, No. 6, 1550042. [ doi:10.1142/S0219876215500425 ][Abstract][AIST RRPDB] [ Addition on October 5, 2015 ]

[66] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Kurihara, Kazuma. Phase-field model-based simulation of two-phase fluid motion on partially wetted and textured solid surface. Journal of Computational Science (J. Comput. Sci.). 2016, Vol. 17, Part. 2, p. 315-324. [ doi:10.1016/j.jocs.2016.05.009 ][Abstract][Google][AIST RRPDB] [ Addition on January 3, 2017 ]

[67] Aihara, Shintaro; Takaki, Tomohiro; Takada, Naoki. Multi-phase-field modeling using a conservative Allen-Cahn equation for multiphase flow. Computers & Fluids ( Comput. Fluids ). 2019, Vol. 178, p. 141-151. [ doi:10.1016/j.compfluid.2018.08.023 ][Abstract][AIST RRPDB][ Addition on February 7, 2019 ]

[68] Takada, Naoki; Mogi, Katsuo; Takaki, Tomohiro; Someya, Satoshi; Baba, Soumei; Saito, Shimpei. Microfluidic simulations of droplet motion on structured solid surface using phase-field lattice Boltzmann method. Multiphase Science and Technology (Multiph. Sci. Technol.). 2022, Vol. 34, No. 3, p. 17-33. [ doi:10.1615/MultScienTechn.2022043657 ][Abstract][Researchmap][ Update on November 6, 2022 ]

[69] 高田 尚樹. フェーズフィールド法による混相流の数値流体力学シミュレーション. 化学工学. 2023, 87巻, 3号, 特集:化学工学における流体シミュレーションの実践〜2030年に向けた化学工学系流体シミュレーション：part 2〜, p. 126-128. [目次/趣旨][要旨] [ Addition on July 30, 2023 ]

[70] Aihara, Shintaro; Takada, Naoki; Takaki, Tomohiro. Highly conservative Allen-Cahn-type multi-phase-field model and evaluation of its accuracy. Theoretical and Computational Fluid Dynamics (Theor. Comput. Fluid Dyn.). 2023, Vol. 37, in press. [ doi:10.1007/s00162-023-00655-0 ][Abstract][Full Text(PDF)][Researchmap] [ Addition on July 30, 2023 ]

Links / ウェブリンク

フェーズフィールド法 - Phase-Field Method -
フェーズフィールド法に関する情報発信ウェブページ

格子ボルツマン法 - Lattice Boltzmann Method (LBM) -
[ Update on November 6, 2022. ]

Last Update on July 30, 2023.
Copyright © 2001-2023 by Naoki TAKADA (AIST), All Rights Reserved.
E-mail (Webmaster): naoki-takada@aist.go.jp
Access : access counter since October 21, 2004.
( Result(2005-'06)/ 1,000views in start-Aug.5,'05
/ 2,000 (-Jun.18,'06) / 3,000 (-Mar.18,'07) / 5,000 (-July 11,'08) )
 		AIST Official Top Page
AIST Official Top Page (English Edition) Search result about Phase-field in AIST web site (English)