last update 2018.06.20
第2回では、X線の吸収スペクトルに現れるへんてこな波々構造についてお話ししていきます。
第1回では大まかなX線の吸収構造について紹介し、その特徴が物質によるX線の散乱と吸収によって生じることを説明しました。次に、KまたはL吸収端をもっと細かく見ていきましょう。まずX線の吸収スペクトルの内、K吸収端付近をどんどん拡大してみましょう。するとどうでしょう。なにやらギザギザの波打ち構造が見えてきました。このように、非常に微細(微少)な構造の事をX線吸収微細構造(そのまんまですが・・・)と呼びます。ちなみに、英語では x-ray absorption fine structure といい、頭文字を取って略して XAFS と呼びます。ちなみに、吸収の構造をまとめてスペクトルと呼びます。
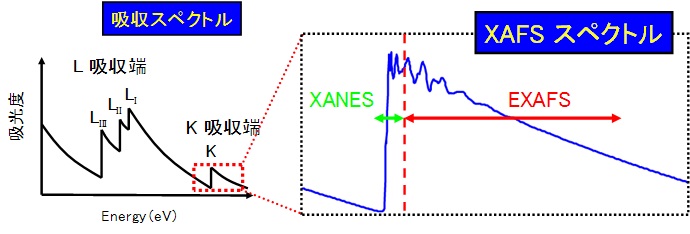
この微細な波々構造は吸収端付近では大きく、エネルギーが大きくなるに従ってだんだん小さく消えていってしまいます。X線吸収微細構造(XAFS)スペクトルは、波々ができる原因と含んでいる情報の違いから、さらに2つの領域に分けられます。
XANES[X線吸収端構造: x-ray absorption near edge structure]領域
EXAFS[X線広域微細構造: extended x-ray absorption fine structure]領域
なんだかアルファベットばかりで難しそうです。波々のでき方そのものを詳しく知ろうとすると量子力学だけでは不十分で、もっと難しい学問が必要となります(特にグリーン関数がいじれないと・・・)。高校で物理を取っていない私にとっては、理論的な深入りはできませんので、あしからず。
先に説明したように、XANES領域は、内殻軌道から空の電子軌道への遷移を見ているため、基本的に原子(原子核)の影響下にあります。X線のエネルギーを吸収して、電子が内殻軌道から空軌道へジャンプする時、そのスペクトルはローレンツ関数と呼ばれる釣り鐘状の吸収として現れます。この大きな吸収をwhite lineと呼び(昔は写真乾版で測定しており、強度の強いピークは真っ白に写ったためこう呼ばれるらしいです)、立ち上がりの吸光度が大きく変わる部分をabsorption edge(吸収端)と呼びます。吸収端の定義は明確ではありませんが、吸光度の増加が著しくなる点を選ぶことが多いです(吸光度の一次微分最大点)。
さらに、エネルギーがずっと高い空軌道(いわゆる連続帯)への吸収も、個々の吸収ピークの形はローレンツ関数で表されますが、そのピークの大きさはずっと小さく、互いに密接して吸収が起きます。その為、事実上どのようなX線のエネルギーを吸収しても自由に(連続帯へ)遷移できるようになり、その吸収はarctangent関数と呼ばれる崖の段差のようなスペクトルで表されます。X線のエネルギーがさらに高くなると、原子から電子が飛び出します(イオン化)。つまり、連続帯は空軌道への遷移と原子の外へ電子が飛び出す境界域になります。
連続帯の上限に近づくにつれ、吸収されるX線のエネルギーは、内殻(K核やL核)から電子をたたき出してイオン化するエネルギーに近づいていきます。そのため、連続帯の上限は常に一定の吸光度を示すようになります(平らなスペクトルになる)。ちなみに、連続帯の上限以上の余分なエネルギーは、電子が原子から飛び出していくエネルギーに使われます。これら全てを重ね合わせると、最終的にXANESスペクトルが得られます。
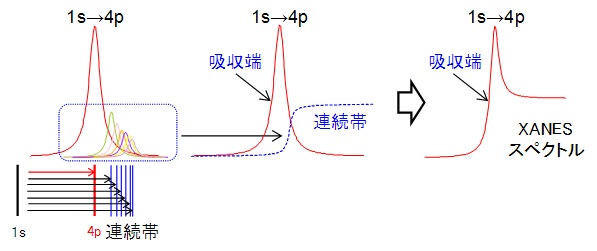
ちなみに、white lineと連続帯の区別も明確なものではなく、元素や化合物によって大きく異なります。連続帯の前に遷移可能な軌道が複数あれば、ピークは1つではなく複数現れます(下右図)。もっともこの場合でもwhite lineが一番大きなピークを示します。また、明瞭なwhite lineが無く、だらだらしたピークを持つ場合もあります(下左図)。我々が測定する物質は、元素が単独で存在している訳でなく、多くの元素の集合体でありかつ互いに結合し合ってできた化合物です。そのため、空軌道の状態はもはや単独の原子軌道ではなく、分子軌道を考えなくてはなりません。分子軌道は、結合する相手(配位子)の種類や配位子が対象元素の周りにどのように配置しているのかで大きく変わります。XANESスペクトルが価数や配位状態に敏感なのはこのためなのです。
例として、金属化合物の場合を見てみましょう。原子殻に近い内殻電子軌道はそれぞれの原子が持つ電子軌道とほぼ同じです。しかし、外側の電子軌道は隣の原子の電子軌道と重なり合い、伝導帯と呼ばれる軌道を形成します。ここを通じて電子が自由に動き回ります。金属が電気を通しやすい性質を持つのはこのお陰です。もし、この伝導帯がwhite lineとしての遷移先であれば(銅であれば4p軌道が重なり合ってできていたとすると)、伝導帯にはすでに電子が多く存在しますので、空軌道に比べ電子が励起する確率が減ってしまいます。その結果、white lineのピーク強度が弱くなり、だらだらした形状のスペクトルを与えることになります。
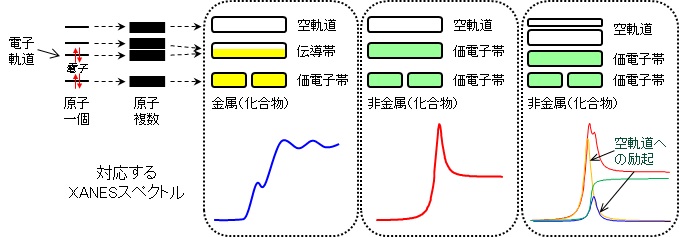
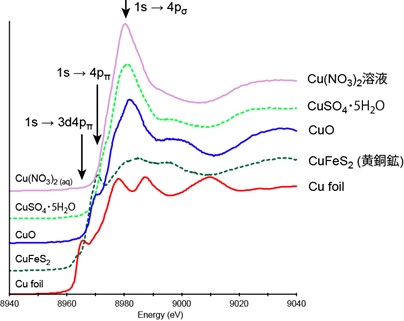
次に、銅の様々な化合物のXANESスペクトルの特徴を見てゆきましょう(下図)。金属や硫化物は明瞭なwhite lineを持たず、だらだら形状を示します。この理由は先に述べたとおりです。これに対し、酸化物、硫酸塩、水溶液のXANESスペクトルは、1つの大きなwhite lineを持ちます。さらに、酸化銅はwhite lineよりも前に、こぶ状のピークがあります。white line近傍に見られるこのようなこぶ状のピークを、shoulder peak(ショルダーピーク)と呼びます。
銅のXANESスペクトルは、X線のエネルギーを吸収して、電子が1s軌道から空軌道の4p軌道へジャンプする事で生じます。しかし、実際の化合物では、励起先に当たる4p軌道は、配位元素(酸素など)が持つ電子軌道と結びついてできた4pδ軌道・4pπ軌道といった分子軌道への遷移を見ることになります(例:小杉, 1989. 放射光, 2(4), 1-11.)。下の図では、酸化銅のwhite lineが1s軌道から4pδ軌道への遷移に、ショルダーピークが1s軌道から4pπ軌道への遷移に該当すると解釈されています。酸化銅に比べ、硫酸銅や硝酸銅水溶液は割とシャープなピークを持ち、かつ若干エネルギーが低い側にピークトップがあります。これは、硫酸銅や硝酸銅水溶液は酸化銅よりもイオン結合的で、配位子の酸素(両者共に水和水の酸素)の2p軌道と銅原子の4p軌道の重なりが小さくなるからだと考えられます。
第一遷移金属元素の場合、K吸収は電子がX線のエネルギーを吸収して、1s軌道から4p軌道へジャンプすることで起きます。4p軌道の内側には、エネルギーが低く電子の空きがある(電子が全て埋まっていない)3d軌道が存在します。しかし、選択則によって1s軌道から3d軌道への遷移は起きません。しかし、ある条件を満たすと、本来は起きないはずの1s軌道から3d軌道への遷移が起きます。その起きるはずのない遷移は、absorption edge(吸収端)よりも低いエネルギー位置に現れるため、pre-edge(プレエッジ)と呼ばれるます。詳しくは、山本孝(2007)X線分析の進歩.38,45-65.に非常に分かりやすい解説がされています。
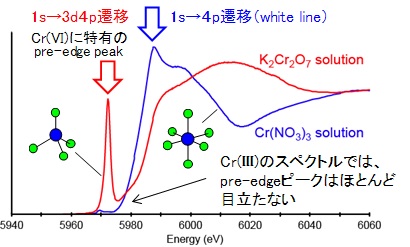
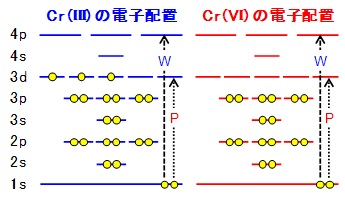
例として、Cr(NO3)3 水溶液とK2Cr2O7 水溶液のXANESスペクトルと(下左図)、Cr(III)とCr(IV)の電子配置と1s軌道電子の遷移先(下右図:W: white line, P: pre-edge peak)を示しました。Cr(NO3)3 水溶液のスペクトルには、明瞭なwhite lineに対してとても小さなプレエッジピークが見られます。一方、K2Cr2O7 水溶液のスペクトルには明瞭なwhite lineがありません。その代わりにより低いエネルギーの位置に、大きくシャープなプレエッジピークが見られます。この理由の1つは電子の密度です。3d軌道中の電子の数が、Cr(III)は3個であるのに対しCr(VI)は0個と、Cr(VI)の方が電子の空きが大きいため、遷移しやすくなります(下右図)。もう一つの理由は分子構造です。Cr(NO3)3 水溶液は第一遷移金属元素では一般的な6面体配位の構造を取るのに対し、K2Cr2O7 水溶液は四面体配位と大きく異なる分子構造を持ちます(固体の場合でも同様です)。この結果、K2Cr2O7 水溶液では、Crの3d軌道と4p軌道が交わることでdp混成軌道という新しい軌道を形成するため、Cr(III)の3d電子軌道に比べて電子が遷移しやすくなります。このプレエッジピークの強度を利用することで、物質中の元素の価数を求める事ができます。環境化学や地球化学の分野では大いに活用されています。
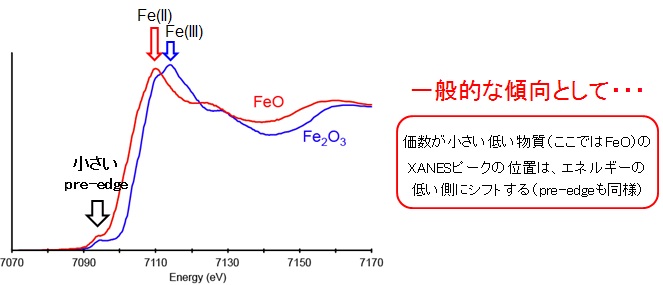
プレエッジピークがはっきり見られるのは、Ti(IV), V(V), Cr(VI), Mn(VII) などで、同じ第一遷移金属元素に属するFe(III), Co(II), Ni(II) Cu(II) のプレエッジピークはとても小さい事が分かっています。例として、FeO、Fe2O3 のXANESスペクトルを下に示してみました。Cr(VI) に比べると、プレエッジピークはとても小さいことが分かります。これは、2.1章で示した銅のXANESスペクトルでも同様です。山本(2007)によると、Ti(IV), V(V), Cr(VI), Mn(VII) の化合物は、3d軌道(正確にはdp混成軌道)が空の状態(電子の空きがたくさんある)であるため、比較的高い確率で電子が遷移でき、結果としてCr(VI) のXANESスペクトルのように大きなプレエッジピークを持つと考えられます(ビシバシ遷移できる)。一方、FeからCuまでの第一遷移金属元素は、すでに3d軌道に5個以上の電子が入っている状態で、そのdp混成軌道には電子の空きが圧倒的に少なくなってます。その結果、電子が遷移できる確率が低くなり(空きが少ない)、小さなプレエッジピークを示すと考えられます(山本,2007)。逆に言えば、XANESスペクトルのピーク強度は、電子軌道の混み具合の情報も保持していることが分かります。
ちなみに、一般的な傾向として、元素の価数が小さいほどXANESスペクトルのピークの位置はエネルギーの低い側へ、元素の価数が大きいほどXANESスペクトルのピークの位置はエネルギーの高い側へシフトすることが知られています。これを利用して、物質中の元素の価数を求める事もできます。特に、環境化学や地球化学の分野では、物質に微量に含まれる元素や鉱物などの小さな物質中の元素の価数の見積もりに活用されています(例:風送ダスト輸送途上における鉄の光還元反応の研究)。
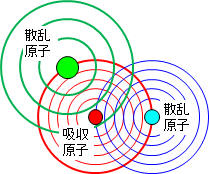
XANESとEXAFSの境界は吸収端から約50eVほどエネルギーが高い所です。ただ、厳密な境界ではありません。このエネルギーを超えると、電子は原子の束縛を離れて飛び出していきます(これを光電子と呼びます)。飛び出していった光電子の一部は、X線と同様に周辺の原子にぶつかって散乱されてあちこちへ飛び回ります。そのうち一部の散乱された光電子が飛び出した元の原子に再び戻ってきます。この出戻りの光電子と飛び出していく光電子の波が重なり合ったのが(電子は粒子でもあり波でもあります)、EXAFS振動となります。ちょうど、水面に石を投げた時に出来た波が、水面に顔を出している杭や岩に当たってはね返った波と重なり合って複雑な波模様を作り出すのと同じようなことが起きる訳です。実際には、光電子の波とX線が足し合わさったものを測定しています(検出器はX線と光電子の区別している訳でなく、その強度変化を黙々と測定している)。波の高さや模様から、周辺にある原子の種類や数を知ることが出来ます。
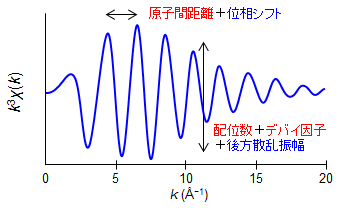
もう少し図を使って説明すると、X線の散乱による滑らかな変化(1)に、対象物質の密度・濃度に応じたX線の吸収によって生じるステップ状の変化(2)と、光電子同士が干渉した波(3)が重なり合ってXAFSスペクトルが出来ます。ちなみに、(2)のX線の吸収はXANES領域と光電子を生み出す過程を重ね合わせた効果です。我々が知りたいのは、対象とする物質中の原子の配置によって決まる光電子の波の重ね合わせです。この光電子の波を抽出するためには、バックグラウンドであるX線の散乱とX線の吸収スペクトルを差し引く必要があります。この説明を次の章でやりましょう。

補足説明:
ちなみに、XANESとEXAFSの境界となっている約50eVという数値は、X線によって原子(内殻軌道)からたたき出された光電子の波が、隣り合った原子の間(R)にちょうど1波長(λ)存在するエネルギーに相当します(つまり λ
= R)。光電子の波数(k)とエネルギー(E)の間には、E
= (hc/2π)k の関係式(h はプランク定数、c は光速)があります。ここで原子間距離(R)を2.5
Å(2.5 ×10−8 m)とした時、1波長(λ)がちょうどこの原子間距離に等しいとすると、k = 2π/λ の関係式から、E = hc/R
= 6.626×10−34 (J/s)
× 2.988×108 (m/s) / (2.5×10−8
(m) × 1.60218×10−19 (J/eV)) ≈ 50 eVとなります。XANES領域は原子と原子の間に、光電子の波長が一波長もない領域です。これに対して、EXAFS領域は、原子間に光電子の波がたくさんある領域になります。
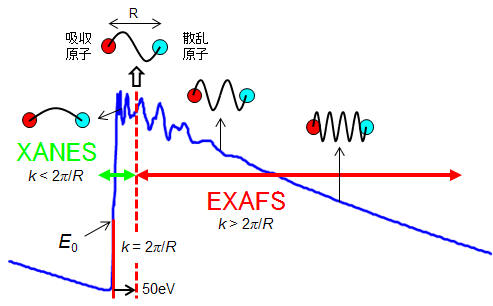
ここから少し専門的になっていきます。まず、測定したEXAFSスペクトルをμobs(E)と表すことにしましょう。吸収が起きる前の滑らかな変化が、吸収が起きた後の高エネルギー側の領域でもほぼ同じように続くと仮定します。このバックグランドの変化をμbk(E)と表す事にしましょう。バックグランドのX線吸収μbk(E)は、測定試料の材質(密度など)や測定機器によるX線の吸収など様々な効果が重なり合っていますが、実際には以前説明したようにX線の散乱による効果が主な原因です。そこで、X線散乱による強度変化を表す式(Victoreen(ビクトリーン)の式と呼ばれます)を用いて、吸収端(E0)の前のデータを近似することで、吸収端よりも高エネルギー側へ外挿します。
次に、原子が1つだけぽつんとあった時の仮想的な吸収スペクトル(μ0(E)と表します)、つまり飛び出していく光電子の波だけを推測して、これを実際のスペクトルからさっ引くことで、周辺の原子からはね返ってきた波を抽出します。干渉がないので滑らかなスペクトルになるはずです。もちろん、原子が1つだけのμ0(E)なんて測定できませんので、これもある仮定を導入して近似します。ただ、この近似スペクトルの推定が意外に難しく、EXAFS分析の誤差を生み出す原因にもなっています。多くの場合cubic spline法を用いて、実測スペクトル(μobs(E))の振動のちょうど中心を通るような滑らかな関数として近似します(ソフトウェアを使って最もらしいスペクトルを推定します)。
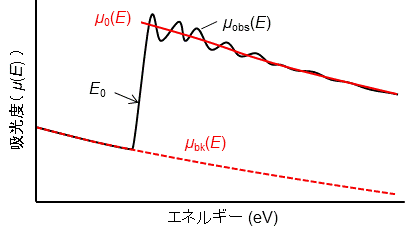
また、光電子の波の干渉がEXAFS振動になりますので、横軸は入射X線のエネルギーではなく飛び出した光電子の波数(k)つまり運動量に変換しておきます。吸収端(E0)を超えた時、たたき出された電子は、XANES領域では空軌道に収まりますが、EXAFS領域では光電子として原子を飛び出していきます。飛び出していく光電子の運動量を見積もるのに、基準点である吸収端(E0)を定義しておく必要があります。通常は、2.1章で述べたとおり、吸光度の増加が著しくなる点を選びます(μobs(E)の一次微分最大点)。吸収端(E0)を定義することで、光電子の運動量(k)を求める事が出来ます。例えば、E0から50 eV高いところではk = 3.6 Å−1、100 eV高いところではk = 5.1 Å−1、1000 eV高い所ではk = 16.2 Å−1となります。実際には、吸収端(E0)もパラメーターの一部としてフィッティングしますので、最初に厳密に決めていなくても大丈夫です。
最終的に、縦軸のEXAFSスペクトル(μobs(E))は、横軸をエネルギー(E)から光電子の運動量(k)に変更し、バックグラウンドであるX線の散乱と吸収を次の式で補正することで、EXAFS振動(χ(k))に変換されます(専門的になりますが、実際の解析ではさらにMcMuster(マクマスター)の吸収係数と同じになるように補正係数をかけます)。
χ(k) = (μobs(k) − μbk(k) − μ0(k))/μ0(k)
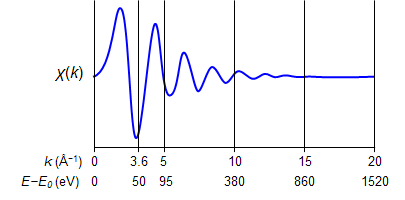
上の図が、測定スペクトルから得られたEXAFS振動(光電子の散乱スペクトル)になります。得られたEXAFS振動は、k の小さな領域(光電子のエネルギーが小さい領域)では振動が大きく目立つのですが、k の大きな領域(光電子のエネルギーが大きい)では振動が大きく減衰して目立ちません。そこで、k の大きな領域でも振動を大きくするために、EXAFS関数(χ(k))にkn(n = 2–3が良く用いられる)を掛けます。そうすると、下の図のように、k の大きな領域でもはっきりと振動が見えます。
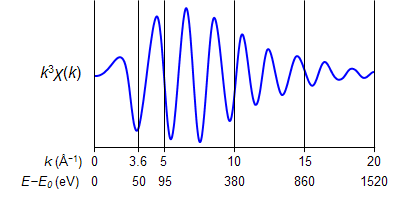
複雑な量子力学計算が必要なXANES領域と異なり、EXAFS振動はある近似を導入することで単純(?)な式で表すことが出来ます。詳細な導き方は参考書(宇田川康夫・日本分光学会測定法シリーズ26・X線吸収微細構造など)を見てもらうとして、ここでは、ごくごく非常に簡単に説明していきましょう。EXAFS振動(χ(k))は様々な干渉波から構成されます。そのうちの1つに着目してみましょう。すると、次のようになります。
EXAFS振動 χ(k) = 配位数 × 後方散乱振幅(散乱原子の種類)× 減衰率(デバイ・ワラー因子)× sin関数(原子間距離+位相のずれ)
赤字が実験スペクトルから得られる変数で、青字が理論計算で別に求めた値を代入する変数です。例えば、中心の原子Aから距離Rの位置にN個の原子Bがある場合、波の高さから配位数(N)と波の周期から原子間距離(R)を求める事が出来ます。配位数が増えるに従い振幅は大きくなり、原子間距離が増加するに従い波の周期は長くなります。
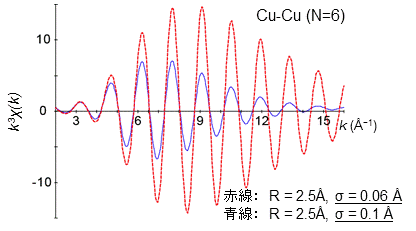
減衰率は光電子の運動量(k)とともに波の減衰する程度から求められ、デバイ・ワラー因子と呼ばれるもので表されます。このデバイ・ワラー因子は乱雑さを表すパラメーターです。例えば、ガラスは結晶に比べて構造が乱れているため、デバイ・ワラー因子が大きくなり、EXAFS振動がより大きく減衰します(静的な乱れと呼ばれます)。また、温度が高くなると原子が激しく振動するため、デバイ・ワラー因子が増加し、EXAFS振動が大きく減衰します(動的な乱れと呼ばれます)。例として、下の図を見てみましょう。中心にある銅原子から2.5 Åの距離に銅原子が6個分布し、そのデバイ因子が0.06 Åの時のEXAFS振動を赤色の点線で表してみました。このEXAFS振動に対して、デバイ・ワラー因子を0.1 Åと大きくした場合(青線)、その振動は光電子の運動量(k)とともに大きく減少してゆくことが分かります。縦軸の「配位数 × 減衰率」の値は割と正しく求まるですが、その内訳である配位数と減衰率それぞれを個別に正確に求める事はなかなか難しいです。
また、光電子を散乱する相手となる原子の種類が異なると、散乱されて戻ってくる光電子の波の高さと波の位置が異なってきます。これを表すのが、「後方散乱振幅(散乱されて戻ってくる光電子の波の高さ)」と「位相のずれ(波の位置がずれること)」です。難しい用語ですが、イメージとしてはバットでボールを打ち返すようなものです。ボール(光電子の波)が堅いバット(散乱原子)に当たるとすぐに強い波として戻ってきますが、柔らかいバット(散乱原子)だとブニョとへこむ分だけ波が戻るタイミングがずれて(位相のずれ)、フニャっと跳ね返されてるので、戻ってくる波が弱くなります(後方散乱振幅の変化)。また、あまりに早い速度でボールを投げられると(光電子のエネルギーが大きいと)、相手の原子によっては打ち返せなくなり、後方散乱振幅が小さくなったりします。
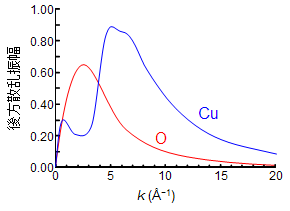
分かりやすく図に示してみましょう。下の図は、酸素と銅の後方散乱振幅が中心の銅から放出される光電子のエネルギーによって、どのように変化するのかを表しています。酸素は銅に比べてエネルギーの低い光電子(k = 2–4 Å−1)を強く散乱しますが(大きな波で戻ってくる)、光電子のエネルギーが高くなると散乱は急激に弱くなります(小さな波で戻ってくる)。一方、銅は酸素に比べエネルギーの高い光電子(k = 5–7 Å−1)を最も強く散乱するほか、k が大きい領域でも光電子を強く散乱できることが分かります(大きな波で戻ってくる)。
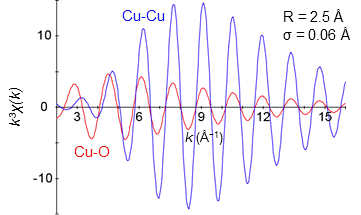
次に、中心にある銅原子から2.5 Å の距離に酸素または銅原子が6個分布している時、上の図で見た後方散乱振幅の変化がEXAFS振動としてどのような変化をするのか見ていきましょう。まず、散乱原子が銅の場合、k が 5–7 Å−1の範囲でEXFAS振幅が最大になるだけでなく、幅広いk の領域で振幅が常に大きい事が分かります。一方、酸素の場合、k が 2–4 Å−1の範囲で振幅が最大になりますが、銅に比べてEXAFS振動が非常に小さいことが分かります。水素、炭素なども酸素と同じように後方散乱振幅が小さいため、小さなEXAFS振動しか得られません。このため、これらの元素の位置情報の解析は、中心から近い時は可能ですが距離が離れるにつれて困難になります。一方、銅など大きな後方散乱振幅を持つ元素の配位情報は、中心から遠く離れても解析が可能ということです。
残念ながら、後方散乱振幅と位相のずれを、EXAFS振動(χ(k))の解析から配位数や原子間距離と同時に求める事は難しいため、実際の解析では、測定対象物質の構造や化学式が類似した物質から理論計算で求めた値を利用します。ワシントン大学のRehr教授が開発したFEFFと呼ばれる理論計算プログラムが広く用いられています(XANESの理論計算にも利用可!すごい)。構造や化学式がよく分からない時は、単純なモデルから計算されたMcKaleの表を用いて解析します(XAFS解析プログラムに予め入っている)。
![]()