Filtering
of Time Series of Feature Point Coordinates Using Non-Gaussian State
Space Model
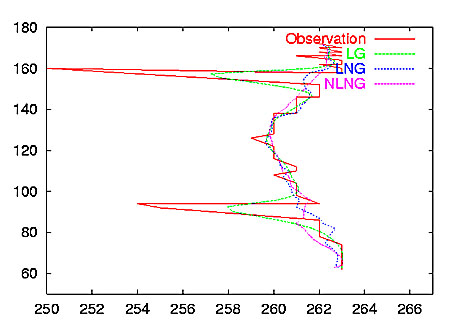
False matching due to error in feature extraction and change in illumination between frames may occur in feature point tracking on image sequence. The false matching leads to outliers in motion trajectories of feature points. We introduce a non-Gaussian state space model to reduce the effect of the outliers. Two models with heavy-tailed non-Gaussian observation noise distribution are used: linear non-Gaussian model with state vector which consists of coordinate of feature point and nonlinear non-Gaussian model with one which consists of both the coordinate and model parameters. In the latter model, online estimation of model parameters is carried out simultaneously in state estimation. A sequential Monte Carlo method is used to estimate the optimal state of these models. The experimental results using synthetic and real data show that the non-Gaussian models can reduce the effect of the outliers. In an example blow, red line represents observation, and green, blue and pink lines represent estimated trajectories by linear Gaussian model (LG) with Kalman filter, linear Non-Gaussian model (LNG) and nonlinear non-Gaussian model (NLNG). The effect of outliers were clearly reduced in the estimted trajectories of non-Gaussian state space model.
|
|
Stochastic
Filtering for Motion Trajectory in Image Sequences Using a Monte
Carlo Filter with Estimation of Hyper-Parameters
False matching due to errors in feature extraction and changes in illumination between frames may occur in feature tracking in image sequences. False matching leads to outliers in feature motion trajectory. One way of reducing the effect of outliers is stochastic filtering using a state space model for motion trajectory. Hyper-parameters in the state space model, e.g., variances of noise distributions, must be determined appropriately to control tracking motion and outlier rejection properly. Likelihood can be used to estimate hyper-parameters, but it is difficult to apply online tracking due to computational cost. To estimate hyper-parameters online, we include hyper-parameters in state vector and estimate feature coordinates and hyper-parameters simultaneously. A Monte Carlo filter is used in state estimation, because adding hyper-parameters to state vector makes state space model nonlinear. Experimental results using synthetic and real data show that the proposed method can estimate appropriate hyper-parameters for tracking motion and reducing the effect of outliers.
The figures blow show the snapshots of the eye tracking image sequence. The arc in pictures shows the estimated eye position obtained from the filter based on the self-organizing model. Graphs show changes in velocity, the system noise hyper-parameter, and the observation noise hyper-parameter. Hyper-parameters were properly varied based on changes in velocity: large scale parameter of system noise distribution were used for large velocities and small ones selected for the small velocities.
|
|
(MPEG 4.2MB)