AIスピニング加工技術
- 機械学習を用いた絞りスピニングにおける板厚制御 -
1.はじめに
スピニング加工は回転する板材や管材をローラ工具で押して変形させ,所望の形状に成形する塑性加工法である[1],[2].プレス加工と比べて金型コストが低く試作や多種少量生産にも有利である.局所的な変形のため加工力が小さく製品寸法に比して装置の規模が低く抑えられる.ニアネットシェイプ加工であって材料の節約につながる.自動車部品,宇宙航空部品,化学産業,食品産業,空調機器,圧力容器,調理器具などに広く用いられている.
板材からの成形では目標形状のマンドレルにワークを押し付けて同じ形状を得る.板材のスピニングは複数のローラパスに沿ってワークを段階的に変形させる絞りスピニング(Fig.1 (a))と,金型側面に沿った単一のパスでローラを動かすしごきスピニング(Fig.1 (b))に大別される.本資料では前者を取り上げる.
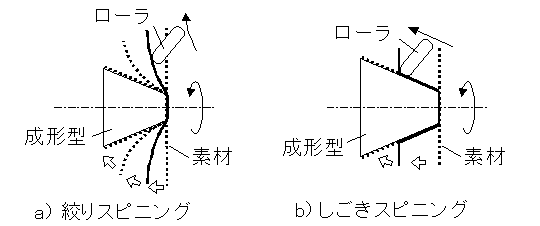
Fig.1 スピニング加工
しごきスピニングの成形品の板厚 t は,ブランク板厚を t_0 ,円錐半角を θ とすると一定値 t_0 sin θ となる(sine則).それに対して絞りスピニングの成形品の板厚分布はローラパスに依存して変化し,薄肉化を防ぐことができるという利点を有する.一方,パスによってはワークにしわや破断が生じ成形に失敗する場合がある.目標の板厚分布を得る一般的なローラパスの設計法は確立していない.生産現場ではジョイスティックにより作業者が手動でローラを制御する教示再生式のスピニングマシンが用いられ,作業者の経験と試行錯誤によりローラパスを作成する場合が多い.熟練作業者による手動のローラパスを記録し,ローラパス設計のルールを抽出する研究も見られる[3].
絞りスピニングに関する従来研究としては,有限要素法(FEM)による成形シミュレーションにより,ローラ下の応力や歪みなどの変形メカニズムや,加工条件が成形品に及ぼす影響の解明が試みられてきた[4],[5],[6],[7].加工パスの形状としてインボリュート曲線[8],楕円弧の一部[9],2次ベジエ曲線[10]などが用いられ,加工パラメータと板厚の関係や,しわや破断の発生が研究されている.また絞りスピニングのプロセス全体を対象として,加工パラメータの加工結果への影響の統計的解析が行われた[11].さらにプロセス全体の計画方法として,事例ベース推論とファジィモデルを用いて欠陥発生を回避する統計的手法が提案されている[12].また近年スピニング加工においても機械学習の応用が見られ,フローフォーミングにおける表面損傷の予測[13]やボールスピニングにおける形状予測[14]に人工ニューラルネットワーク(ANN)が用いられた.
本資料では,機械学習を用いた絞りスピニングによる板厚の制御方法を紹介する[15],[16].FEMなどに基づく従来の研究ではパスと板厚の関係について定性的な傾向を指摘するにとどまっていたが,本手法では円筒カップの複数の点の目標板厚を同時に実現できる.ローラパスをパスの往復回数,寸法,形状などの複数のパラメータで表現する.それらのパスパラメータと成形品の板厚分布の関係をANNで学習し,板厚分布をパスパラメータの関数として表す加工プロセスの予測モデルを作成する.板厚分布に目標値を設定し,数値解法によりパスパラメータを逆算して,希望する板厚分布を実現するローラパスを求める.得られたパスパラメータを用いて実際に円筒カップの成形を行い,目標の要求仕様を満たす絞りスピニングの加工プロセスが実現できることを確かめる.
2.ローラパス生成システム
多サイクルの絞りスピニングによる円筒カップ形状の成形において,ローラパスを自動的に生成するシステムを構築する.加工プロセスには,マンドレルで決定される目標形状以外に,成形品の高さや板厚などの製品仕様が定められている.複数の要求事項が与えられた時,それらを同時に満足するローラパスを,数理的な手段を用いて直接的に求める.そのためには以下の4つのステップが必要である.
① スピニングにおける多サイクルのローラパスを複数のパスパラメータで表現する.パスパラメータとしては,パス回数,パス寸法,ローラフィード比や,パスの形状を表わす様々な数値などがある.これらをベクトル
p=(p_1, p_2,..., p_n) (1)
で表わす.
② 加工プロセスの結果を複数の特性値で表現する.成形品の特性値としては高さ,板厚,スプリングバック,表面粗さなどが考えられる.これらは製品に要求される設計仕様として与えられる.これらをベクトル
q=(q_1, q_2,..., q_m) (2)
で表わす.ただしn≧mとする.
③ パスパラメータ p と特性値 q の関係を多変数ベクトル関数で表現する.スピニングにおいて安定に加工可能な範囲では加工プロセスに再現性があり,同じパスに対する加工結果は等しいと認められる.確率的要素の入らない決定論的なプロセスなので,パスパラメータ p を与えれば特性値 q は一意に決まる.したがって,多変数ベクトル関数 f を用いて加工プロセスを
q=f(p) (3)
と表わせる.関数 f は実験やFEMによるシミュレーションなどから導出することができる.本手法では実験結果をANNに学習させることにより関数 f を推定する.
④ 成形品の特性値に設計仕様で決められた目標値 q_d を代入し,望ましい加工プロセスを方程式
q_d=f(p) (4)
と表わす.プロセス方程式(4)を未知の p に関して逆問題として解くことにより,成形品の設計仕様を満たすパスパラメータ p が決まり,工具パスが得られる.関数 f は一般に解析的には表わされないため,本資料では反復解法により数値的に式(4)の解を求める.
2.1 ローラパスのパラメータ表現
多サイクルの絞りスピニングでは,ローラがマンドレルとワーク外周の間を往復しながら,ワーク形状を平板のブランクから円筒形状まで徐々に変化させる.ローラが通過するすべての座標値を加工結果と関連付けることは不可能なので,加工開始から加工終了までの1セットのローラパスをいくつかのパラメータで表現する.パラメータから生成されるローラパスは,しわや破断などの欠陥なく成形可能なパスを含むだけでなく,成形可能な範囲内で十分多様な特性の成形品が成形できる自由度を持たなくてはならない.
ローラパスは成形品に沿う直線パスとマンドレルにワークが接しない曲線パスから構成される.曲線パスは成形品側面からワーク外周に向かう一方向のパスとした.曲線パスの形状は,外周に近づくほど主軸に対する傾斜角が大きくなる下に凸の形状である.このタイプの曲線パスは,しわが発生しにくくワークを安定に変形できるため,生産現場や多くの研究で採用される.一つの曲線パスが終了するとローラはワークに触れずに曲線パスの始点に戻って次の直線パスに接続する.曲線パスは単位円弧をx方向(軸方向),y方向(半径方向)に伸縮した下に凸の楕円弧である(Fig.2).
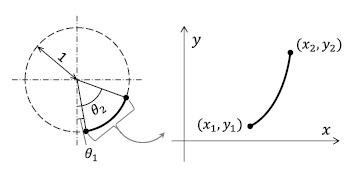
Fig.2 曲線パスの生成
ローラパスを表わすパラメータは以下のように構成される.n_pはパス往復回数である.座標系の原点は,ブランク面のx座標x_p0,成形品側面のy座標y_p0をそれぞれゼロとおき,これを原点とする.各曲線パスの始点は成形品側面に沿ってx方向に一定間隔Δx_pで前進する.曲線パスの始点と終点を結ぶ傾斜角αは初期値α_0から一定角ずつ増加し,最終パスで α=π/2 となって成形品側面に沿う.kパス目の傾斜角αは α=α_0+(π/2-α_0 )(k-1)/(n_p-1) となる.原点からスタートした最初の直線パスが外周に向かう最初の曲線パスに切り替わる点を (x_p_start,0) とする.各曲線パスの終点は(x_p_start,0)を中心とし(x_p_start,y_p_end)と(x_p_end,0)を通る1/4楕円上にある.x_p_endはローラパスの終了位置のx座標である(Fig.3).
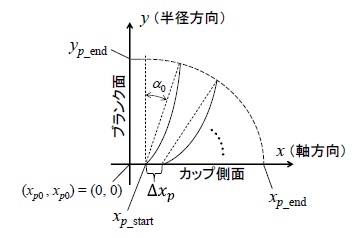
Fig.3 パスパラメータの構成
ローラパスの形状と寸法を規定するこれらのパラメータのうちで n_p,x_p_start,x_p_end,y_p_end,Δx_p,α_0の6つを可変パラメータとする.これにパスに沿った1回転当たりのローラフィード比 P_feed を加えて,合わせて7つを式(1)のパスパラメータ p の要素とした.
2.2 加工パラメータと特性値の関係の予測モデル
本システムでは実験結果をANNに学習させることによりパスパラメータ p と特性値 q の関係 q=f(p) を推定する.一方,FEMシミュレーションによりパスパラメータ p から特性値 q を求めることも理論的には可能である.しかし後でプロセス方程式(4)を反復解法により解く段階で,関数 f の計算を非常に多くの回数行う必要がある.そのため時間およびコストのかかるFEMの計算を反復解法に用いることは実用的ではない.学習終了後のANNは計算が非常に早く,反復計算への使用に有利である.実験の代わりにFEMを用いるとしても,FEMの計算結果を予めANNに学習させる方法が有益であろう.
ここではANNとして任意の非線形関数を近似可能な多層パーセプトロン(MLP)を用いる.MLPの入力がパスパラメータ p ,出力が特性値 q に相当する.MLPはそれぞれ複数のノードからなる入力層,隠れ層,出力層からなる.隠れ層と出力層の各ノードは前の層の各ノードから入力を受け取り,その重み付き和の非線形関数を出力する.この関数を活性化関数と呼ぶ.ここではシグモイド関数を用いた.
MLPの教師付き学習では,入力 p と出力 q の組合せからなる複数の訓練データに基づいてノード間の重み係数を調整する.すなわち訓練データの各サンプル入力 p をANNに与えたときの出力が, p に対応する訓練データのサンプル出力 q に収束するように重み調整の反復計算を行う.学習アルゴリズムとしてMLPの教師付き学習に広く用いられるバックプロパゲーションを採用した.
2.3 反復計算によるプロセス方程式の数値解
最後に,設計仕様で定められた目標値 q_d を代入した方程式 (4) を数値的に解く.関数 f(p) の p に関するヤコビ行列を
J(p)=∂q/∂p=(∂f(p))/∂p (6)
とする.行列 J の要素 J_jk は, p の要素 p_k の微小変化をεとして,数値微分により
J_jk=(∂f_j (p))/∂p_k≒(f_j (p_1,...,p_k+ε,...,p_n )-f_j (p_1,...,p_k-ε,...,p_n ))/2ε (7)
で近似計算できる.
パスパラメータ p の現在値 p_c によりANNから出力される値 f(p_c) と目標値 q_d の偏差 e を
e=f(p_c)-q_d (8)
とする.パスパラメータ p の修正則として計算が簡単な最急降下法を用い,転置ヤコビ行列 J^T を用いてパスパラメータ p の修正ベクトルΔp を計算した.
Δp =-αJ^T e (αは係数) (9)
転置ヤコビ行列 J^T を構成する列ベクトルは p の各要素の勾配が最大となる方向を示す.したがって Δp は偏差 e の各要素を最もゼロに近づける方向の p の変化を各要素の値で重み付けして合成したベクトルになる.この Δp を用いてパスパラメータの現在値を
p_c→p_c+Δp (10)
と更新する.
(6)~(10)の計算を q_d≒f(p) となるまで繰り返すことにより,目標値 q_d を実現すると推定されるパラメータ p が求められる.Fig.4に上記アルゴリズムのフローチャートを示す.p の要素がn個の場合,反復ごとに2n+1回の関数 f(p) の計算が必要であり,ANNの計算の高速性が役に立つ.
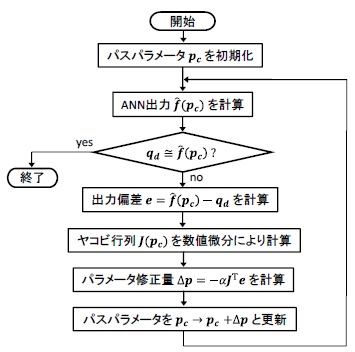
Fig.4 パスパラメータの数値解法
この方法で,理論的には最大でパスパラメータの個数と同じ個数の特性値を同時に目標値に一致させることができる.特性値の個数がパスパラメータの個数より少ない場合,パスパラメータは冗長となり,特性値を満たすパスパラメータの組合せは無数に存在する.提案するアルゴリズムはそのうちの一つの解に収束する.
3.実 験
ブランクは直径150mm,板厚1.49mmのアルミニウム(A1050-O)円板とする.中央に直径20mmの固定用の穴が開けてある.直径85mm,高さ90mmの円柱形状のマンドレル(S45C焼入)を用いた.ローラは工具鋼(SKD11焼入)で,直径70mm,丸みR8mmである.マンドレル軸に対して45°傾斜したローラホルダにローラを装着する.加工機として定格推力1kNのリニアモータ駆動スピニング加工機17)を用いた.マンドレルの回転速度は180rpmである.Fig.5に実験装置を示す.

Fig.5 実験装置
成形品の特性値 q として,側面の板厚,高さh,余剰パス長 r_p を取り上げた.板厚は底面からの高さ25%,50%,75%の3か所の板厚 t_(25%),t_(50%),t_(75%) である.高さはハイトゲージ,板厚はマイクロメータで測定した.また余剰パス長 r_p は最後の直線パスにおいてローラが成形品の後端を通り過ぎる距離を意味し,次式で定義される.
r_p=x_p_end-(h+R_round) (11)
ただし R_round はローラの丸み半径である.数値制御による絞りスピニングにおいて,各パスの終端位置は必ずしもワークの後端とは一致しない.r_p が正の大きな値でパスがワーク後端を大きく通り過ぎる場合,成形に寄与しない無駄な時間が増加する.一方,r_p が負でパスがワークの後端に達しない場合,ワーク外周にフランジが形成され,薄肉化や破断が発生する恐れがある.したがって r_p は0付近となることが望ましい.
ANNおよび数値解法はC言語でプログラムした.ANNの入力層のノードは7個である.隠れ層は1層で7個のノードからなる.5個の出力に対してそれぞれ独立のANNを構築した.バックプロパゲーション法によるANN学習の反復回数は5000回に固定した.またANNによる推定性能を高めるため,ブースティング法によるアンサンブル学習を採用し,並行して学習した10個のANNの出力を合成して推定値を計算した.
3.1 ANNによる特性値の推定
はじめに,ANNにより板厚などの特性値が推定可能なことを検証した.予測モデルの関数 f(p) を構築するために,成形実験により取得したデータ群AをANNに学習させた.データ群Aは18組の入力(7個のパスパラメータ)と出力(5個の特性値)からなる.パスパラメータをパラメータ空間内で適度に配分するため,実験計画法のL18直交表を部分的に乱数化したパラメータ値を用いた.パラメータの範囲は13<n_p<26,0<x_p_start<8 [mm],57.9<x_p_end<97.8 [mm],24<y_p_end<34 [mm],0<Δx_p<(x_p_end-x_p_start)/n_p,0<α_0<20 [°], 0.8<P_feed<2.4 [mm] とした.
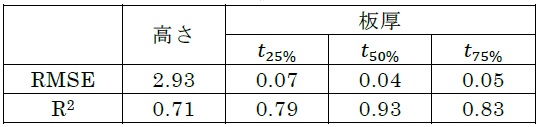
また検証用のデータ群Bを成形実験により取得した.上記と同じ範囲内の一様乱数により18回分の加工のパスパラメータを計算し,破断が生じた1回を除く17組のデータ群Bにより予測モデルを検証した.Fig.6では,(a)高さh と板厚(b)t_(25%),(c)t_(50%),(d)t_(75%) について,データ群BのパスパラメータをANNに入力して得られた推定値と成形実験における実測値を比較している.各グラフの横軸が推定値,縦軸が実測値である.また推定値の実測値に対する二乗平均平方根誤差(RMSE)および決定係数(R2)を計算した(Table 1).ANNによる推定値は実測値とよく一致しており,パスパラメータと成形品の特性値の関係はANNによって適切にモデル化されている.
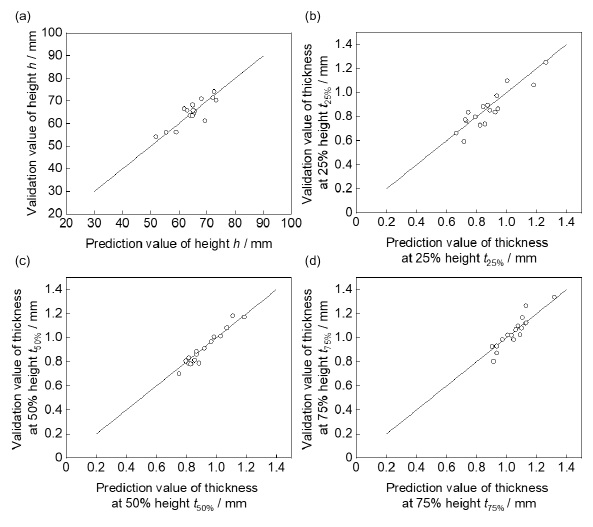
Fig.6 ANNによる推定値と実測値の比較
Table 1 ANN 推定値の RMSE および R^2
3.2 数値解法による特性値の制御
次に,板厚などの特性値に目標値を設定し,2.3節の数値解法により目標値を実現するパスパラメータを求める.ANNの推定精度を向上させるために前節のデータ群A,Bを合わせた35組のデータをANNに学習させた.目標板厚は3か所の板厚が一定(t_(25%)=t_(50%)=t_(75%))となるように与え,0.6mmから1.2mmまで0.1mmおきに7通りの板厚とした.円筒側面が一定の板厚で目標板厚となるカップの高さを計算し,これを目標高さとした.また式(11)の余剰パス長 r_p は目標値を0とした.パスパラメータの初期値は学習データのパラメータを用いた.式(6)~(10)の反復計算によりパスパラメータを求めたところ,板厚0.6,0.7mmでは解が収束しなかった.目標板厚0.8~1.2mmの範囲で22組のパスパラメータを選び,成形実験を行った.同じ目標板厚に対しても異なる初期値からは異なるパスパラメータに収束するため,同一の目標値に複数のパスパラメータが対応している.
Fig.7は,(a)高さh と板厚(b)t_(25%),(c)t_(50%),(d)t_(75%) に関して,数値解法の目標値と成形実験における実測値を比較する.各グラフの横軸が目標値,縦軸が実測値である.目標板厚1.2mmで目標値からやや外れるケースが見られるが,おおむね目標値に近い板厚や高さとなっている.Table 2 は成形品の実測値の目標値に対するRMSEを示す.最大0.1mm以内のRMSEで板厚制御が実現できている.Fig.8 にローラパスとそれによる成形品の断面の例を示す.a)b)は学習データ,c)は板厚制御の結果である.a)b)の断面では板厚t_(50%)がt_(25%),t_(75%)よりも薄肉化し,高さ方向の板厚の変動が顕著である.一方c)の断面では t_(25%),t_(50%),t_(75%) がほぼ等しくなるように成形されている.
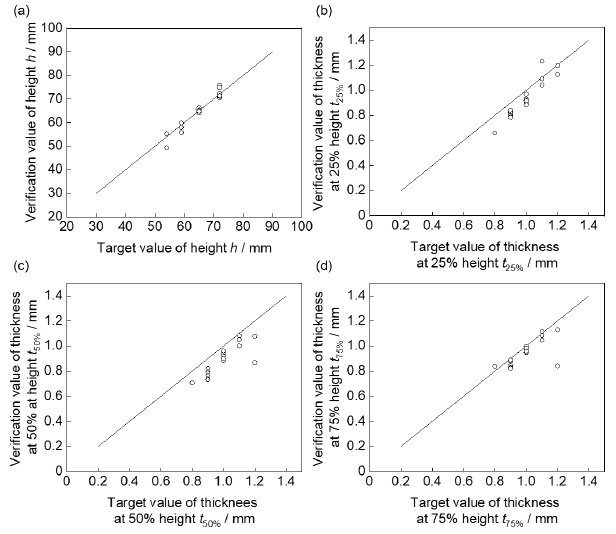
Fig.7 板厚・高さ制御における目標値と実測値の比較
Table 2 成形品の実測値の目標値に対する RMSE

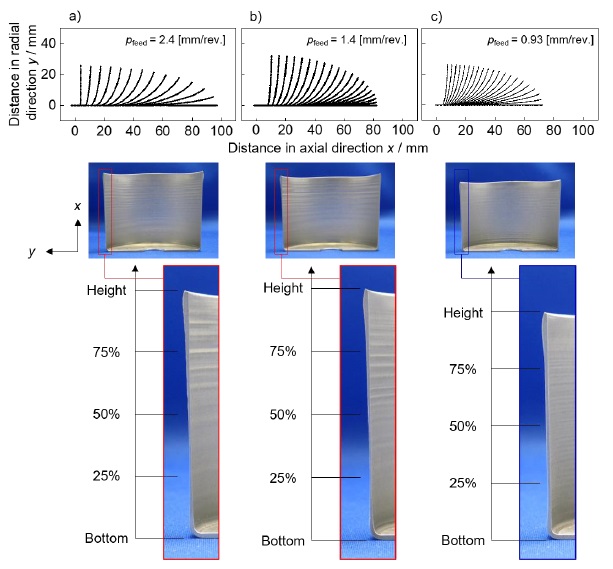
Fig.8 ローラパスと成形品断面の例 a)b)学習データ c)板厚制御の結果
4.ブランク・マンドレルの寸法変動への対応
ここまではブランクおよびマンドレルの寸法を1種類の組合せのみとした.しかし実際の現場では同じ円筒カップ形状でも様々な寸法のブランクとマンドレルの組合せで成形を行うことが必要となる.その際に,寸法ごとに独立にANNの学習を行うのではなく,既に蓄積された別の寸法の学習データを有効に利用できれば効率的である.すなわち未学習のブランク・マンドレル寸法に対して,異なる寸法のブランク・マンドレルによる学習結果に基づいて,成形結果の予測や制御が可能となることが望ましい.
上記のような拡張を行うため,ANNに入力する式(1)のパラメータに対して,加工ごとに可変となるパスパラメータのほかに固定的な加工条件に相当するパラメータを追加する.ブランクおよびマンドレルの寸法はこうしたパラメータとして扱うことができる.寸法パラメータ+パスパラメータの組合せでANNの学習を行い,未知の寸法パラメータ+パスパラメータをANNに入力することで成形結果が予測できる.
ブランク直径D,マンドレル直径dとして (D,d) = (90,50),(110,50),(130,85),(150,85)の組合せについて8回ずつ成形実験を行い,結果をANNに学習させた.これらの組合せには含まれない(D,d)= (120,70),(140,70)についてANNによる推定値と実測値を比較した(Fig.9).グラフは板厚t_(50%)のブランク板厚に対する比率を表わす.またプロットのうち一点についてt_(25%),t_(50%),t_(75%)の比較を示した.いずれも推定値と実測値の一致は良好であり,未学習の寸法でも成形結果の予測は可能である.
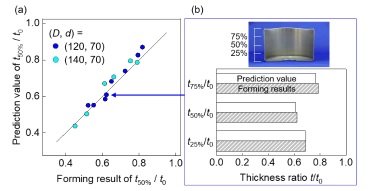
Fig.9 未学習のブランク・マンドレル寸法に対する板厚推定
一方,板厚や高さの制御においては,ブランク・マンドレルの寸法は一定値に固定し,可変のパスパラメータのみを変動させて目標の特性値を実現するパラメータを求めることが必要である.そのためには式(7)のヤコビ行列をパスパラメータのみに関して特性値を偏微分した部分ヤコビ行列に置き換えればよい.複数の寸法組合せの学習データで板厚を制御した結果をFig.10に示す.やや目標値から外れる場合も見られるが,おおむね目標値通りの板厚が実現されている.
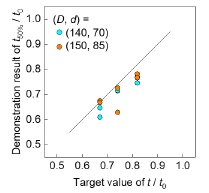
Fig.10 寸法混合のブランク・マンドレルによる学習データに基づく板厚制御
5.おわりに
機械学習を用いた絞りスピニングによる成形品の特性値の制御方法を紹介した.円筒カップの多サイクル絞りスピニングにおいて,ローラパスのパラメータと加工結果の特性値データをANNで学習し,複数の出力目標値を実現するパスパラメータを数値解法により求めるシステムを構築した.得られたパスパラメータで成形品の複数個所の目標板厚が同時に達成できることを実験的に検証した.
関連論文(ダウンロード可)
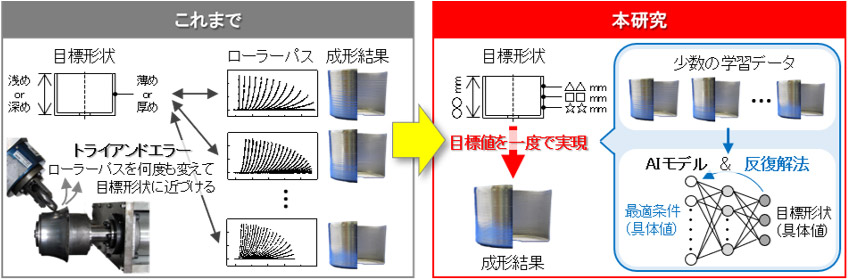
・少数データから短時間で現場環境に応じた最適加工条件を決定 -素形材産業における小規模製造現場のDXに貢献する作業支援汎用AIツール-
(PDF)
リンク
スピニング加工・へら絞り リンク集
研究テーマへ戻る
荒井のページへ戻る