The dining mathematicians are a classical mutual exclusion problem: There are two mathematicians living at the same place, whose life is focused on two activities, namely thinking (TH0 and TH1, respectively) and eating (EAT0 and EAT1, respectively), see Fig.1. As they have a strong disliking for each other, they never want to eat at the same time. To ensure this, they agreed to the following protocol. They both have access to a common variable (VAR n) storing integer values. If the stored integer (n) is even, the first mathematician is allowed to start eating. When finished, the first mathematician sets the stored value to (n/2). A similar procedure holds for the second mathematician, where the check is if the value of the stored variable is odd, and the value written back after eating is (3n+1).
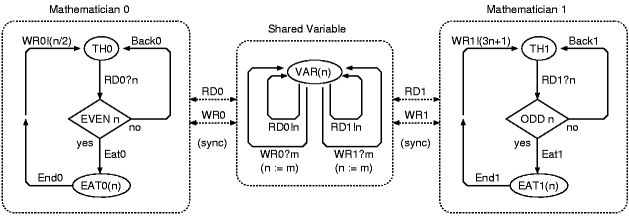
Fig.1. the Dining Mathematicians.
The dining mathematicians are a
classical mutual exclusion problem: There are two mathematicians living
at the same place, whose life is focused on two activities, namely
thinking (TH0 and TH1, respectively) and eating (EAT0 and EAT1,
respectively), see Fig.1. As they have a
strong disliking for each other, they never want to eat at the same
time. To ensure this, they agreed to the following protocol. They both
have access to a common variable (VAR n) storing integer values. If the
stored integer (n) is even, the first mathematician is allowed to start
eating. When finished, the first mathematician sets the stored value to
(n/2). A similar procedure holds for the second mathematician, where
the check is if the value of the stored variable is odd, and the value
written back after eating is (3n+1).
Fig.2 shows this implementation described in CSP-Prover. Here, each of the process definitions (EAT0 n), (EAT1 n), and (VAR n) describes infinitely many equations. The question is: does this now precisely described implementation exclude the situation where both mathematicians eat together? Or, on a more formal level: has this implementation a trace where Eat1 appears between consecutive communications Eat0 and End0 (and vice versa)?
- datatype Event = Eat0 | Back0 | End0 | RD0 int | WR0
int
-
| Eat1 | Back1 | End1 | RD1 int | WR1 int
- | NUM int
- syntax
-
"_CH0" :: "Event set" ("CH0")
-
"_CH1" :: "Event set" ("CH1")
-
"_OBS" :: "Event set" ("OBS")
- translations
-
"CH0" == "(range RD0) Un (range WR0)"
-
"CH1" == "(range RD1) Un (range WR1)"
- "OBS" == "{Eat0, Back0, End0, Eat1, Back1, End1}"
- defs
FPmode_def [simp]: "FPmode == CMSmode"
- datatype
ImpName = VAR int | TH0 | EAT0 int | TH1 | EAT1 int
- consts
-
Impfun :: "ImpName => (ImpName, Event) proc"
- primrec
-
"Impfun (TH0) = RD0 ? n -> IF (EVEN n)
-
THEN Eat0 -> $(EAT0 n)
-
ELSE Back0 -> $(TH0)"
-
"Impfun (TH1) = RD1 ? n -> IF (ODD n)
-
THEN Eat1 -> $(EAT1 n)
-
ELSE Back1 -> $(TH1)"
-
"Impfun (EAT0 n) = End0 -> WR0 ! (n div 2) -> $(TH0)"
-
"Impfun (EAT1 n) = End1 -> WR1 ! (3 * n + 1) -> $(TH1)"
-
"Impfun (VAR n) = WR0 ? n -> $(VAR n)
-
[+] WR1 ? n -> $(VAR n)
-
[+] RD0 ! n -> $(VAR n)
-
[+] RD1 ! n -> $(VAR n)"
- defs
(overloaded)
-
Set_Impfun_def [simp]: "PNfun == Impfun"
- consts
-
Imp :: "int => (ImpName, Event) proc"
- defs
- Imp_def: "Imp == (%n. ($TH0 |[CH0]| $(VAR n) |[CH1]| $TH1) -- (CH0 Un CH1))"
Fig.2. The dining mathematicians:
CSP-Prover description of the concrete implementation
The classical argument in analysing this implementation is to provide an abstraction of the dining mathematicians, which clearly has the desired exclusion property. Fig.3 shows such a specification described in CSP-Prover: it consists only of three states, which stand for the situations `both mathematicians think' TH0_TH1 and `one mathematician eats while the other is thinking' (EAT0_TH1 and TH0_EAT1, respectively). The CSP operator ! x:X -> P(x) makes an (internal) choice between the events of X and then proceeds with the process P which can depend on the chosen value of x. Starting in state TH0_TH1 with an observation Eat0, the event Eat1 is excluded from the possible communications till an End0 appears (and vice versa for Eat1, Eat0, and End1).
- datatype SpcName = TH0_TH1 | EAT0_TH1 | TH0_EAT1
- consts
-
Spcfun :: "SpcName => (SpcName, Event) proc"
- primrec
-
"Spcfun
-
(TH0_TH1) = ! x:OBS -> IF (x = Eat0) THEN ($EAT0_TH1)
-
ELSE IF (x = Eat1) THEN ($TH0_EAT1)
-
ELSE ($TH0_TH1)"
-
"Spcfun
-
(EAT0_TH1) = ! x:(OBS - {Eat1}) -> IF (x = End0)
-
THEN ($TH0_TH1)
-
ELSE ($EAT0_TH1)"
-
"Spcfun
-
(TH0_EAT1) = ! x:(OBS - {Eat0}) -> IF (x = End1)
-
THEN ($TH0_TH1)
-
ELSE ($TH0_EAT1)"
- defs
(overloaded)
-
Set_Spcfun_def [simp]: "PNfun == Spcfun"
- consts
-
Spc :: "(SpcName,Event) proc"
- defs
- Spc_def: "Spc == $TH0_TH1"
Fig.3. The dining mathematicians:
CSP-Prover description of the specification
With CSP-Prover we can show that (Imp n) is a stable-failures refinement of Spc for any integer n, thus `ALL n. Spc <=F Imp n'. As Spc is a sequential process, this refinement result also establishes deadlock-freedom of (Imp n). The theory files for this proof are given as follows:
DM1_Imp_def.thy : defines Imp
DM2_para.thy : expands parallel operators in Imp
DM3_hide.thy : expands hiding operators in Imp
DM4_Spc_def.thy : defines Spc
DM5_Spc_Imp.thy : proves Spc <=F Imp
References
[Clarke2001] E. M. Clarke and H. Schlingloff. Handbook of Automated Reasoning. Elsevier Science, 2001.