Uniform Candy Distribution Puzzle

AIST and Swansea University

Unifrom Candy Distribution Puzzle

This is a classical example of self-organizing systems as follows:

• Uniform Candy Distribution Puzzle: k children are sitting in a circle. Each child starts out with an even number of candies. The following step is repeated indefinitely: every child passes half of her candies to the child on her left; any child who ends up with an odd number of candies is given another candy by the teacher.
  Prove: Eventually all children will have the same amount of candy.

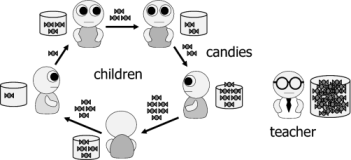
For example, see "The Puzzle TOAD". We proved this puzzle by CSP-Prover when children asynchronously pass their candies. This is the first prototype for proving the puzzle, and it will be reorganized and improved later.

You can prove the puzzle as follows:

1. Download the package of theory files for extending CSP-Prover version 4.0:
   
   
   • CSP_F_v4_1.tar.gz for Isabelle 2005  (README, dependency-graph)
     
   • CSP_F_v4_1_2008.tar.gz for Isabelle 2008
     
   
   because this puzzle needs an extended CSP-Prover-4-0 with the package "CSP_F_v4_1". This is a test version of the developing CSP-Prover-4-1.
   
   
2. Unpack it and make the heap file "CSP_F_v4_1" as follows:
   
   
   • For Isabelle 2005,
     (1) tar zxvf CSP_F_v4_1.tar.gz
     (2) cd CSP_F_v4_1
     (3) isatool usedir -b CSP_F CSP_F_v4_1
         (It requires the heap file "CSP_F" of CSP-Prover-4-0. see here).
     
     
   • For Isabelle 2008,
     (1) tar zxvf CSP_F_v4_1_2008.tar.gz
     (2) cd CSP_F_v4_1
     (3) isatool usedir -b CSP_F CSP_F_v4_1
         (It requires the heap file "CSP_F" of CSP-Prover-4-0-Isabelle-2008. see here).
     
   
   
3. Download the package of theory files of Uniform Candy Distribution Puzzle:
   
   
   • Uniform_Candy_Distribution_02.tar.gz for Isabelle 2005  (README)  (15 May 2008
   • Uniform_Candy_Distribution_2008.tar.gz for Isabelle 2008  (README)  (03 November 2008)
   
   
4. Unpack it and prove UCD_data1, UCD_data2, UCD_proc1, and UCD_proc2 on the CSP_F_v4_1. For example,
   
   
   (1) tar zxvf Uniform_Candy_Distribution_2008.tar.gz
   (2) cd Uniform_Candy_Distribution_2008
   (3) Isabelle -l CSP_F_v4_1      (start Proof General)
   (4) load the files UCD_data1.thy
   (5) prove it by C-c C-n step by step
   (6) similarly, load and prove UCD_data2.thy, UCD_prove1.thy, and UCD_proc2.thy in order.
   
    
   Note: it may take time to complete all the proofs. (e.g. 95 minutes in Pentium-M (1.2GHz)).