


 |
 |
 |
| Featured publications: [36(New!)&35,34,17,24,25,28,30-33] in journals. |
 (2) 2D single free-falling drop merging into a liquid film on solid wall.[6][17]
(2) 2D single free-falling drop merging into a liquid film on solid wall.[6][17]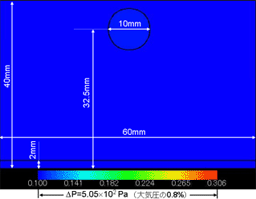 (3) 3D single drop free-falling and merging into a liquid film on solid wall.[6,7,15,21]
(3) 3D single drop free-falling and merging into a liquid film on solid wall.[6,7,15,21]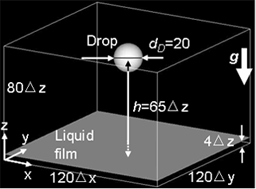
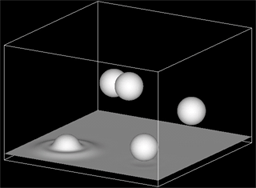 (5) 3D free-falling drops collapsing with vertical liquid film.[6,7,9-12]
(5) 3D free-falling drops collapsing with vertical liquid film.[6,7,9-12]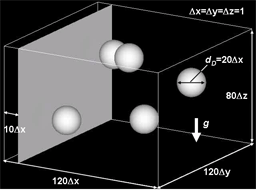 (6) 3D motion of single drop on a flat surface of solid wall with heterogeneous wettability.[6][7]
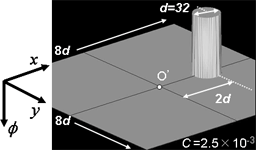
(6) 3D motion of single drop on a flat surface of solid wall with heterogeneous wettability.[6][7]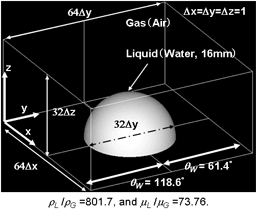 (7) Collapse of liquid column on a flat solid wall in a stagnant gas under gravity.[7,15,16,18,21]
(7) Collapse of liquid column on a flat solid wall in a stagnant gas under gravity.[7,15,16,18,21]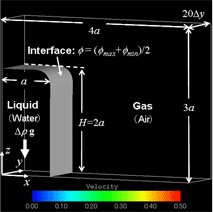 (8) Collapse of 2D liquid column on a flat solid wall in a stagnant gas under gravity.[7,15,16,18,21]
(8) Collapse of 2D liquid column on a flat solid wall in a stagnant gas under gravity.[7,15,16,18,21] [ GIF movie, 1.0MB ]
(9) 2D bubble nucleation on a flat heater in a van-der-Waals fluid.[7][22]
[ GIF movie, 1.0MB ]
(9) 2D bubble nucleation on a flat heater in a van-der-Waals fluid.[7][22]zoom.gif) (10) Deformation and breakup of a single drop in a uniform shear flow at Ca=0.3, Re=0.75 [9]-[12] by Lattice Boltzmann Method(LBM) [13][14].
(10) Deformation and breakup of a single drop in a uniform shear flow at Ca=0.3, Re=0.75 [9]-[12] by Lattice Boltzmann Method(LBM) [13][14]._case0e(Ca03_Re075).gif) [ MPEG1, 333KB ]
[ MPEG1, 333KB ] _case_5(Ca03_Re1)2.gif) [ MPEG1, 929KB ]
[ MPEG1, 929KB ].gif) [ MPEG1, 1.22MB ]
[ MPEG1, 1.22MB ]grid_t=0to20000int1000dt.gif) [ GIF animation, 920KB ]
[ GIF animation, 920KB ].gif) [WMV, 506KB]
[WMV, 506KB]10000steps.gif)
[1] Anderson, D. M.; McFadden, G. B.; Wheeler, A. A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, Vol. 30, p. 139-165. [ doi:10.1146/annurev.fluid.30.1.139 ][Abstract]
[2] Cahn, J. W.; Hilliard, J. E. Free energy of a nonuniform system I. Interfacial free energy. J. Chem. Phys. 1958, Vol. 28, No. 2, p. 258-267. [ doi:10.1063/1.1744102 ][Abstract]
[3] Jacqmin, D. Calculation of Two-Phase Navier-Stokes Flows Using Phase-Field Modeling. J. Comput. Phys. 1999, Vol. 155, No. 1, p. 96-127. [ doi:10.1006/jcph.1999.6332 ][Abstract]
[4] Jamet, D.; Lebaique, O.; Coutris, N.; Delhaye, J. M. The Second Gradient Method for the Direct Numerical Simulation of Liquid-Vapor Flows with Phase Change. J. Comput. Phys. 2001, Vol. 169, No. 2, p. 624-651. [ doi:10.1006/jcph.2000.6692 ][Abstract]
[5] Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys. 2004, Vol. 198, No. 2, p. 628-644. [ doi:10.1016/j.jcp.2004.01.019 ][Abstract]
[6] Takada, N.; Tomiyama, A. A Numerical Method for Two-Phase Flow Based on a Phase-Field Model. Transactions of the Japan Society of Mechanical Engineers, Series B ( Trans. Jpn. Soc. Mech. Eng. Ser. B ). 2005, Vol. 71, No. 701, Paper No. 04-0186, p. 117-124 (in Japanese). [ doi:10.1299/kikaib.71.117 ][CiNii][Abstract][Text(Image PDF)] [ Update on May 15, 2013 ]
[7] Takada, N.; Misawa, M.; Tomiyama, A. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Proceedings of 2005 ASME Fluids Engineering Division Summer Conference. CD-ROM, Paper No. FEDSM2005-77367, June 19-23, 2005, Houston, Texas, USA. [ doi:10.1115/FEDSM2005-77367 ][Abstract][Text(PDF,Local)] [ Update on May 20, 2013 ]
[8] Seta, T.; Kono, K. Thermal Lattice Boltzmann Method for Liquid-Gas Two-Phase Flows in Two Dimensions. JSME International Journal Series B - Fluids and Thermal Engineering ( JSME Int. J. Ser. B-Fluids Therm. Eng. ). 2004, Vol. 47, No. 3, p. 572-583. [ doi:10.1299/jsmeb.47.572 ][Abstract] [ Update on May 15, 2013 ]
[9] Takada, N.; Tomiyama, A.; Hosokawa, S. Lattice Boltzmann Simulation of Interfacial Deformation. International Journal of Modern Physics B ( Int. J. Mod. Phys. B ). 2003, Vol. 17, Nos. 1-2, p. 179-182. [ doi:10.1142/S0217979203017308 ][Abstract]
[10] Takada, N.; Tomiyama, A.; Hosokawa, S. Lattice Boltzmann Simulation of Drops in a Shear Flow. Proc. 4th ASME-JSME Joint Fluids Engineering Conference. CD-ROM, Paper No. FEDSM2003-45166, Honolulu, Hawaii, USA, July 6-10, 2003. [ doi:10.1115/FEDSM2003-45166 ][Abstract] [ Update on May 20, 2013 ]
[11] Takada, N.; Tomiyama, A.; Hosokawa, S. Numerical Simulation of Drops in a Shear Flow by a Lattice-Boltzmann Binary Fluid Model. Computational Fluid Dynamics JOURNAL. 2003, Vol. 12, No. 3, p. 475-481. [Title]
[12] Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Motion of Drops in a Shear Flow Using a Statistical-Thermodynamic Interface Model. Transactions of the Japan Society of Mechanical Engineers, Series B ( Trans. Jpn. Soc. Mech. Eng. Ser. B ). 2004, Vol. 70, No. 699, Paper No.04-0121, p. 2712-2720 (in Japanese). [ doi:10.1299/kikaib.70.2712 ][Abstract][CiNii] [ Update on May 20, 2013 ]
[13] Takada, N.; Misawa, M.; Tomiyama, A.; Fujiwara, S. Numerical Simulation of Two- and Three-Dimensional Two-Phase Fluid Motion by Lattice Boltzmann Method. Computer Physics Communications ( Comput. Phys. Commun. ). 2000, Vol. 129, Nos. 1-3, p. 233-246. [ doi:10.1016/S0010-4655(00)00110-7 ][Abstract]
[14] Takada, N.; Misawa, M.; Tomiyama, A.; Hosokawa, S. Simulation of Bubble Motion under Gravity by Lattice Boltzmann Method. Journal of Nuclear Science and Technology ( J. Nucl. Sci. Technol. ). 2001, Vol. 38, No. 5, p. 330-341. [ doi:10.1080/18811248.2001.9715037 ][Abstract][Full Text(PDF)][CiNii] [ Update on May 15, 2013 ]
[15] Takada, N.; Misawa, M.; Tomiyama, A. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Mathematics and Computers in Simulation ( Math. Comput. Simulat. ). 2006, Vol. 72, Nos. 2-6, p. 220-226. [ doi:10.1016/j.matcom.2006.05.006 ][Abstract]
[16] Takada, N.; Tomiyama, A. Interface-Tracking Simulation of Two-Phase Flows by Phase-Field Method. Proceedings of 2006 ASME Joint U.S.-European Fluids Engineering Summer Meeting. CD-ROM, Paper No. FEDSM2006-98536, July 17-20, 2006, Miami, Florida, USA. [ doi:10.1115/FEDSM2006-98536 ][Abstract][ Forum on Advances in Free Surface and Interface Fluid Dynamics ][Text(PDF,Local)] [ Update on May 20, 2013 ]
[17] Takada, N.; Tomiyama, A. A Numerical Method for Two-Phase Flow Based on a Phase-Field Model. JSME International Journal Series B - Fluids and Thermal Engineering ( JSME Int. J. Ser. B-Fluids Therm. Eng. ). 2006, Vol. 49, No. 3, p. 636-644. [ doi:10.1299/jsmeb.49.636 ][List][CiNii][Contents][Abstract][Text(PDF)][Refs.] [ Update on May 15, 2013 ]
[18] Takada, N.; Tomiyama, A. Application of Interface-Tracking Method Based on Phase-Field Model to Numerical Analysis of Free Surface Flow. Theoretical and Applied Mechanics Japan ( Theor. Appl. Mech. Jpn., Proceedings of NCTAM Japan ). 2006, Vol. 55, p. 149-156. [ doi:10.11345/nctam.55.149 ][Contents][Abstract][Text(Image PDF)][Ref.][Cited-by][Full Text(PDF,Local)] [ Update on June 28, 2013 ]
[19] Swift, M. R.; Orlandini, E.; Osborn W. R.; Yeomans, J. M. Lattice Bolztammn Simulations of Liquid-Gas and Binary Fluid Systems. Physical Review E. 1996, Vol. 54, No. 5, p. 5041-5052. [ doi:10.1103/PhysRevE.54.5041 ][Abstract]
[20] Teng, S.; Chen, Y.; Ohashi, H. Lattice Boltzmann Simulation of Multiphase Fluid Flows through the Total Variation Diminishing with Artificial Compression Scheme. International Journal of Heat and Fluid Flow (Int. J. Heat Fluid Fl.). 2000, Vol. 21, p. 112-121. [ doi:10.1016/S0142-727X(99)00068-5 ][Abstract]
[21] Takada, Naoki; Misawa, Masaki; Tomiyama, Akio. A Phase-Field Method for Interface-Tracking Simulation of Two-Phase Flows. Progress in Multiphase Flow Research. 2006, Vol. 1, p. 171-179 (in Japanese). [ doi:10.3811/pmfr.1.171 ][Contents][Absract][Text(PDF)][Refs.] [ Update on May 15, 2013 ]
[22] Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Two-Phase Flows with Phase Change Using a Phase-Field Method. Progress in Multiphase Flow Research. 2007, Vol. 2, p. 173-180. [ doi:10.3811/pmfr.2.173 ][Contents][Absract][Text(PDF)][Refs.] [ Update on May 15, 2013 ]
[23] Takada, Naoki; Tomiyama, Akio. Numerical Simulation of Isothermal and Thermal Two-Phase Flows Using Phase-Field Modeling. International Journal of Modern Physics C ( Int. J. Mod. Phys. C ). 2007, Vol. 18, No. 4, p. 536-545. [ doi:10.1142/S0129183107010772 ][Abstract]
[24] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Ichikawa, Naoki. Application of a Phase-Field Method to the Numerical Analysis of Motions of a Two-phase Fluid with High Density Ratio on a Solid Surface. Journal of Computational Science and Technology. 2008, Vol. 2, No. 2 (Special Issue on Computational Methods for Multiphase Flows) (2008), p. 318-329. [ doi:10.1299/jcst.2.318 ][Contents][Abstract][Full Text(PDF)][Refs.][Preface] [ Update on May 15, 2013 ]
[25] Matsumoto, Junichi; Takada, Naoki. Two-phase flow analysis based on a phase-field model using orthogonal basis bubble function finite element method. International Journal of Computational Fluid Dynamics ( Int. J. Comput. Fluid Dyn. ). 2008, Vol. 22, No. 8, p. 555-568. [ doi:10.1080/10618560802238226 ][Abstract][AIST RRPDB] [ Update on May 15, 2013 ]
[26] Takada, Naoki; Matsumoto, Junichi. Numerical Analysis of Two-phase Fluid Flows Using a Diffuse-interface Model. RIMS Kokyuroku. 2009, Vol. 1638, p. 83-94. [CiNii][JAIRO][Contents][Handle Proxy(Image PDF)][AIST RRPDB] [ Update on May 15, 2013 ]
[27] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. A Diffuse-interface Tracking Method for the Numerical Simulation of Motions of a Two-phase Fluid on a Solid Surface. Proceedings of the 8th International Conference on Multiphase Flow (ICMF2013), Paper ID: ICMF2013-599, May 26-31, 2013, Jeju, Korea. [AIST RRPDB][ Addition on May 20, 2013 ]
[28] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. Phase-field Model-based Simulation of Motions of a Two-phase Fluid on Solid Surface. Journal of Computational Science and Technology. 2013, Vol. 7, No. 2, p. 322-337. (Special Issue on International Computational Mechanics Symposium, 2012 (ICMS2012), Kobe) [ doi:10.1299/jcst.7.322 ][Abstract][AIST RRPDB] [ Update on June 28, 2013 ]
[29] Takada, N.; Matsumoto, J.; Matsumoto, S. Numerical Simulation of Two-phase Fluid Motion in Microchannel Based on Phase-field Model. Proceedings of the 11th World Congress on Computational Mechanics (WCCM XI - ECCM V - ECFD VI), p. 3895-3903, Paper ID: 2182, July 20-25, 2014, Barcelona, Spain. [Program(MS143B)][Abstract][Paper][AIST RRPDB] [ Update on October 9, 2014 ]
[30] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei. A Diffuse-interface Tracking Method for the Numerical Simulation of Motions of a Two-phase Fluid on a Solid Surface. The Journal of Computational Multiphase Flows. 2014, Vol. 6, No. 3, p. 283-298. [ doi:10.1260/1757-482X.6.3.283 ][Contents][Abstract][AIST RRPDB] [ Update on October 11, 2014 ]
[31] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Kurihara, Kazuma. CFD Simulation of Microscopic Two-phase Fluid Motion on Solid Body with Edges and Heterogeneously-wetted Surface Using Phase-field Model. Proceedings of the 6th International Conference on Coupled Problems in Science and Engineering (Coupled Problems 2015), p. 625-634, Paper ID 320, May 18-20, 2015, San Servolo, Venice, Italy. [Program(WeE03)][Abstract(PDF)][Full paper(PDF)][AIST RRPDB] [ Addition on October 5, 2015 ]
[32] Inoue, Yasuhiro; Ishida, Kazuki; Takada, Naoki; Hojo, Masaki. Reductions in anisotropic errors from implementation of phase-field wetting boundary condition for off-grid objects. International Journal of Computational Methods (Int. J. Comput. Meth.). 2015, Vol. 12, No. 6, 1550042. [ doi:10.1142/S0219876215500425 ][Abstract][AIST RRPDB] [ Addition on October 5, 2015 ]
[33] Takada, Naoki; Matsumoto, Junichi; Matsumoto, Sohei; Kurihara, Kazuma. Phase-field model-based simulation of two-phase fluid motion on partially wetted and textured solid surface. Journal of Computational Science (J. Comput. Sci.). 2016, Vol. 17, Part. 2, p. 315-324. [ doi:10.1016/j.jocs.2016.05.009 ][Abstract][Google][AIST RRPDB] [ Addition on January 2, 2017 ]
[34] Aihara, Shintaro; Takaki, Tomohiro; Takada, Naoki. Multi-phase-field modeling using a conservative Allen-Cahn equation for multiphase flow. Computers & Fluids ( Comput. Fluids ). 2019, Vol. 178, p. 141-151. [ doi:10.1016/j.compfluid.2018.08.023 ][Abstract] [ Addition on May 30, 2022 ]
[35] Takada, Naoki; Mogi, Katsuo; Takaki, Tomohiro; Someya, Satoshi; Baba, Soumei; Saito, Shimpei. Microfluidic simulations of droplet motion on structured solid surface using phase-field lattice Boltzmann method. Multiphase Science and Technology ( Multiph. Sci. Technol. ). 2022, Vol. 34, No. 3, p. 17-33. [ doi:10.1615/MultScienTechn.2022043657 ][Abstract] [ Update on November 17, 2022 ]
[36] Aihara, Shintaro; Takada, Naoki; Takaki, Tomohiro. Highly conservative Allen-Cahn-type multi-phase-field model and evaluation of its accuracy. Theoretical and Computational Fluid Dynamics (Theor. Comput. Fluid Dyn.). 2023, Vol. 37, in press. [ doi:10.1007/s00162-023-00655-0 ][Abstract][Full Text(PDF)][Researchmap] [ Addition on July 30, 2023 ]
|
Last Update on July 30, 2023. Copyright © 2001-2023 by Naoki TAKADA (AIST), All Rights Reserved. E-mail (Webmaster): naoki-takada@aist.go.jp Access: |
 |
 |
 |
 |