ハドルテストのデモ
ハドルテストとは、すべての地震計を同じ位置に並べて同時に記録をとり、記録システムの機器特性の一致度合いを確認するテストです.ハドルデータの解析方法はアレイデータ解析のデモの場合とまったく同一ですので、初めてBIDOを用いる方はまずそちらをご一読下さい. seismファイルの設定ですべての地震計を同じ位置に設定するだけで、アレイ解析とまったく同様の手順で解析できます.
例えば、ハドルデータ解析用のデモデータをダウンロードしてBIDO2.0のフォルダの下に解凍し、アレイデータの場合と同様な手順で解析してみて下さい.このデモデータは鳥取大学の野口竜也博士からのご厚意で頂いたもので、Oyo Geospace
Corp. の上下動センサー (HS-1 Geophone) 6台を鳥取大学構内の実験室のコンクリート上に設置し(写真)、アンプSA16、ローパスフィルター(カットオフ周波数30Hz)を通してレコーダes8で記録したものです.


それでは早速、
run.sh demo/HDL0001/param.sh [RETURN KEY].
としてデータ解析にうつりましょう.解析結果は、アレイ解析の場合と同様に、データフォルダの下に作成されるRESULTというフォルダに格納されます.
ハドルテストの描画内容は、
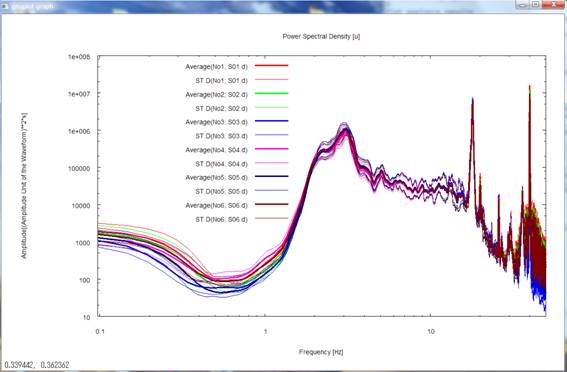
・パワースペクトル密度
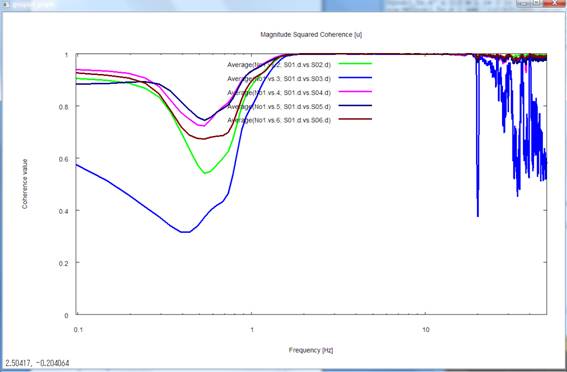
・振幅2乗コヒーレンス
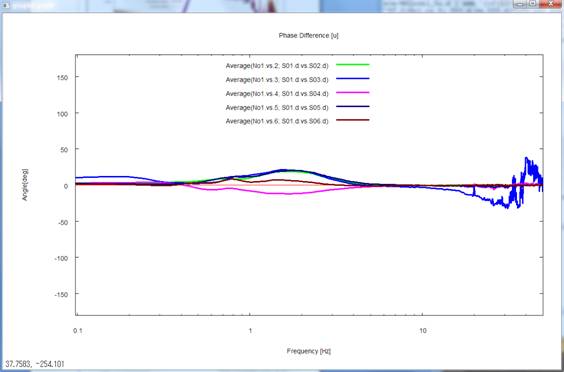
・位相差
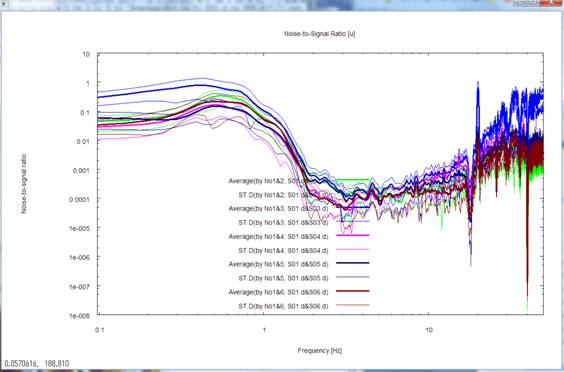
・NS比
・インコヒーレントノイズのパワースペクトル密度
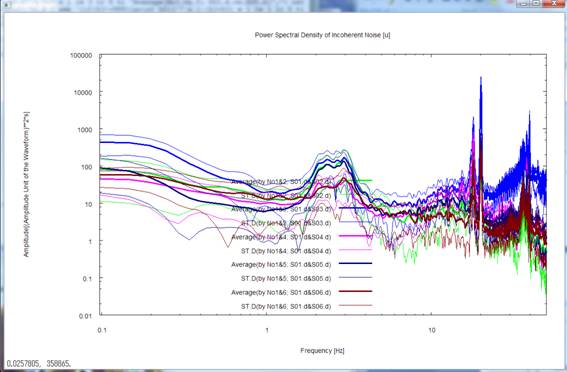
となります.
すべての描画内容は周波数軸を対数目盛にして最大周波数まで表示しています.ここでいう最大周波数とは、\script/\setpar.shのfreqmax_aveというパラメータで設定された値(ディフォルトで50 [Hz].ご自分で変更可です)とナイキスト周波数のうち小さいほうの値のことです.また対数表示をやめたい場合は、\script/\setpar.shのautologscale_xというパラメータの行頭に#を記入してコメントアウトして下さい.
振幅2乗コヒーレンスや位相差の凡例は、Average(by No1.vs. 2;S01.d .vs. S02.d)というふうに表示されています.これは、記録番号1と2の間のコヒーレンス、位相差(1に対して2の位相が進んでいる場合を正)、またそれを用いて計算したNS比やノイズのパワーの平均値という意味です.記録番号1とはseismfileの先頭に書かれたデータに対応します.seismfileのデータ降順に記録番号2、3、...となります.グラフの凡例の「by No1. vs. 2」の部分が記録番号1、2であることを示しています.間違いのないように、その横に「S01.d. vs. S02.d」というふうに、データファイル名も付しています.aveフォルダのave.infoには記録番号とファイル名の対応表が記述されていますので、そちらもご確認下さい.ST.Dは標準偏差(Standard Deviation)を意味しています.上の解析結果より、記録番号3(S03.dの記録;青線)のみコヒーレンスが低く、他の記録に対して位相差が大きいことが分かります.
振幅2乗コヒーレンスの推定や物理的意味についてはBendat and Piersol (1971)やCarter et al.(1973)が参考となります.NS比は振幅2乗コヒーレンス(![]() )を式:
)を式:
![]()
(Carter et al., 1973)に代入してSN比を計算し、その逆数をとりました.ノイズのパワースペクトルは、記録のパワースペクトルにNS比を乗じることにより算出しました.
これらの描画データは、アレイ解析の場合と同様に、RESULT\aveというフォルダに入っています.描画データのファイル名と内容をこちらにリストアップしておきましたので参考にして下さい.そのうちの1つに、DIFINSTRES1_2e.dという名前のファイルがあります.このファイル名はDifferences
in instrumental responseの略です.内容は、記録番号1に対する記録番号2の振幅比と位相差が、
周波数F [Hz] 振幅比R [無次元]
位相差P [°]
というように周波数ごとに列挙されています.このファイルは名前を変えてそのままアレイデータ解析のための機器特性の補正に用いることができます(データの前処理のデモ参照).
Bendat, J. S., and A. G. Piersol, Random Data: Analysis and Measurement
Procedures: John Wiley & Sons, 1971.
Carter, G. C., C. H.
Knapp, and A. H. Nuttall, 1973, Estimation of the
magnitude-squared coherence function via overlapped Fast Fourier Transform
processing: IEEE Transactions on Audio Electroacoustics,
AU-21, 337–344.